Bryły obrotowe - stożek
Stożek to bryła, która powstała w wyniku obrotu trójkąta prostokątnego dookoła prostej zawierającej jedną z przyprostokątnych.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dajy7psdP

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dajy7psdP
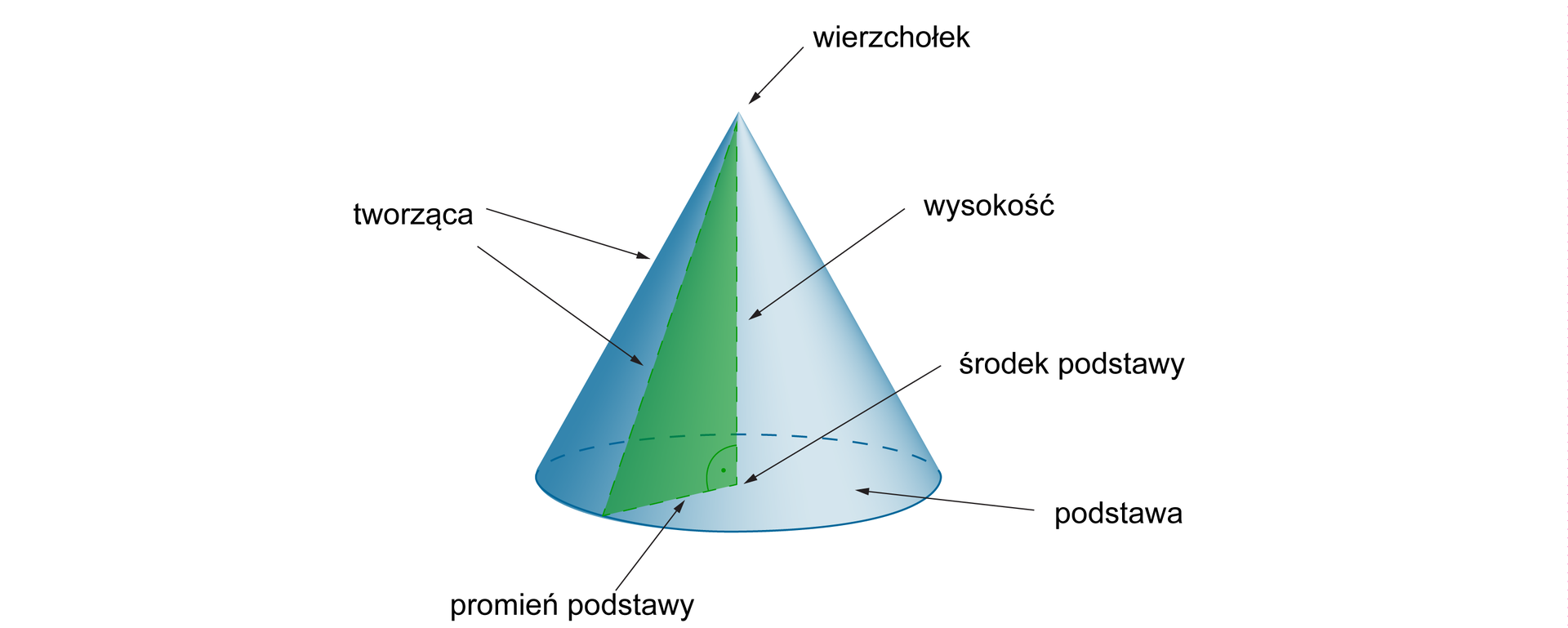
Pole powierzchni całkowitej stożka jest równe:
Objętość stożka jest równa:
Siatka stożka

Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje stojące na drodze pachołki drogowe w kształcie stożka. Kreślone są krawędzie jednego pachołka - powstaje stożek, który następnie rozkłada się na siatkę stożka.
Siatka stożka

Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje siatkę stożka, która następnie składa się w stożek. Stożek zamienia się w pachołek drogowy. Na drodze stoją cztery pachołki.
Trójkąt prostokątny o przyprostokątnych i obraca się wokół dłuższego boku. Oblicz pole powierzchni całkowitej i objętość otrzymanego w ten sposób stożka.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dajy7psdP
Przykrój osiowy stożka jest trójkątem prostokątnym, którego przeciwprostokątna jest równa 8 cm. Oblicz objętość i pole powierzchni bocznej stożka.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dajy7psdP
Pole podstawy stożka jest równe , a jego tworząca jest nachylona do płaszczyzny podstawy pod kątem , takim, że . Oblicz objętość stożka.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dajy7psdP
Oblicz objętość stożka, którego powierzchnia boczna jest wycinkiem koła stanowiącym koła o promieniu .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dajy7psdP
Przekrój osiowy stożka jest trójkątem równobocznym o polu . Oblicz pole powierzchni bocznej i objętość tego stożka.
Trójkąt o przeciwprostokątnej długości obrócono wokół prostej zawierającej jedną z przyprostokątnych. Kąt rozwarcia otrzymanego w ten sposób stożka jest równy Oblicz objętość i pole powierzchni całkowitej tego stożka.
Powierzchnia boczna stożka po rozwinięciu na płaszczyźnie jest półkolem o promieniu . Oblicz objętość stożka.
Koło o średnicy podzielono na dwa wycinki koła w ten sposób, że jeden z nich stanowi drugiego. Z obu wycinków utworzono powierzchnie boczne stożków. Niech oznacza objętość stożka utworzonego z większego wycinka, – objętość stożka utworzonego z mniejszego wycinka. Wyznacz stosunek .
Podstawą stożka jest koło o polu . Pole powierzchni bocznej jest razy większe od pola podstawy. Oblicz sinus kąta nachylenia tworzącej stożka do płaszczyzny podstawy.
Walec i stożek mają równe promienie podstawy i wysokości . Oblicz stosunek pola powierzchni bocznej walca do pola powierzchni bocznej stożka.
Trójkąt prostokątny o przyprostokątnych 3 cm i 4 cm obraca się wokół przeciwprostokątnej. Oblicz objętość otrzymanej w ten sposób bryły.
Stożek o promieniu podstawy i wysokości przecięto płaszczyzną równoległą do podstawy przechodzącą przez środek wysokości stożka. Oblicz stosunek objętości brył na jakie został podzielony stożek.