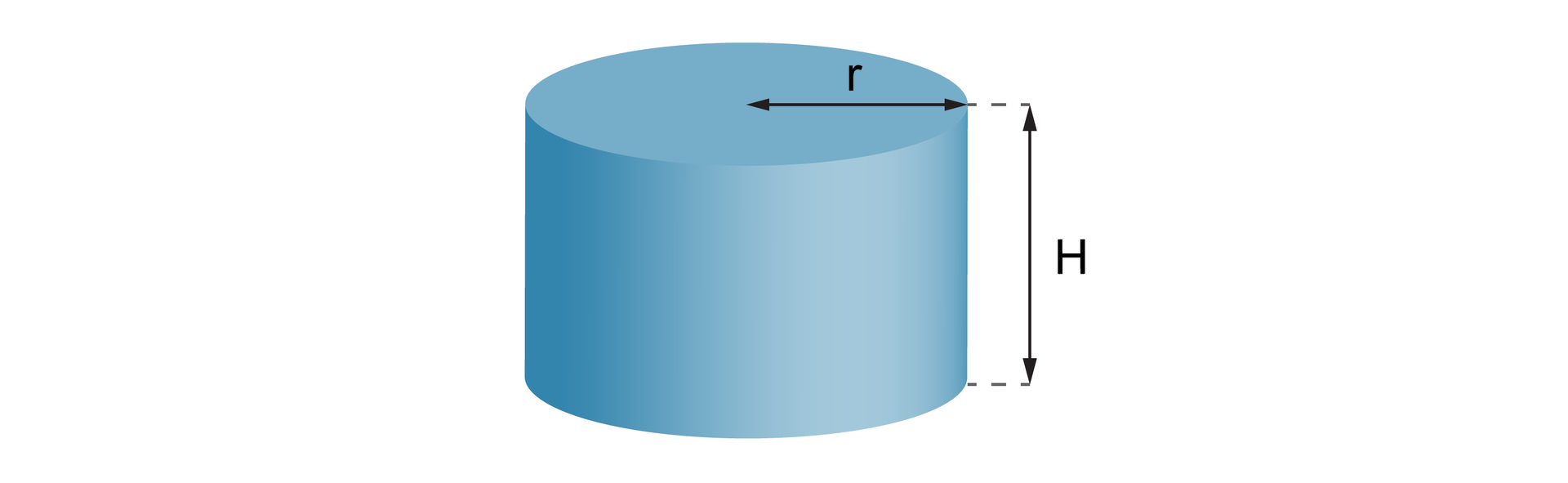
Objętość walca
Wzór na objętość walca
Wyobraź sobie, że pojemnik w kształcie walca o wysokości wypełniamy jednakowymi krążkami o wysokości i promieniu podstawy równym promieniowi podstawy pojemnika.
Ile takich krążków zmieści się w pojemniku?
Jeśli przyjmiemy, że objętość takiego krążka jest równa , to ile wynosi objętość pojemnika?
Jeśli teraz zwiększymy promień podstawy pojemnika i analogicznie promień podstawy krążków, to czy objętość pojemnika zmieni się?
Objętość walca zależy od jego wysokości i pola podstawy. Obliczamy ją podobnie jak objętość graniastosłupa.
Objętość walca o promieniu podstawy jest równa iloczynowi pola podstawy walca przez jego wysokość .
Ile litrów wody mieści się w pojemniku o wysokości i średnicy podstawy ? Przyjmij
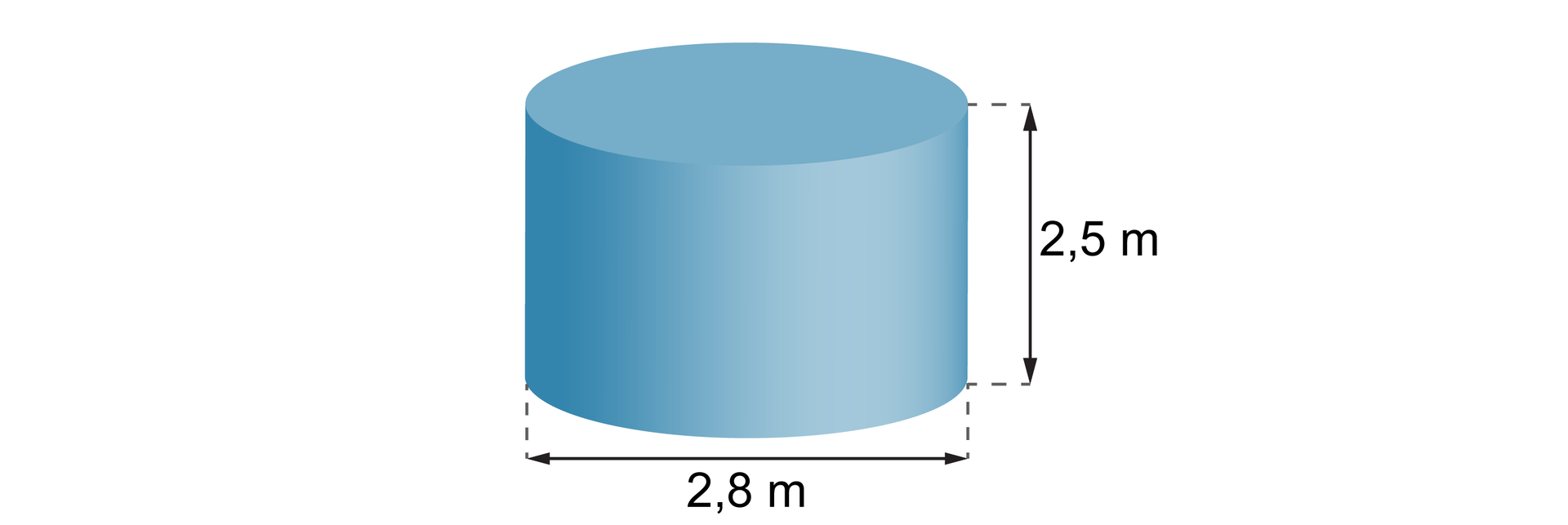
Promień podstawy pojemnika wynosi . Obliczamy objętość walca.
Wiadomo, że , stąd to .
W pojemniku mieści się wody.
Objętość walca przedstawionego na rysunku jest równa .

Oblicz promień podstawy tego walca. Przyjmij .
Korzystamy ze wzoru na objętość walca.
bo
Promień podstawy walca wynosi .
Obliczanie objętości walca

Film dostępny na portalu epodreczniki.pl
Animacja
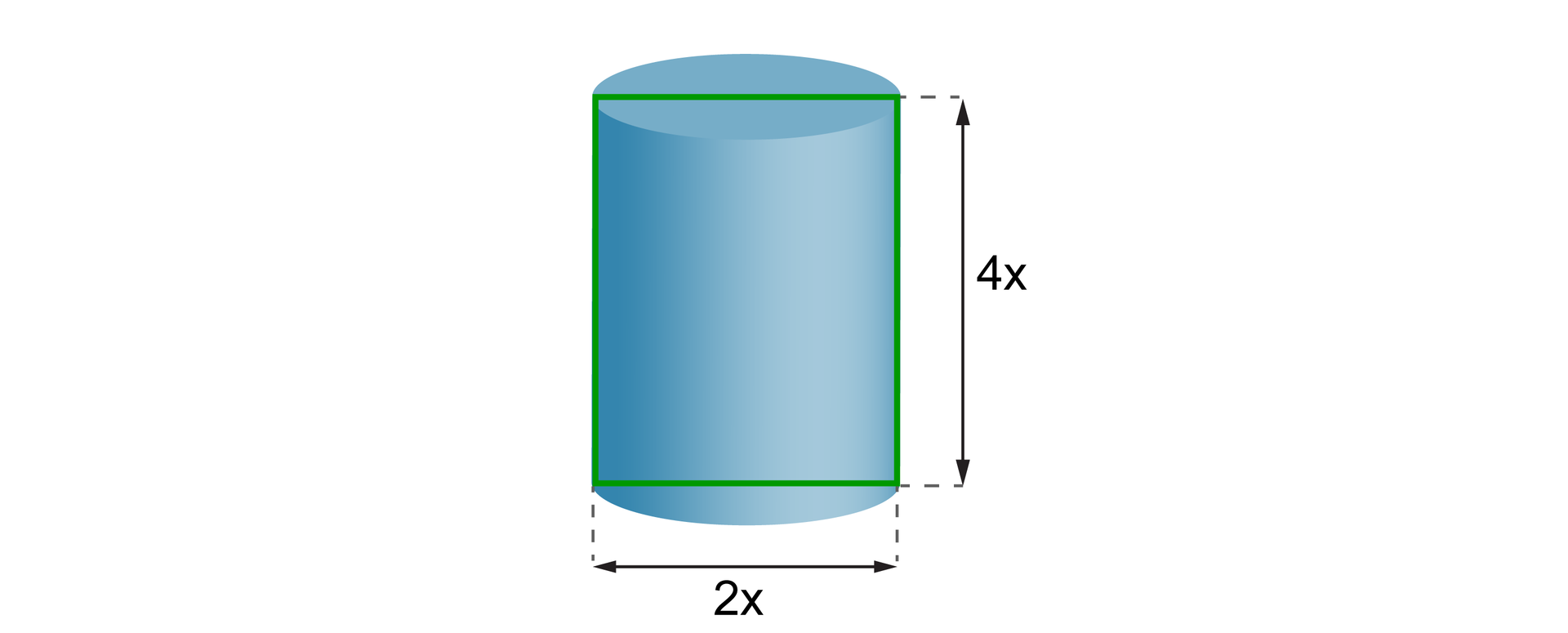
Oblicz objętość walca, którego siatkę przedstawia rysunek. Przyjmij .

Powierzchnia boczna walca po rozwinięciu na płaszczyźnie jest prostokątem, którego długość jest równa obwodowi koła, będącego podstawą walca.
Obliczamy promień tego koła.
Wysokość walca jest równa szerokości prostokąta, czyli .

Obliczamy objętość walca.
Objętość walca jest równa .
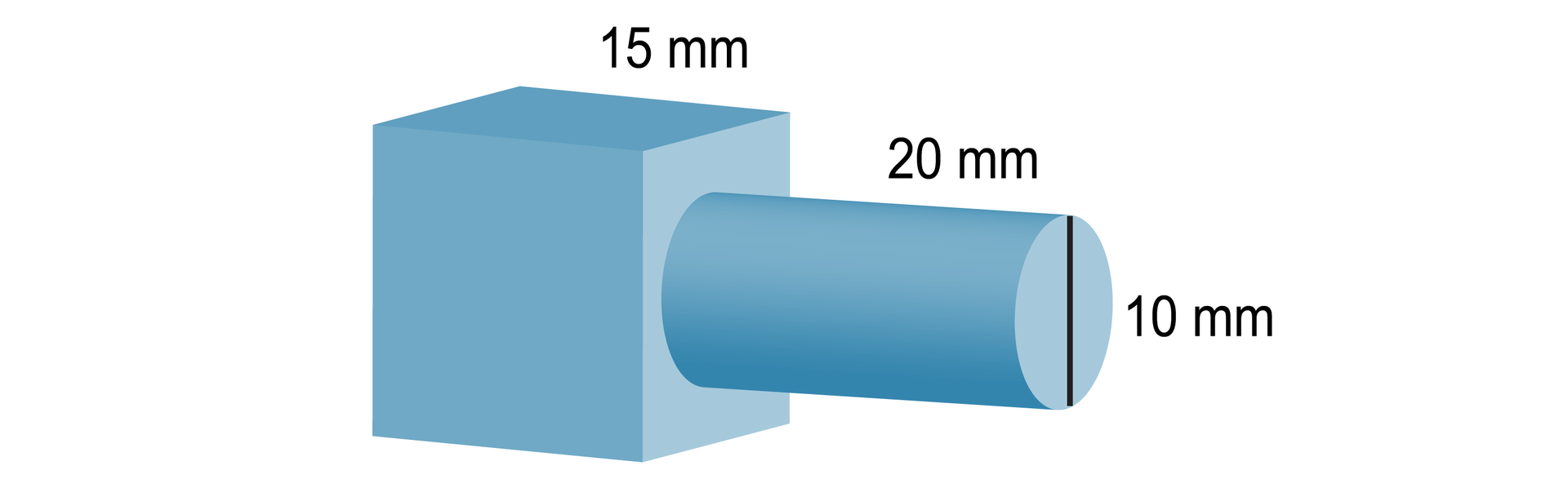
Element przedstawiony na rysunku wykonany jest ze stali o gęstości .

Oblicz masę elementu.
Element jest w kształcie sześciennej kostki z wydrążonym otworem w kształcie walca.
Obliczamy najpierw objętość elementu. Jest ona równa różnicy objętości sześcianu i objętości walca o wysokości i promieniu podstawy .
Masa ciała jest równa iloczynowi objętości tego ciała przez jego gęstość.
Masa elementu wynosi około .
Przekrój osiowy walca jest prostokątem, w którym jeden z boków, równy wysokości walca, jest dwukrotnie dłuższy od drugiego.
Pole powierzchni walca jest równe 250 . Oblicz objętość walca.
Oznaczmy:
– promień podstawy walca w
- wysokość walca w , gdzie .
Wtedy pole powierzchni walca jest równe;
Jednocześnie wiemy, że pole to jest równe .
Promień podstawy walca jest więc równy , a jego wysokość . Obliczamy objętość walca.
Objętość walca jest równa .
Kartkę papieru w kształcie prostokąta o wymiarach na można zwinąć na dwa sposoby,
uzyskując za każdym razem walec. Jeden z nich będzie niższy i grubszy, drugi wyższy i chudszy.
Który w tych walców ma większą objętość?
Poniższy rysunek ilustruje w przybliżeniu kartkę papieru i dwa uzyskane walce.
Przyjmując za i długość i szerokość kartki, wyznaczmy najpierw promień podstawy każdego z walców.

Czy w każdej ze szklanek, jak przedstawiono jak na rysunku, zmieści się ćwierć litra wody? Przyjmij .

Butla gazowa domowa – parametry techniczne
Wysokość zewnętrzna bez zaworu | |
Masa butli | |
Średnica zewnętrzna | |
Średnica wewnętrzna |
Przyjmij, że butla gazowa ma kształt walca. Oblicz jej pojemność. Przyjmij .
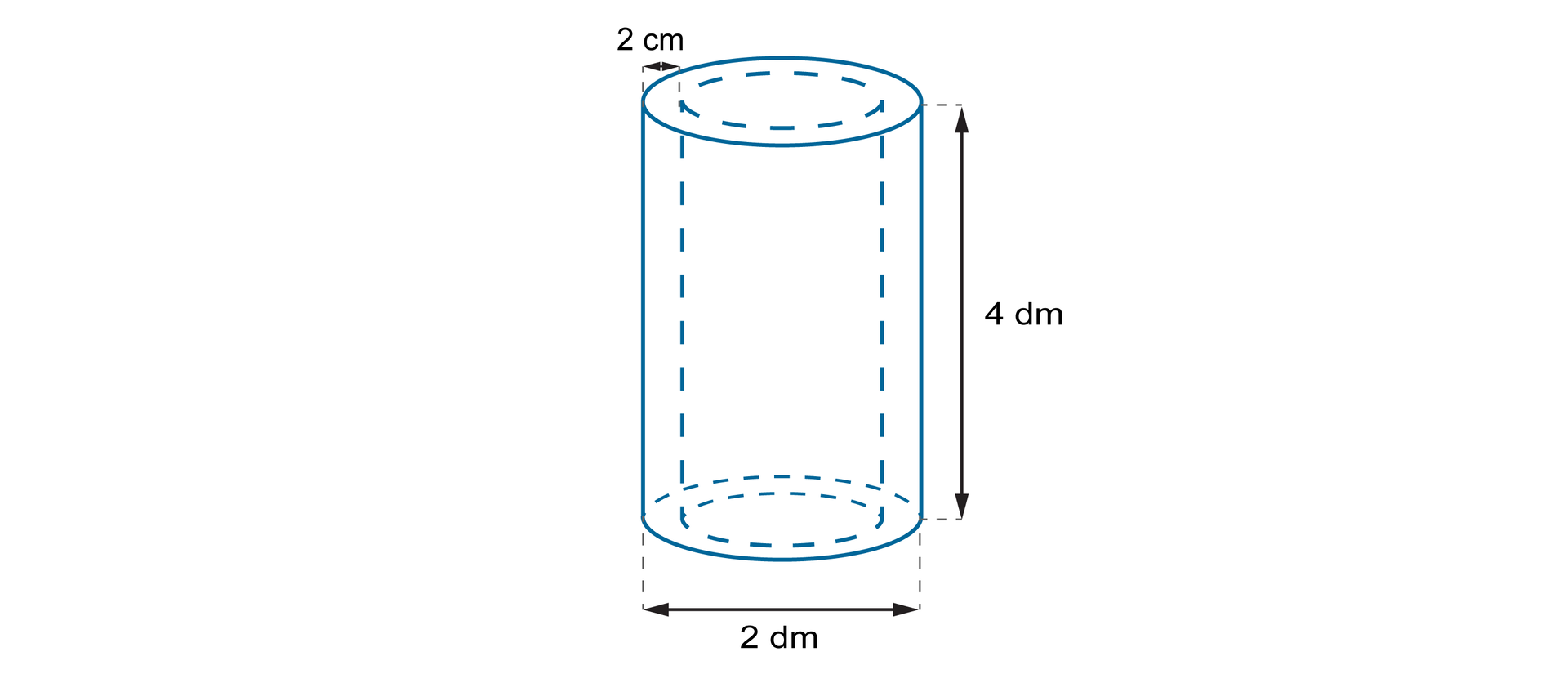
Rurkę, taką jak na rysunku przetopiono i wykonano z niej sześcienną kostkę. Oblicz pole powierzchni tej kostki. Wynik podaj z dokładnością do .
Element betonowy składa się z części w kształcie sześcianu i części w kształcie walca. Ile takich elementów można wykonać z betonu? Przyjmij .
Pojemnik z sokiem jest prostopadłościanem o wymiarach . Sok rozlano do szklanek w kształcie walca o średnicy podstawy i wysokości . Ile szklanek napełniono sokiem? W obliczeniach przyjmij .
Która z brył ma większą objętość - sześcian o krawędzi czy walec o promieniu i wysokości . W obliczeniach przyjmij .
Głównymi składnikami powietrza są azot i tlen. Zawartość procentowa azotu wynosi , a tlenu . Jeden powietrza ma masę . Jaka jest masa azotu, a jaka tlenu w butli w kształcie walca o średnicy dna i wysokości ? W obliczeniach przyjmij .
Walec powstał w wyniku obrotu prostokąta o bokach długości i dookoła krótszego boku. Oblicz objętość walca.
Długości boków prostokąta pozostają w stosunku . Prostokąt obraca się raz wokół dłuższego boku, a raz wokół krótszego boku. Który z tak powstałych walców będzie miał większą objętość i ile razy, a który będzie miał większe pole powierzchni całkowitej i ile razy?
Oblicz pole powierzchni bocznej i objętość walca, którego przekrój osiowy jest kwadratem o polu równym .
Objętość walca jest równa . Wysokość walca jest razy większa od promienia podstawy. Oblicz promień podstawy i wysokość tego walca.
Dwa walce oraz mają jednakowe objętości. Długość promienia podstawy walca jest dziesięciokrotnie mniejsza od długości promienia podstawy walca . Ile razy wysokość walca jest większa od wysokości walca ?
Wysokość walca jest równa promieniowi podstawy tego walca. Objętość walca jest równa . Oblicz pole podstawy tego walca.
Jaką pojemność ma naczynie w kształcie walca o średnicy podstawy i wysokości ?