Odczytywanie danych statystycznych

Film dostępny na portalu epodreczniki.pl
Animacja
Zbieraniem i udostępnianiem informacji na temat większości dziedzin życia publicznego i niektórych stron życia prywatnego zajmuje się Główny Urząd Statystyczny - GUS, którego główna siedziba znajduje się w Warszawie. W Polsce najważniejsze informacje o państwie, jego mieszkańcach, środowisku, gospodarce i zjawiskach społecznych są umieszczone w Roczniku Statystycznym, który wydawany jest przez GUS.
W życiu codziennym spotykamy się również z wieloma informacjami. Dane statystyczne mogą być uzyskiwane w różny sposób: poprzez sondaże, spisy, referenda, wywiady, badania. Przedstawiane są one za pomocą opisu słownego, tabel, wykresów, diagramów. Typ diagramu zależy od rodzaju informacji, jaką chcemy przedstawić.
W pewnym gimnazjum dokonano zestawienia liczby uczniów wszystkich klas pierwszych, drugich oraz trzecich w podziale na dziewczęta i chłopców.
Przeanalizujmy tabelę, diagramy słupkowe oraz pierścieniowe, w których przedstawiono dane dotyczące liczebności poszczególnych grup klasowych.
Klasa | Liczba dziewcząt | Liczba chłopców | Liczba wszystkich uczniów |
Z tabeli można odczytać:
dokładną liczbę dziewcząt i chłopców w poszczególnych klasach,
dokładną liczbę wszystkich uczniów w poszczególnych klasach,
dokładną liczbę dziewcząt i chłopców w szkole,
dokładną liczbę wszystkich uczniów w szkole,
o ile więcej / o ile mniej jest dziewcząt lub chłopców w każdej klasie.
Ryo9L4r9ZKU1O1 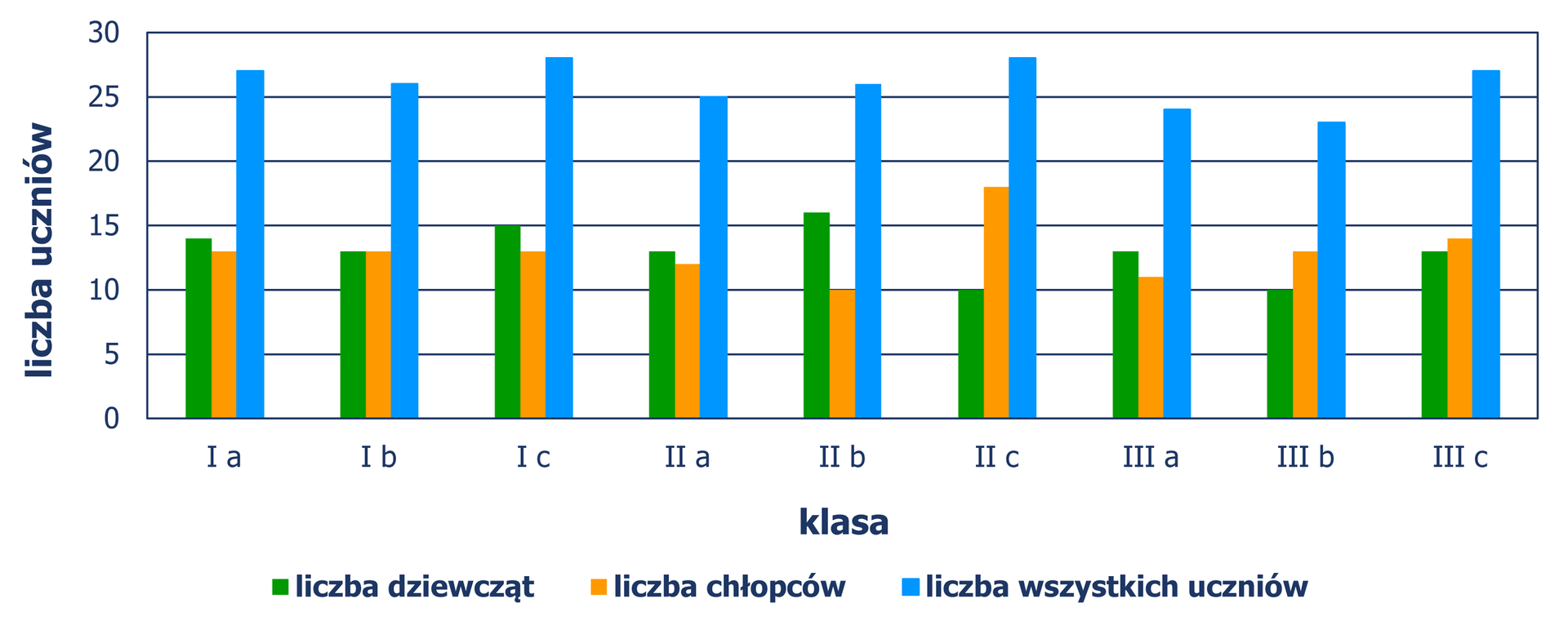 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Z diagramu słupkowego pionowego można odczytać, że:
w klasach liczba dziewcząt jest większa niż liczba chłopców,
w klasach liczba chłopców jest większa niż liczba dziewcząt,
w klasie liczba dziewcząt jest równa liczbie chłopców,
w klasie liczba chłopców jest najmniejsza w szkole,
w klasach liczba dziewcząt jest najmniejsza w szkole,
w klasach liczba wszystkich uczniów jest największa w szkole,
w klasie liczba wszystkich uczniów jest najmniejsza w szkole,
w klasach liczba dziewcząt jest większa niż liczba wyrażająca połowę uczniów tych klas,
największa różnica między liczbą chłopców a liczbą dziewcząt jest w klasie
W diagramach pierścieniowych podano liczbę dziewcząt i liczbę chłopców w poszczególnych klasach.

Z diagramów pierścieniowych można odczytać, że:
w klasie liczba dziewcząt jest największa,
w klasie i liczba dziewcząt jest najmniejsza,
w klasie liczba chłopców jest największa,
w klasie liczba chłopców jest najmniejsza,
w czterech klasach uczy się jednakowa liczba dziewcząt i w czterech klasach uczy się jednakowa liczba chłopców.
Przeanalizujmy tabelę i diagram słupkowy, w których przedstawiono dane dotyczące maksymalnej głębokości jezior w Polsce.
Źródło: Mały Rocznik Statystyczny Polski -rok
Nazwa jeziora (nazwa województwa) | Maksymalna głębokość w metrach |
Hańcza (woj. podlaskie ) | |
Drawsko (woj. zachodniopomorskie) | |
Wielki Staw (woj. małopolskie) | |
Czarny Staw (woj. małopolskie) | |
Wigry (woj. podlaskie ) | |
Wdzydze (woj. pomorskie) | |
Wuksniki (woj. warmińsko‑mazurskie) | |
Babięty Wlk. (woj. warmińsko‑mazurskie) | |
Morzycko (woj. zachodniopomorskie) |
Z tabeli można odczytać:
dokładną maksymalną głębokość każdego z wymienionych jezior podaną w metrach,
nazwę województwa, w którym dane jezioro się znajduje.
W diagramie słupkowym na osi pionowej zaznaczone zostały nazwy jezior, a na osi poziomej wartości liczbowe, które określają maksymalną głębokość jeziora wyrażoną w metrach.

Z diagramu słupkowego poziomego można odczytać, że:
najgłębszym jeziorem w Polsce jest Hańcza,
zbliżoną głębokość mają jeziora Drawsko i Wielki Staw oraz Wdzydze i Wuksniki,
głębokość większą niż metrów i mniejszą niż metrów mają cztery jeziora: Drawsko, Wielki Staw, Czarny Staw, Wigry,
głębokość większą niż maksymalna głębokość jeziora Wigry mają cztery jeziora: Hańcza, Drawsko, Wielki Staw, Czarny Staw.
Przeanalizujmy tabelę łodygowo‑listkową i diagramy procentowe, w których przedstawiono dane dotyczące wzrostu pewnej grupy osób.
Wzrost uczniów w centymetrach | |
Podczas odczytywania danych z takiej tabeli dwie pierwsze cyfry z pierwszej kolumny traktujemy jako „łodygę”, natomiast cyfry z drugiej kolumny traktujemy jako „listki”.
W tabeli tej zapisano, że wśród badanej grupy osób są osoby o następującym wzroście:
, .
Z tabeli łodygowo‑listkowej można odczytać, że:
grupa liczyła osób,
najniższa osoba ma wzrostu, a najwyższa
trzy osoby mają wzrostu,
dwie osoby mają wzrostu.
W diagramie kołowym podano, jaki procent łącznej liczby badanej grupy stanowią osoby z następujących kategorii: Diagram kołowy, w którym zamiast wartości liczbowych występują wartości procentowe, nazywamy diagramem procentowym.
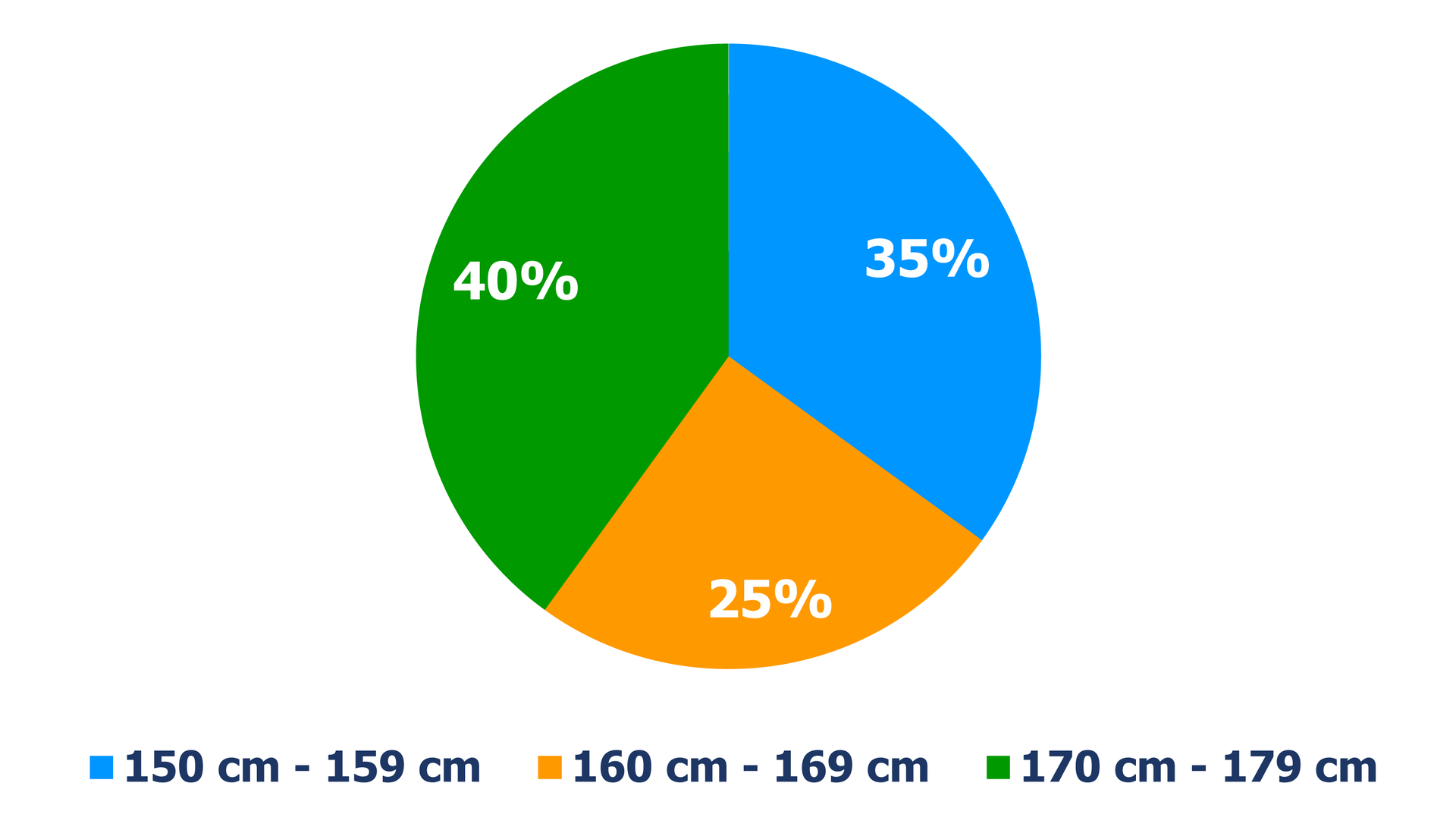
Z diagramu kołowego można odczytać, że:
wszystkich osób stanowią osoby, których wzrost należy do kategorii ,
wszystkich osób stanowią osoby, których wzrost należy do kategorii ,
wszystkich osób stanowią osoby, których wzrost należy do kategorii ,
najliczniejszą grupą osób jest grupa, której wzrost należy do kategorii
wszystkich osób stanowią osoby, których wzrost należy do kategorii .
W tabeli przedstawiono dane dotyczące zbiorów owoców, wyrażone w tysiącach ton, w latach
Źródło: Mały Rocznik Statystyczny Polski -
Zbiory owoców z drzew w tym: | |||
Jabłka | |||
Gruszki | |||
Śliwki | |||
Wiśnie | |||
Czereśnie |
W przypadku których owoców pojawił się spadek w zbiorach w latach ?
W przypadku których owoców zaobserwowano największy, a w przypadku których najmniejszy wzrost w zbiorach w latach , oraz w latach ?
W przypadku których owoców oraz w jakich latach nie zaobserwowano zmian w zbiorach?
Podaj największą i najmniejszą różnicę w zbiorach owoców w latach .
Na diagramie przedstawiono wyniki pomiaru masy ciała pewnej liczby dziewcząt i chłopców w wieku lat.

Jak liczna była grupa dziewcząt, a jak liczna grupa chłopców?
Jaka masa ciała występowała najczęściej i najrzadziej wśród dziewcząt?
Jaka masa ciała występowała najczęściej i najrzadziej wśród chłopców?
Ile osób wśród badanych siedmiolatków miało masę ciała poniżej ?
Ilu chłopców miało masę ciała co najmniej równą ?
Jaki procent wszystkich dziewcząt stanowiły dziewczęta, których masa ciała była mniejsza niż ?
Jaki procent wszystkich osób stanowiły osoby, których masa ciała była większa niż ?
O ile procent liczba chłopców o masie ciała większej niż i mniejszej niż była większa niż liczba dziewcząt o tej samej masie ciała?
Na diagramie przedstawiono wyniki sondażu, który został przeprowadzony wśród przechodniów ulicy Spacerowej na temat znaków zodiaku.

Ilu przechodniów wzięło udział w sondażu?
Który znak zodiaku pojawiał się w odpowiedziach przechodniów najczęściej, a który najrzadziej?
Które znaki zodiaku uzyskały jednakową liczbę odpowiedzi w sondażu?
Jaki procent wszystkich przechodniów stanowią osoby spod znaku Panny, a jaki spod znaku Ryby? Wynik podaj z dokładnością do .
Jaki procent odpowiedniego znaku zodiaku stanowi Twój znak zodiaku? Wynik podaj z dokładnością do .
Na diagramie przedstawiono dane dotyczące prędkości rozchodzenia się dźwięku w różnych ośrodkach.

W którym ośrodku dźwięk rozchodzi się najszybciej, a w którym najwolniej?
W których ośrodkach prędkość rozchodzenia się dźwięku jest około razy mniejsza od prędkości, jaką osiąga w diamencie?
Ile razy mniejsza jest prędkość rozchodzenia się dźwięku w ołowiu w porównaniu z aluminium?
O ile procent większa jest prędkość rozchodzenia się dźwięku w szkle od prędkości rozchodzenia się dźwięku w betonie? Wynik zaokrąglij do .
Na diagramie przedstawiono dane dotyczące gęstości różnych pierwiastków chemicznych.
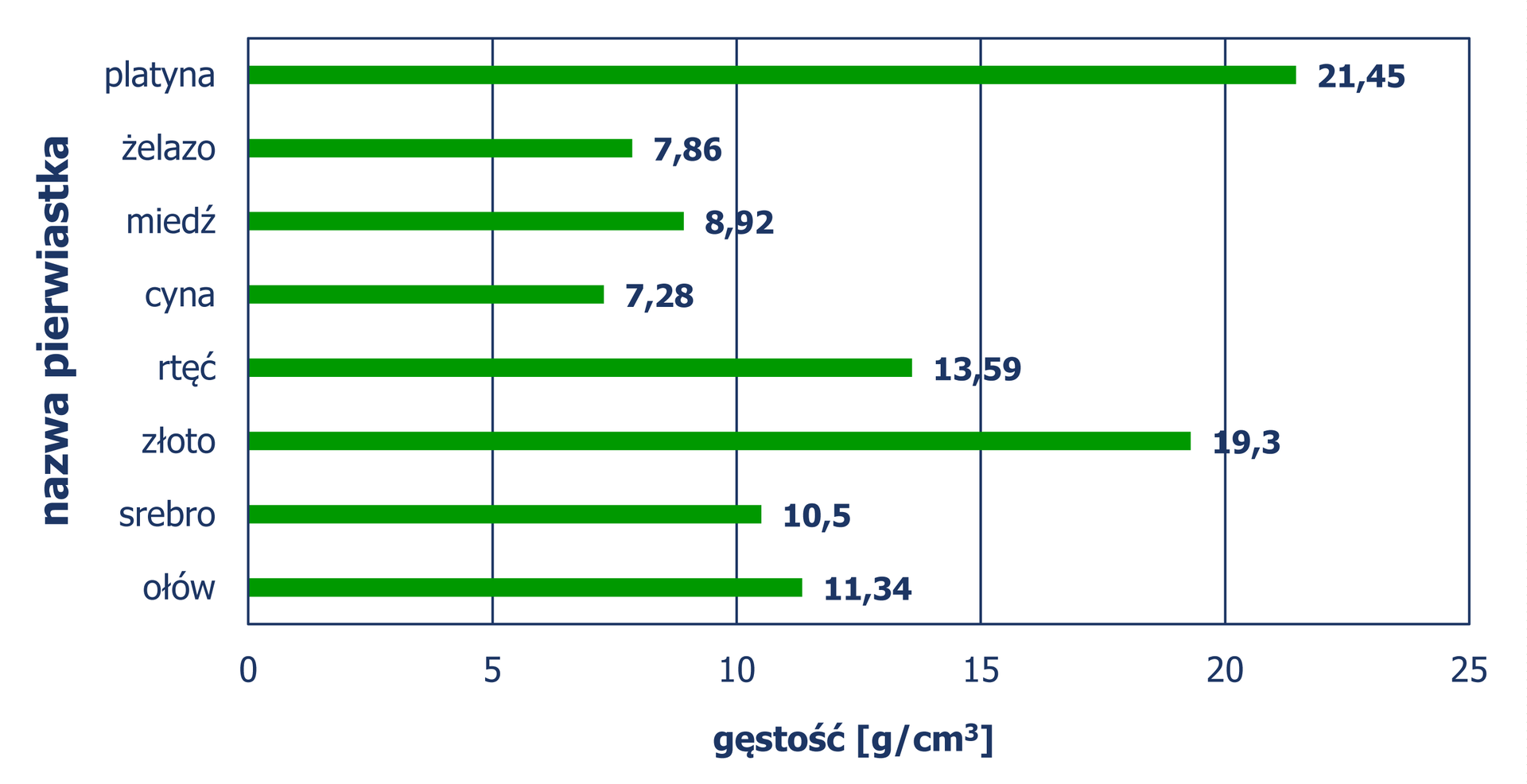
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
Na diagramie przedstawione są dane dotyczące temperatury topnienia i wrzenia niektórych substancji.

Oceń, czy podane zdania są prawdziwe, czy fałszywe.
- Temperatura topnienia wody jest równa
- Temperatura topnienia dla substancji ma ujemną wartość.
- Temperatura wrzenia dla substancji ma dodatnią wartość.
- Najmniejszą różnicę między temperaturą topnienia i wrzenia ma azot
- Największą różnicę między temperaturą topnienia i wrzenia ma złoto.
- Najmniejszą różnicę między temperaturą topnienia i wrzenia ma azot.
- Największą różnicę między temperaturą topnienia i wrzenia ma złoto.
- Największą różnicę między temperaturą topnienia i wrzenia ma azot.
- Najmniejszą różnicę między temperaturą topnienia i wrzenia ma tlen.
- Najmniejszą dodatnią temperaturę wrzenia ma sód.
- Największą dodatnią temperaturę topnienia ma woda.
- Największą ujemną temperaturę wrzenia ma ozon.
- Najmniejszą ujemną temperaturę topnienia ma rtęć.
Na diagramie przedstawiono dane, wyrażone w procentach, które dotyczą sposobów wykorzystania Internetu przez osoby w wieku lata.
Źródło: Mały Rocznik Statystyczny Polski - rok
Ponad osób w wieku w wykorzystywało Internet do:
- korzystania z poczty elektronicznej
- wyszukiwania informacji dotyczących zdrowia, wyszukiwania informacji o towarach i usługach, zakupu towarów i usług
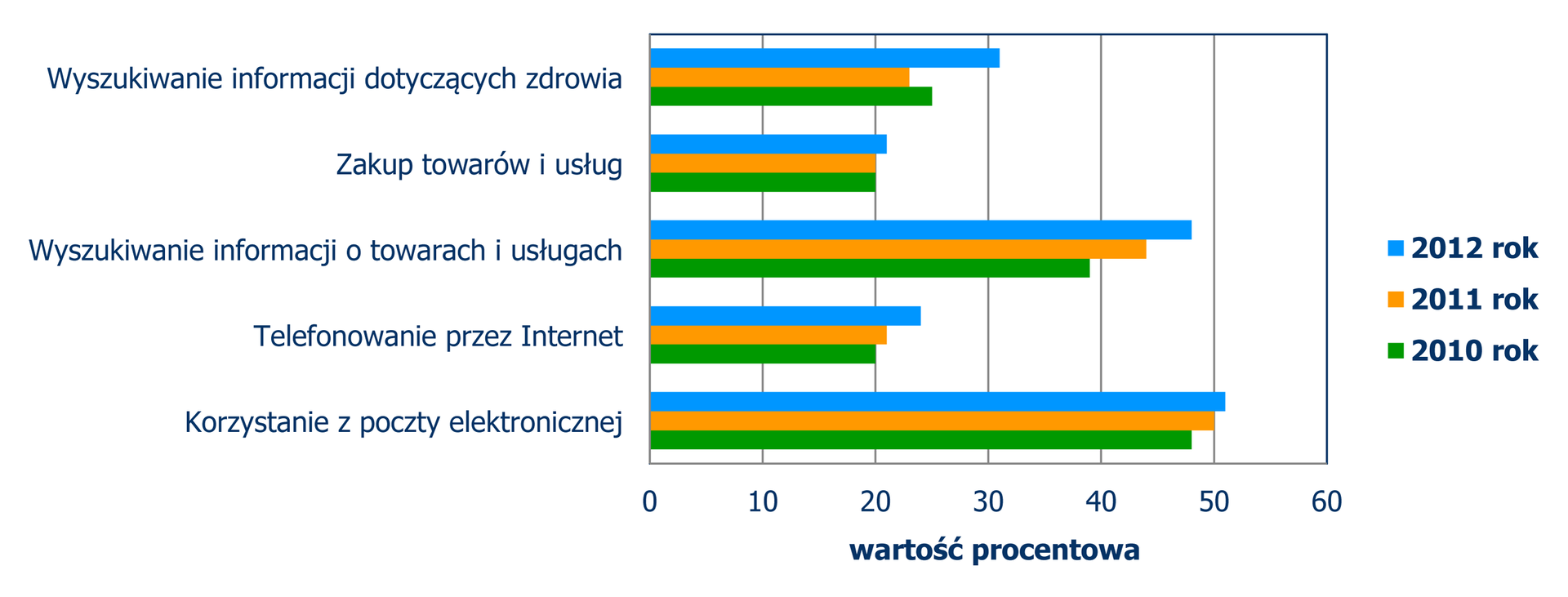
Na diagramie przedstawiono dane, wyrażone w procentach, które dotyczą sposobów wykorzystania Internetu przez osoby w wieku lata.
Źródło: Mały Rocznik Statystyczny Polski - rok

W latach zaobserwowano najbardziej zauważalny wzrost dla
- wyszukiwania informacji o towarach i usługach
- telefonowania przez Internet, zakupu towarów i usług, korzystania z poczty elektronicznej
Na diagramie przedstawiono dane, wyrażone w procentach, które dotyczą sposobów wykorzystania Internetu przez osoby w wieku lata.
Źródło: Mały Rocznik Statystyczny Polski - rok

Korzystanie z poczty elektronicznej w roku było większe
- o punktów procentowych niż zakup towarów i usług
- o niż zakup towarów i usług
- o punktów procentowych niż telefonowanie przez Internet
- o niż telefonowanie przez Internet
Na diagramie przedstawiono dane, wyrażone w procentach, które dotyczą sposobów wykorzystania Internetu przez osoby w wieku lata.
Źródło: Mały Rocznik Statystyczny Polski - rok

W latach zaobserwowano największy wzrost dla
- wyszukiwania informacji dotyczących zdrowia
- telefonowania przez Internet
- wyszukiwania informacji o towarach i usługach
- korzystania z poczty elektronicznej
Na diagramie przedstawiono dane dotyczące średnich temperatur powietrza w ciągu pewnego tygodnia w marcu.
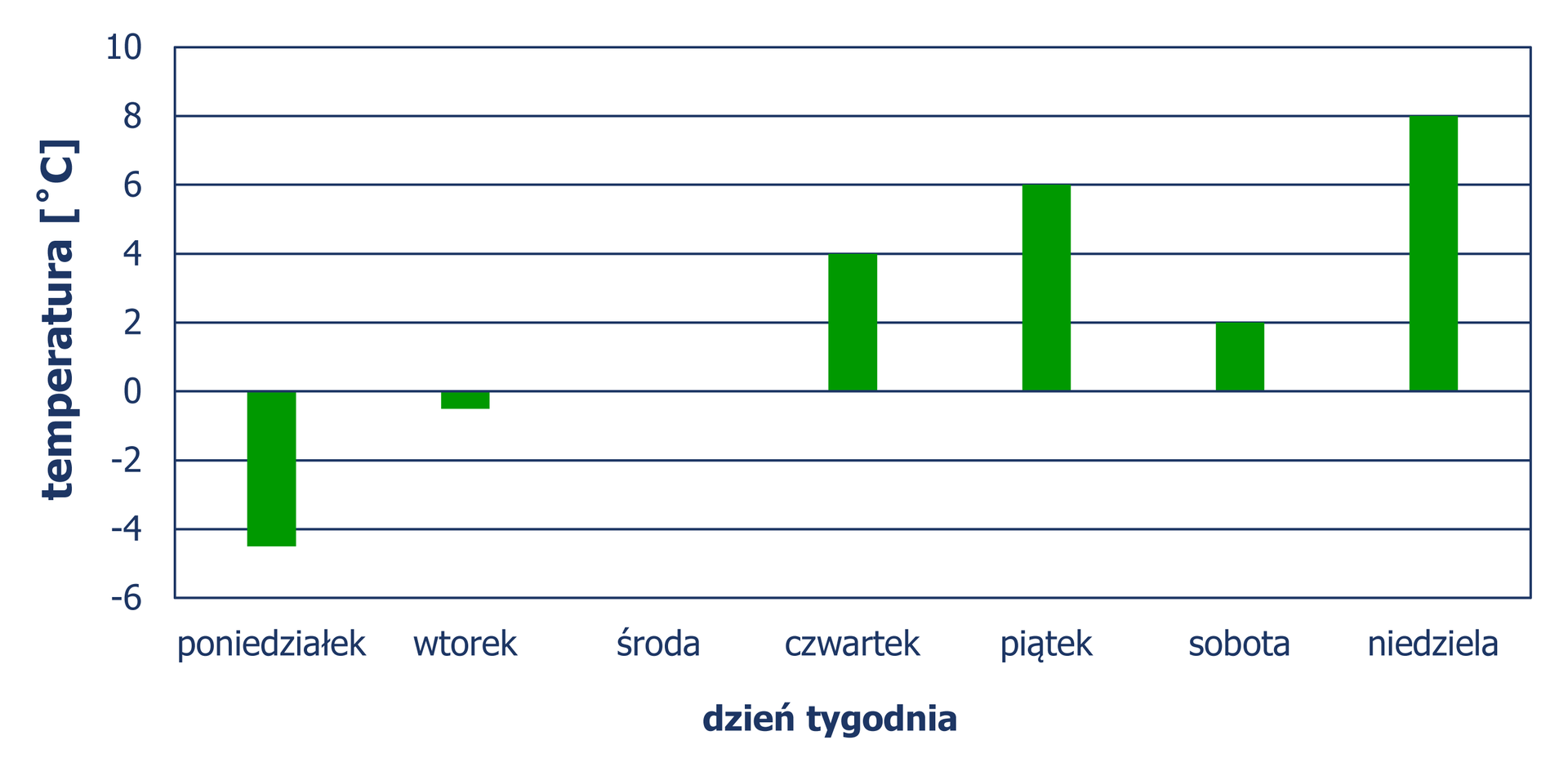
Oceń, czy podane zdania są prawdziwe, czy fałszywe.
- Najwyższa temperatura powietrza była w niedzielę.
- Najniższa temperatura powietrza była w poniedziałek.
- Różnica między najwyższą, a najniższą temperaturą powietrza wynosi
- W sobotę temperatura powietrza zmalała o w porównaniu z piątkiem.
- W piątek temperatura powietrza wzrosła o w porównaniu z temperaturą jaka była w czwartek.
- We wtorek temperatura powietrza wzrosła o w porównaniu z poniedziałkiem.
- W ciągu całego tygodnia widoczny był wzrost temperatury powietrza
- Różnica między najwyższą, a najniższą dodatnią temperaturą powietrza wynosi
- W niedzielę temperatura powietrza była o wyższa niż poprzedniego dnia.
- W sobotę temperatura powietrza była o niższa niż w niedzielę.
- W czwartek temperatura powietrza była niższa niż w pozostałe dni tygodnia.
- Od środy temperatura powietrza była dodatnia.
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Ilu uczniów wzięło udział w ankiecie?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Ile dziewcząt wzięło udział w ankiecie?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Ilu chłopców wzięło udział w ankiecie?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Ile godzin dziennie na odrabianie prac domowych przeznacza najliczniejsza grupa uczniów?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Ile godzin dziennie na odrabianie prac domowych przeznacza grupa uczniów, w której liczba dziewcząt jest trzy razy większa od liczby chłopców?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Ile godzin dziennie na odrabianie prac domowych przeznacza grupa uczniów, w której liczba chłopców jest o jeden większa od liczby dziewcząt?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

O ile procent mniej chłopców niż dziewcząt przeznacza na odrabianie prac domowych cztery godziny dziennie?
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

O ile procent więcej dziewcząt niż chłopców wzięło udział w ankiecie?
- około
- około
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnego gimnazjum. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”

Jaki procent łącznej liczby dziewcząt stanowi łączna liczba chłopców w grupach, gdzie liczba dziewcząt jest mniejsza niż liczba chłopców?
W tabeli przedstawiono dane dotyczące liczby lokatorów i mieszkań w pewnym bloku.
Liczba mieszkań | ||||||
Liczba lokatorów | ||||||
w tym dzieci |
Ile jest wszystkich mieszkań w tym bloku?
Ile jest mieszkań zajmowanych przez lokatorów?
Ile osób dorosłych mieszka w tym bloku?
Ile jest mieszkań zamieszkiwanych również przez dzieci?
Ile dzieci mieszka w tym bloku?
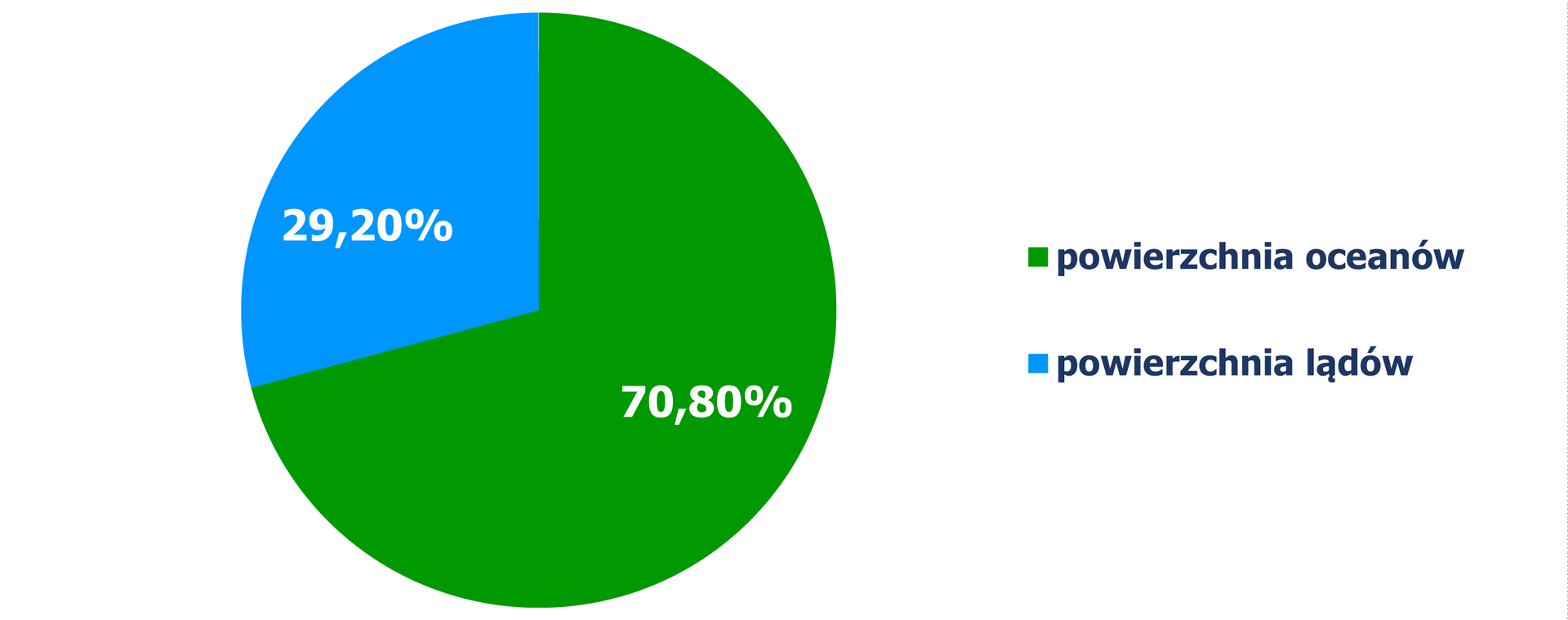
Diagram kołowy przedstawia procentowy podział powierzchni lądów i oceanów na Ziemi.
Źródło: Świat w liczbach
Na diagramach słupkowych przedstawiono dane dotyczące powierzchni poszczególnych kontynentów i oceanów wyrażone w milionach kilometrów kwadratowych.

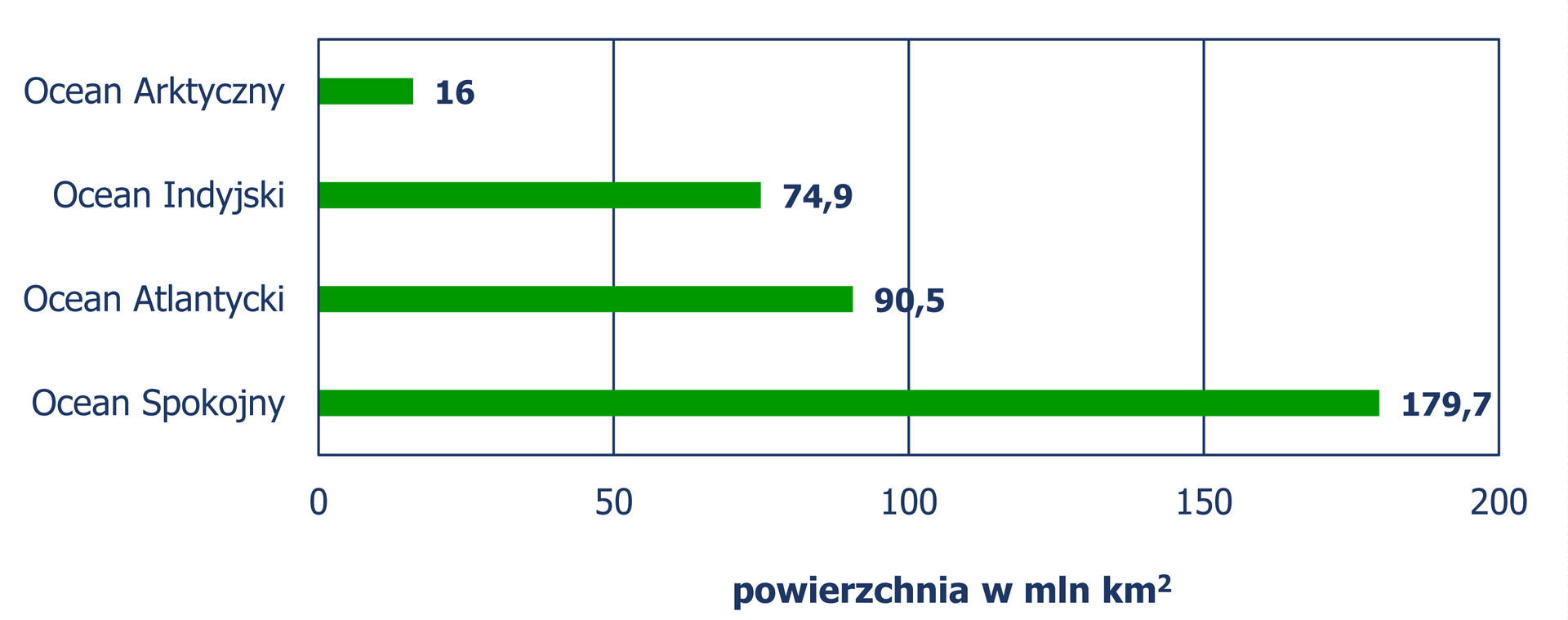
Jaką łączną powierzchnię zajmują kontynenty na Ziemi?
Jaką łączną powierzchnię zajmują oceany na Ziemi?
Jaki procent powierzchni lądów na Ziemi stanowi powierzchnia Afryki, a jakim Europy? Wynik podaj z dokładnością do
O ile procent powierzchnia Azji jest większa niż powierzchnia Antarktyki? Wynik podaj z dokładnością do
Jaki procent powierzchni oceanów na Ziemi stanowi powierzchnia Oceanu Arktycznego? Wynik podaj z dokładnością do
O ile procent powierzchnia Oceanu Atlantyckiego jest mniejsza niż powierzchnia Oceanu Spokojnego? Wynik podaj z dokładnością do