Jak obliczamy ciepło potrzebne do zmiany temperatury, stopienia lub wyparowania ciała?
Jest wiosenny słoneczny dzień, temperatura wynosi +5°C, a na jeziorze ciągle leży gruba warstwa lodu. Dlaczego cały lód nie topi się od razu, gdy tylko temperatura wzrośnie powyżej zera?

podać definicję energii wewnętrznej;
zauważyć, że wzrost temperatury ciała oznacza wzrost jego energii wewnętrznej;
wymienić podstawowe stany skupienia materii oraz nazwy procesów prowadzących do zmiany stanu skupienia.
ustalać, czy ciało pobiera, czy oddaje energię w procesie ogrzewania, stygnięcia, topnienia, krzepnięcia, parowania i skraplania;
podawać definicje ciepła właściwego, ciepła topnienia (krzepnięcia) i parowania (skraplania);
obliczać ilość energii potrzebnej do ogrzania ciała o zadany przyrost temperatury;
obliczać ilość energii potrzebnej do stopienia lub odparowania zadanej ilości substancji.
Ile energii (ciepła) potrzeba do ogrzania szklanki wody? Od czego to zależy? Czy tyle samo wystarczy do ogrzania szklanki oleju?
Zbadanie, od czego zależy ilość energii potrzebnej do ogrzania substancji.
kuchenka elektryczna lub inne źródło ciepła o stałej stabilnej mocy – istotne jest, aby w jednakowych odstępach czasu źródło to dostarczało podobną ilość energii (ciepła);
termometr o zakresie od 0 do 50℃;
waga;
stoper;
dwa jednakowe, metalowe naczynia o pojemności około 750 ml (najlepiej zewnętrzne naczynia od kalorymetru szkolnego z pokrywą wyposażoną w otwór na termometr i mieszadełko);
mieszadełko do mieszania cieczy;
statyw z uchwytem do termometru – jeśli używasz naczynia bez pokrywy,
woda;
olej jadalny;
rękawice ochronne – mogą być kuchenne;
papierowe ręczniki lub ściereczki.
Jedno z naczyń ustaw na wadze i ją wytarujwytaruj.
Wlej do tego naczynia 250 g zimnej wody.
Przykryj naczynie, a w pokrywie umieść termometr i mieszadełko.
RQPz2w0CXA7oh1  Źródło: Tomorrow Sp.z o.o., licencja: CC BY 3.0.
Źródło: Tomorrow Sp.z o.o., licencja: CC BY 3.0.Zmierz temperaturę początkową wody, czyli zanurz termometr w wodzie, odczekaj 2–3 minuty, zamieszaj wodę i odczytaj wskazanie termometru.
Ustaw naczynie na rozgrzanej płycie kuchenki i włącz stoper.
Jeśli używasz naczynia bez pokrywy, to w wodzie zanurz termometr zamocowany na statywie. Sposób ustawienia termometru przedstawiono na rysunku.
RlHFYCjom2VuZ1 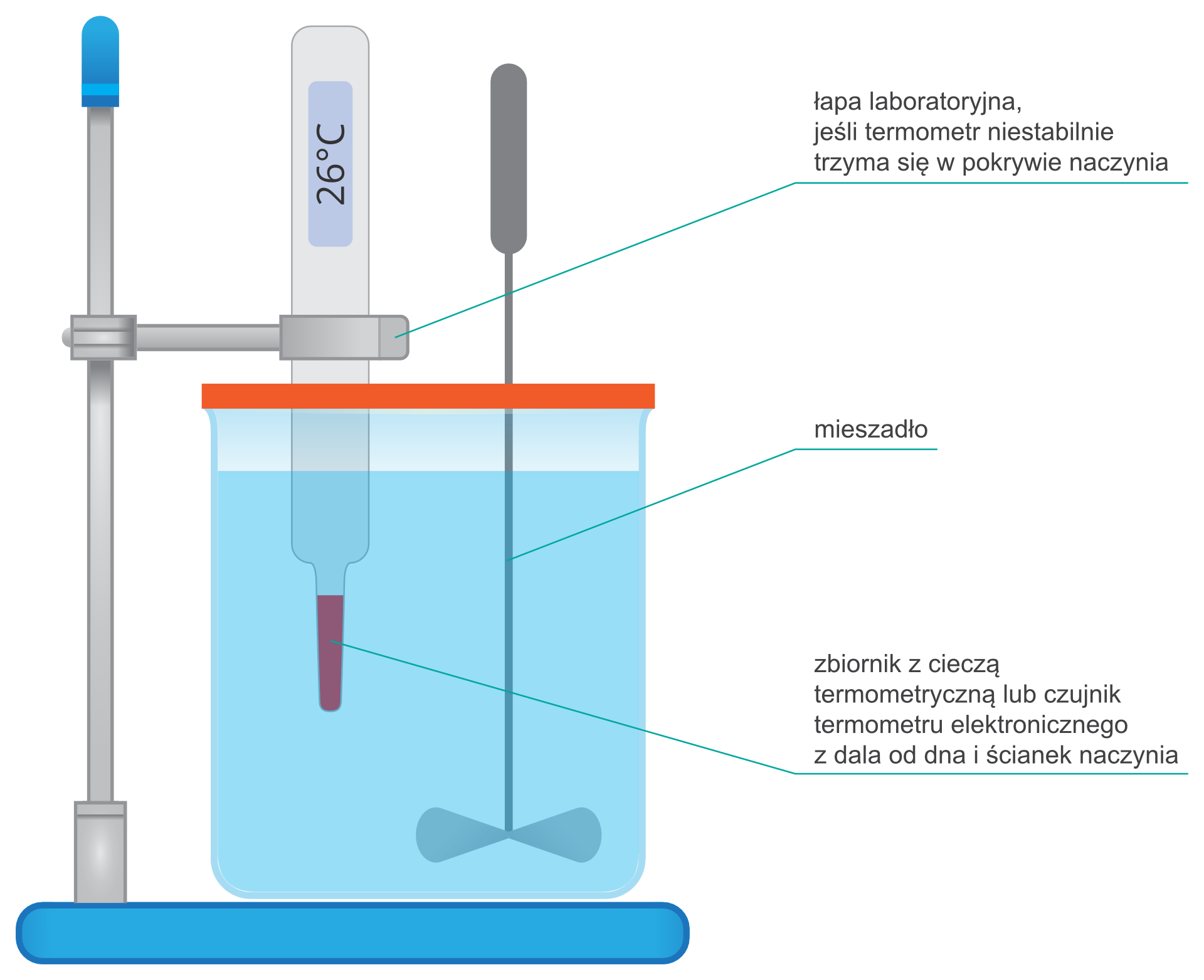 Źródło: Dariusz Adryan, licencja: CC BY 3.0.
Źródło: Dariusz Adryan, licencja: CC BY 3.0.Obserwuj termometr i zanotuj czas, po którym temperatura wody wzrośnie o 10℃ (w stosunku do temperatury początkowej) – nie wyłączaj stopera!
Nadal obserwuj wskazania termometru i zanotuj czas, po którym temperatura wrośnie o kolejne 10℃ (w sumie o 20℃ od temperatury początkowej). Wyłącz stoper.
Załóż rękawice i ostrożnie zdejmij naczynie z kuchenki, wylej gorącą wodę z naczynia, osusz je i pozostaw do ostygnięcia.
Drugie naczynie postaw na wadze i wytaruj ją.
Do tego naczynia wlej 500 g wody i powtórz czynności od 4 do 8.
Do ostudzonego pierwszego naczynia wlej 500 g oleju.
Zmierz temperaturę początkową oleju, a naczynie ustaw na kuchence.
W przypadku oleju powtórz czynności opisane w punktach od 5 do 7.
Wyłącz kuchenkę i gorące przedmioty (naczynie z olejem, kuchenkę) pozostaw do ostygnięcia w bezpiecznym miejscu.
Wyniki pomiarów na bieżąco notuj w tabeli.
Wyniki pomiarów Woda
=………min
=………min
=………min
=………min
Olej
=………min
=………min
Z przeprowadzonych obserwacji wynika, że czas ogrzewania cieczy (tym samym ilość dostarczonej energii) zależy od tego, jaki przyrost temperatury chcemy uzyskać, a także od od masy i od rodzaju ogrzewanej cieczy:
aby zwiększyć temperaturę dwa razy większej masy wody o tyle samo stopni Celsjusza, należy dostarczyć dwukrotnie większą ilość energii cieplnej (ciepła);
dwa razy większy przyrost temperatury tej samej masy wody wymaga dwukrotnie większej ilości ciepła;
podniesienie temperatury o tyle samo stopni takiej samej masy oleju co wody wymaga dostarczenia mniejszej ilości ciepła w przypadku oleju.
Aby móc porównywać własności cieplne różnych substancji, wprowadzono pojęcie ciepła właściwego.
– ilość energii cieplnej potrzebna do ogrzania 1 kilograma substancji o jeden stopień Celsjusza (jeden kelwin). Jest to wielkość charakteryzująca daną substancję. Jednostką ciepła właściwego w układzie SI jest .
Definicję tę możemy zapisać za pomocą wzoru:
gdzie:
– ciepło właściwe;
– masa ciała;
– przyrost temperatury;
– energia (ciepło) dostarczona do ciała.
Wartości ciepła właściwego kilku wybranych substancji przedstawia poniższa tabela.
Ciała stałe | Ciepło właściwe | Ciecze | Ciepło właściwe | Gazy | Ciepło właściwe |
ołów | 130 | rtęć | 140 | metan | 1 854 |
szkło | 700 | nafta | 2 210 | dwutlenek węgla | 654 |
miedź | 380 | benzyna | 2 090 | powietrze | 729 |
złoto | 130 | gliceryna | 2 430 | hel | 3 140 |
lód | 2 090 | woda | 4 180 | para wodna | 1 380 |
beton | 920 | eter | 2 340 | tlen | 649 |
Podane w tabeli wartości ciepła właściwego gazów odnoszą się do sytuacji, w której ogrzewany gaz zachowuje stałą objętość. O tym, dlaczego wartości tego ciepła są inne przy odmiennych sposobach ogrzewania gazów, dowiesz się, gdy wybierzesz w liceum rozszerzony program fizyki.
Ciepło właściwe danej substancji zależy od
- rodzaju substancji i stanu jej skupienia.
- ilości energii wewnętrznej zawartej w ciele wykonanym z tej substancji.
- masy i przyrostu temperatury tej substancji.
- tylko od rodzaju substancji z jakiej wykonane jest ciało.
Jeśli znamy wartość ciepła właściwego dla danej substancji, możemy obliczyć przyrost temperatury ciała o znanej masie po dostarczeniu mu jakiejś porcji ciepła.
O ile wzrośnie temperatura betonowej kostki o masie , jeśli dostarczymy jej energii (ciepła)?
Analiza zadania:
Korzystamy ze wzoru na ciepło właściwe:
,
który po przekształceniu ma postać:
,
.
Dane:
,
,
.
Szukane:
Obliczenia:
Po podstawieniu danych otrzymujemy:
.
Odpowiedź:
Temperatura kostki wzrośnie o 2 kelwiny, czyli o 2 stopnie Celsjusza (przyrost temperatury jest taki sam w skalach Kelvina i Celsjusza).
Jeśli znamy wartość ciepła właściwego, możemy też obliczyć ilość energii potrzebnej do uzyskania wyższej temperatury ciała.
Ile ciepła trzeba dostarczyć, aby ogrzać powietrze w pokoju o 10°C? Objętość pokoju wynosi , gęstość powietrza – a ciepło właściwe powietrza ma wartość .
Analiza zadania:
Ilość potrzebnego ciepła możemy obliczyć, korzystając z definicji ciepła właściwego, tak jak w poprzednim przykładzie:
.
Do dalszych obliczeń potrzebna jest znajomość masy ogrzewanego ciała. Masę powietrza zawartego w pokoju obliczamy, korzystając z definicji gęstości materii:
, czyli .
Jak widać, do obliczenia masy potrzebna jest znajomość gęstości ciała i jego objętości, wartości ciepła właściwego powietrza i zmiany temperatury.
Dane:
,
,
,
.
Szukane:
Q = ?
Obliczenia:
po podstawieniu masy do wzoru na ciepło właściwe:
.
Odpowiedź:
Aby ogrzać powietrze w tym pokoju o 10 stopni, trzeba dostarczyć 475,85 kilodżuli energii.
Dostarczanie ciepła powoduje wzrost temperatury ciała, co jest równoznaczne ze wzrostem jego energii wewnętrznej. Ale czy zawsze dostarczanie ciepła powoduje wzrost temperatury?
Wykonaj kolejne doświadczenie.
Sprawdzenie, czy dostarczanie ciepła zawsze powoduje wzrost temperatury.
termometr zawierający zakres od do ;
zlewka o pojemności 1000 ml;
mieszadełko do mieszania cieczy;
statyw z uchwytem do termometru;
pokruszony lód – około 1000 gramów (tak zwana kasza lodowa).
Pokruszony lód wsyp do naczynia. Jeśli nie masz takiego lodu, możesz młotkiem pokruszyć większe kawałki lodu lub poprosić o „kaszę lodową” w sklepie rybnym.
Umieść termometr w mieszaninie wody z lodem – zadbaj, aby koniec termometru nie dotykał dna ani ścianek bocznych, lecz był umieszczony w środku mieszaniny.
Przez 15 minut co dwie minuty obserwuj wskazania termometru – przed odczytaniem temperatury zamieszaj mieszaninę wody z lodem.
Jeśli w sali jest drugi termometr, to odczytaj temperaturę powietrza panującą w pomieszczeniu.
Jeśli wszystko wykonałeś poprawnie, to zauważyłeś, że lód stopniowo się topił i powstawała mieszanina wody z lodem z rosnącą zawartością wody.
Temperatura mieszaniny pozostawała niezmieniona i wynosiła 0˚C.
Temperatura otoczenia wynosiła co najmniej 20˚C, co oznacza, że następował przepływ ciepła z otoczenia do lodu (mieszaniny wody i lodu).
Wnioski
Dostarczanie ciepła (energii) do mieszaniny wody z lodem nie powodowało wzrostu jej temperatury.
Do stopienia ciała stałego niezbędna jest energia cieplna.
Należy się spodziewać, że ilość energii potrzebnej do stopienia jakiegoś ciała zależy od jego masy i od rodzaju substancji, z której wykonano to ciało.
Odpowiedz na pytanie postawione we wstępie do tej lekcji: dlaczego lód na powierzchni jeziora nie topi się od razu, gdy temperatura wzrasta powyżej zera?
Aby zaszedł proces odwrotny do topnienia – czyli zamiana cieczy w ciało stałe (krzepnięcie), również niezbędna jest wymiana energii. Jednak w tym procesie ciało musi oddać ciepło (energię) do otoczenia, zmniejszając swoją energię wewnętrzną.
W celu porównywania właściwości różnych materiałów wprowadza się pojęcie ciepła topnienia lub ciepło krzepnięcia. Dla danej substancji jest to ta sama wartość.
– ilość ciepła (energii), jaką należy dostarczyć (odebrać), aby stopić (zestalić) 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła topnienia w układzie SI jest . Definicję tę możemy zapisać za pomocą wzoru:
gdzie:
– ciepło topnienia;
– masa ciała;
– energia (ciepło) dostarczone do ciała.
Powyższe zależności są prawdziwe, jeżeli temperatura w czasie procesu topnienia lub krzepnięcia jest stała – czyli tak, jak w przypadku ciał o budowie krystalicznej.
Wartości ciepła topnienia kilku wybranych substancji przedstawia poniższa tabela.
Ciała stałe | Ciepło topnienia |
ołów | 25 000 |
cynk | 118 000 |
złoto | 63 000 |
żelazo | 270 000 |
lód | 335 000 |
Ile energii trzeba zużyć, aby stopić bryłkę ołowiu o masie (w stałej temperaturze topnienia)?
Analiza zadania:
Korzystamy ze wzoru definiującego ciepło topnienia: .
Po jego przekształceniu otrzymujemy: .
Jak widać, do obliczenia potrzebnej ilości ciepła potrzebne są wartości ciepła topnienia i masy ciała.
Dane:
(z tabeli nr 3),
.
Szukane:
Obliczenia:
.
Odpowiedź:
Do stopienia 100 gramów ołowiu (w stałej temperaturze topnienia) potrzeba 2,5 kilodżula energii.
Wykonajmy kolejne doświadczenie.
Zbadanie, czy każde dostarczanie energii powoduje wzrost temperatury ciała.
kuchenka elektryczna lub inne źródło ciepła o stałej stabilnej mocy – istotne jest, aby w jednakowych odstępach czasu źródło to dostarczało jednakowych ilości energii (ciepła);
termometr o zakresie od do ;
metalowe naczynie o pojemności około (najlepiej zewnętrzne naczynia od kalorymetru szkolnego z pokrywą wyposażoną w otwór na termometr i mieszadełko);
statyw z uchwytem do termometru – jeśli używasz naczynia bez pokrywy;
woda;
rękawice ochronne – mogą być kuchenne;
papierowe ręczniki lub ściereczki.
Do naczynia wlej około wody i postaw je na kuchence.
W wodzie zanurz termometr (sposób mocowania termometru jest taki sam jak w pierwszym doświadczeniu).
Odczekaj kilka minut, aż woda zacznie wrzeć.
Odczytuj wskazania termometru przez kilka minut od rozpoczęcia wrzenia.
Wyłącz kuchenkę i poczekaj, aż wszystko ostygnie.
Podczas gdy woda wrze, jej temperatura pozostaje stała (ok. 100˚C).
Kuchenka była cały czas włączona, co oznacza, że energia (ciepło) była cały czas dostarczana do wody.
Wnioski:
Dostarczanie ciepła (energii) do wrzącej wody nie powodowało wzrostu jej temperatury, tylko wrzenie – czyli parowanie cieczy w całej objętości.
Wrzenie (parowanie w całej objętości cieczy) wymaga dostarczania energii.
Należy się spodziewać, że ilość energii potrzebnej do odparowania jakiejś cieczy
zależy od ilości tej cieczy i rodzaju cieczy (substancji).
Aby zaszedł proces odwrotny, czyli zamiana gazu w ciecz (skraplanie), również niezbędna jest wymiana energii. Jednak w tym procesie gaz musi oddać ciepło (energię) do otoczenia, zmniejszając swoją energię wewnętrzną.
W celu porównywania właściwości różnych materiałów wprowadza się pojęcia ciepło parowania i ciepło skraplania. Dla danej substancji jest to taka sama wielkość.
– ilość energii cieplnej (ciepła), jaką należy dostarczyć (odebrać), aby odparować (skroplić) 1 kilogram danej substancji w danej temperaturze. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła parowania w układzie SI jest .
Definicję tę możemy zapisać za pomocą wzoru:
gdzie:
– ciepło parowania;
– masa ciała;
– ilość ciepła dostarczona ciału.
Ciepło parowania dla danej substancji zależy od ciśnienia i temperatury. Im wyższa temperatura, tym ciepło parowania jest mniejsze.
Wartości ciepła parowania kilku wybranych substancji przedstawia poniższa tabela.
Ciecz | Ciepło parowania |
rtęć | 290 000 |
eter | 355 000 |
kwas octowy | 395 000 |
etanol | 963 000 |
woda | 2 260 000 |
Jaką ilość eteru można odparować kosztem ciepła wydzielonego podczas skraplania pary wodnej?
Analiza zadania:
Korzystając z definicji ciepła parowania, obliczamy ilość energii wydzielonej podczas skraplania pary wodnej:
.
Czyli:
.
Dane:
,
.
Obliczenia:
.
Przeprowadźmy obliczenia ilości eteru odparowanego ciepłem :
,
,
.
Dane:
,
(zgodnie z wynikiem poprzednich obliczeń).
Obliczenia:
.
Odpowiedź:
Kosztem energii powstałej ze skroplenia pary wodnej można odparować około 6,37 kg eteru.
Czy więcej energii potrzeba do stopienia lodu, czy do odparowania takiej samej ilości wody? Odpowiedź uzasadnij, powołując się na wartości odpowiednich wielkości fizycznych.
Które z poniższych twierdzeń jest prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Podczas powstawania rosy (skraplanie) woda oddaje ciepło do otoczenia. | □ | □ |
| Kostki lodu topniejące w szklance z napojem oddają energię do napoju. | □ | □ |
| Woda zamarzająca na powierzchni jeziora pobiera energię z otoczenia. | □ | □ |
| Woda parująca na powierzchni skóry człowieka pobiera ciepło ze skóry. | □ | □ |
| Aby stopił się śnieg wniesiony do mieszkania, musi pobrać ciepło z otoczenia. | □ | □ |
| Aby stopił się śnieg wniesiony do mieszkania, musi oddać zimno do otoczenia. | □ | □ |
Podsumowanie
Ilość energii potrzebnej do ogrzania ciała zależy od tego, jaki przyrost temperatury chcemy uzyskać, a także od masy ogrzewanego ciała oraz od rodzaju substancji.
Do porównywania cieplnych właściwości ciał służy ciepło właściwe.
Ciepło właściwe to ilość energii cieplnej (ciepła) potrzebna do ogrzania 1 kilograma substancji o jeden stopień Celsjusza (jeden kelwin). Jest to wielkość charakteryzująca daną substancję.
Jednostką ciepła właściwego w układzie SI jest .
Definicję ciepła właściwego możemy zapisać za pomocą wzoru: ,
gdzie: – ciepło właściwe, – masa ciała, – przyrost temperatury, – energia (ciepło) dostarczone do ciała.Aby stopić ciało stałe, należy dostarczyć energię, aby zaś zestalić ciecz, trzeba pobrać od niej energię.
Ciepło topnienia to ilość energii, jaką należy dostarczyć, aby stopić 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła topnienia w układzie SI jest .
Ciepło krzepnięcia to ilość energii, jaką należy odebrać, aby zestalić 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła krzepnięcia w układzie SI jest .
Definicję ciepła topnienia możemy zapisać za pomocą wzoru: ,
gdzie: – ciepło topnienia, – masa ciała, – energia (ciepło) dostarczone do ciała.Parowanie cieczy oraz wrzenie (parowanie w całej objętości cieczy) wymagają dostarczania energii cieplnej do cieczy, natomiast skraplanie wymaga odprowadzania tej energii od substancji w fazie gazowej.
Ciepło parowania to ilość energii (ciepła), jaką należy dostarczyć, aby odparować 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła parowania w układzie SI jest .
Ciepło skraplania to ilość energii (ciepła), jaką należy odebrać, aby skroplić 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła parowania w układzie SI jest .
Definicję ciepła parowania możemy zapisać za pomocą wzoru: ,
gdzie: – ciepło topnienia, – masa ciała, – energia (ciepło) dostarczone do ciała.
Ile energii trzeba zużyć, aby parafiny ogrzać do temperatury topnienia, a następnie stopić? Temperatura początkowa parafiny wynosi . Brakujące dane znajdź w tablicach lub w Internecie.
O ile zmieni się energia wewnętrzna gorącej herbaty podczas stygnięcia od do ?
Oblicz ciepło potrzebne do stopienia lodu pokrywającego staw o powierzchni , jeśli grubość pokrywy lodowej wynosi . Gęstość lodu ma wartość . Ciepło topnienia lodu znajdź w tabeli. Przyjmij, że temperatura lodu wynosi 0°C.
*Oblicz moc, jaką musiałoby mieć źródło ciepła, żeby ten lód stopił się w ciągu 1 dnia (24 godzin).
Słowniczek
– kilka czynności (obciążanie szalek, regulacja) dokonywanych przed ważeniem, których zadaniem jest doprowadzenie wagi do stanu równowagi lub też wyznaczenie rzeczywistej masy towaru bez opakowania (tary).