Podsumowanie wiadomości z działu I
W tym dziale zapoznaliśmy was z obiektami widocznymi na wieczornym niebie. Opisaliśmy zjawiska, które można na nim zaobserwować, oraz podaliśmy wyjaśnienia niektórych z nich. Przedstawiliśmy prawa powszechnego ciążenia i wpływ sił grawitacyjnych na ruch różnych obiektów w pobliżu Ziemi oraz dużo dalej – w Układzie Słonecznym, Galaktyce, Kosmosie. Ponieważ ruch planet, księżyców i sztucznych satelitów jest ruchem krzywoliniowym, a w przybliżeniu także ruchem po okręgu, nauczyliśmy was opisu takiego ruchu oraz opisaliśmy siłę dośrodkową jako jego przyczynę.

1. Obiekty i zjawiska widoczne na niebie
Gwiazdy, planety, Księżyc i poruszające się sztuczne satelity możemy zauważyć nawet podczas krótkiej obserwacji nocnego, bezchmurego nieba.
Ruch sfery niebieskiej (ze wschodu na zachód) i ruch Księżyca (z zachodu na wschód) w stosunku do gwiazd zauważymy po kilku godzinach obserwacji.
Cykl faz Księżyca wymaga kilku tygodni obserwacji.
Przesuwanie się planet na tle gwiazd widoczne jest po kilku lub kilkunastu miesiącach obserwacji.
Gwiazdy widoczne na niebie mają różną jasność – astronomowie mówią, że mają one różną wielkość gwiazdową. Przykładowo: gwiazda drugiej wielkości gwiazdowej świeci na niebie jaśniej niż gwiazda czwartej wielkości gwiazdowej.
Do przeprowadzenia obserwacji nieba przydatne są obrotowe mapy nieba lub program Stellarium.

2. Księżyc – nasz naturalny satelita
Księżyc jest naturalnym satelitą Ziemi; pełen obieg Księżyca wokół Ziemi trwa około 27,3 doby. Jego tor ruchu jest elipsą, a średnia odległość od Księżyca do Ziemi wynosi ok. 380 tys. km.
Obserwowany kształt tarczy Księżyca zależy od wzajemnego położenia Słońca, Ziemi i Księżyca. Fazy Księżyca są skutkiem jego ruchu obiegowego wokół Ziemi i zmiany oświetlenia jego powierzchni, która jest widoczna z Ziemi, przez Słońce.
Zaćmienie Księżyca zachodzi, gdy znajdzie się on w cieniu Ziemiw cieniu Ziemi.
Powierzchnia Księżyca pokryta jest zwietrzałymi skałami, tzw. regolitem.
Informacje nt. budowy Księżyca uzyskano dzięki różnym projektom badawczym, m.in dzięki lądowaniu człowieka na jego powierzchni.

3. Ruch planet
Planety poruszają się na niebie w skomlikowany sposób – zmieniają swoją prędkość i kierunek ruchu, zakreślają pętle na tle gwiazdpętle na tle gwiazd.
Według systemu geocentrycznego skomplikowane drogi planet są wynikiem ruchu planety odbywającego się po kilku okręgach jednocześnie.
Zgodnie z systemem heliocentrycznym Ziemia porusza się dookoła Słońca; pozorny ruch planet na niebie (wynikający z ruchu Ziemi) nakłada się na ich rzeczywisty ruch względem gwiazd.

4. Pomiar odległości w astronomii
Do wyznaczenia odległości do bliskich obiektów, takich jak Księżyc czy planety, wystarczą dwa punkty na Ziemi. Zmiana położenia obserwatora o kilka czy kilkanaście tysięcy kilometrów wystarczy, aby wykorzystać zjawiskoparalaksy geocentrycznejparalaksy geocentryczneji wyznaczyć szukane odległości.
Obecnie odległość od Ziemi do Księżyca wyznacza się za pomocą zjawiska odbicia światła laserowego wysłanego z Ziemi i odbitego od specjalnych odbłyśników umieszczonych na powierzchni naszego naturalnego satelity, m.in. dzięki wyprawom kosmicznym.
Zjawiskoparalaksy heliocentrycznejparalaksy heliocentrycznej (pozornego przesuwania się gwiazd znajdujących się bliżej Ziemi w stosunku do tych dalszych, co jest wynikiem zmiany położenia obserwatora) pozwoliło potwierdzić teorię Kopernika i na wyznaczyć odległości do najbliższych gwiazd.
Jednostki odległości używane w astronomii:
jednostka astronomiczna (1 AU) – jest równa średniej odległości między Ziemią a Słońcem, czyli 149 mln km; jest najwygodniejszą jednostką w Układzie Słonecznym;
parsek (1 pc) (skrót pochodzi od wyrażenia paralaksa sekundowa) – dla gwiazdy odległej o 1 parsek kąt paralaksy heliocentrycznej wynosi jedną sekundę kątową. Jednostki tej używają głównie astronomowie, aby wyrazić odległość do gwiazd i innych odległych obiektów astronomicznych;
rok świetlny (1 ly) – odległość, jaką światło przebywa w próżni w ciągu jednego roku. Jeżeli wyrażamy odległości w latach świetlnych, wiemy jednocześnie, ile lat wcześniej zdarzyło się to, co obecnie obserwujemy.
5. Ruch po okręgu
Do opisu ruchu po okręgu posługujemy się pojęciami „okresu obiegu” i „częstotliwość”.
Okresem () nazywamy czas potrzebny na wykonanie jednego pełnego obiegu po okręgu.
Częstotliwością () nazywamy liczbę pełnych obiegów wykonywanych w czasie 1 sekundy.
2. W ruchu jednostajnym po okręgu wartość prędkości liniowej jest stała, lecz zmieniają się jej kierunek i zwrot.
3. Prędkość liniowa jest styczna do okręgu.
4. Prędkość liniową () obliczamy ze wzoru:
lub , gdzie: 2πr – droga przebyta w ciągu jednego okresu .

6. Siła dośrodkowa
Siłą odpowiedzialną za ruch ciała po okręgu jest siła dośrodkowa.
Wartość siły dośrodkowej obliczamy według wzoru:
gdzie:
– masa poruszającego się ciała;
– prędkość ciała;
– promień okręgu zakreślanego przez poruszające się ciało.Funkcję siły dośrodkowej może pełnić pojedyncza siła działająca na ciało (np. siła grawitacyjna, magnetyczna, sprężystości) lub wypadkowa kilku różnych sił działających na ciało.

7. Prawo powszechnego ciążenia
Każde dwa ciała przyciągają się wzajemnie siłami grawitacji.
Wartość siły grawitacji zależy od masy ciał i odległości między ich środkami; siła ta jest:
wprost proporcjonalna do iloczynu mas;
odwrotnie proporcjonalna do kwadratu odległości między ciałami.
Wartość siły grawitacji dla ciał kulistych lub takich, które możemy traktować jako punktowe (z uwagi na bardzo dużą, w porównaniu z rozmiarami samych ciał, odległość między nimi), można obliczyć ze wzoru:
gdzie:
– stała grawitacji;
, – masy ciał;
– odległość między środkami ciał.Siła grawitacji pełni funkcję siły dośrodkowej w ruchu planet wokół Słońca czy ruchu księżyców wokół planet bądź sztucznych satelitów poruszających się wokół Ziemi.

8. Prędkości kosmiczne
Na planetę krążącą wokół Słońca lub innej gwiazdy działa siła grawitacji, która jest siłą dośrodkową.
Prędkość, z jaką planeta, księżyc planety lub sztuczny satelita Ziemi poruza się po orbicie o promieniu wokół ciała centralnego, wyraża się zależnością: .
Masa jest to masa ciała centralnego, wokół którego krąży drugie ciało, które ma znacznie mniejszą masę od ciała centralnego.I prędkość kosmiczna to wartość prędkości, którą należy nadać ciału (stycznie do powierzchni Ziemi), aby mogło ono krążyć po orbicie kołowej o promieniu równym promieniowi Ziemi.
Znajomość okresu obiegu satelity wokół ciała centralnego i jego odległości od środka ciała centralnego pozwala wyznaczyc masę ciała centralnego: Słońca, planety czy nawet planetoidy (wiele z nich ma księżyce mniejsze od siebie).
Obecnie tylko rakieta wielostopniowa osiąga odpowiednie prędkości, które pozwalają umieścić statek kosmiczny na orbicie lub polecieć na Księżyc.

9. Ruch sztucznych satelitów Ziemi
Satelity, czyli ciała krążące wokół Ziemi, innych planet lub Słońca, mają różnorodne zastosowanie – od naukowego po komercyjne (telekomunikacja, audycje radiowe i telewizyjne). Niektóre satelity są przeznaczone do celów wojskowych lub wywiadowczych.
Dzięki satelitom możemy ogladać zjawiska niewidoczne z powierzchni Ziemi albo zbierać doświadczenia związane z długim pobytem człowieka w stanie nieważkości.

10. Przeciążenie i nieważkość
Gdy rakieta porusza się pionowo w górę z określonym przyspieszeniem (podczas startu), to doznaje przeciążenia. Oznacza to zwiększony nacisk na fotele, na których leżą kosmonauci podczas startu. Siła, z jaką oni naciskają na fotele, jest kilkakrotnie większa od ciężaru kosmonautów;
gdzie:siła nacisku;
– siła grawitacji;
– przyspieszenie, z jakim porusza się rakieta podczas startu.Ciało poruszające się pionowo w dół z pewnym przyspieszeniem (np. w windzie) różnym od przyspieszenia grawitacyjnego znajduje się w stanie niedociążenia. Ciężar pozorny takiego ciała jest mniejszy od ciężaru mierzonego w stanie spoczynku. Wartość siły nacisku na podłoże obliczamy ze wzoru: .
Gdy winda, w której znajduje się ciało, spada swobodnie, mamy do czynienia ze stanem nieważkości. Oznacza to brak wzajemnego nacisku ciała i windy.
W pojeździe kosmicznym poruszającym się tylko pod wpływem siły grawitacji (bez włączonych silników) panuje stan nieważkości. Wynika on z tego, że zarówno pojazd, jak i jego załoga doznają jednakowych przyspieszeń i dlatego te ciała na siebie nie naciskają.

11. Satelita geostacjonarny
Satelita geostacjonarny to satelita, który „wisi” stale nad jednym punktem znajdującym się na powierzchni Ziemi (dokładniej: nad punktem na równiku). Krąży dookoła Ziemi, wykonując jeden obieg w czasie 24 godzin (dokładnie: 23 godzin, 56 minut i 4 sekund – bo tyle trwa jeden obrót Ziemi dookoła własnej osi),
Promień orbity takiego satelity wynosi około 42 tys. km, a jego prędkość ma wartość . Satelity tego typu sa wazne, bo większość z nich to satelity telekomunikacyjne, czyli takie, z których są nadawane programy telewizyjne bądź transmitowane rozmowy telefoniczne.

12. Prawa Keplera
Trzy prawa Keplera opisują ruch planet i innych ciał niebieskich dookoła Słońca:
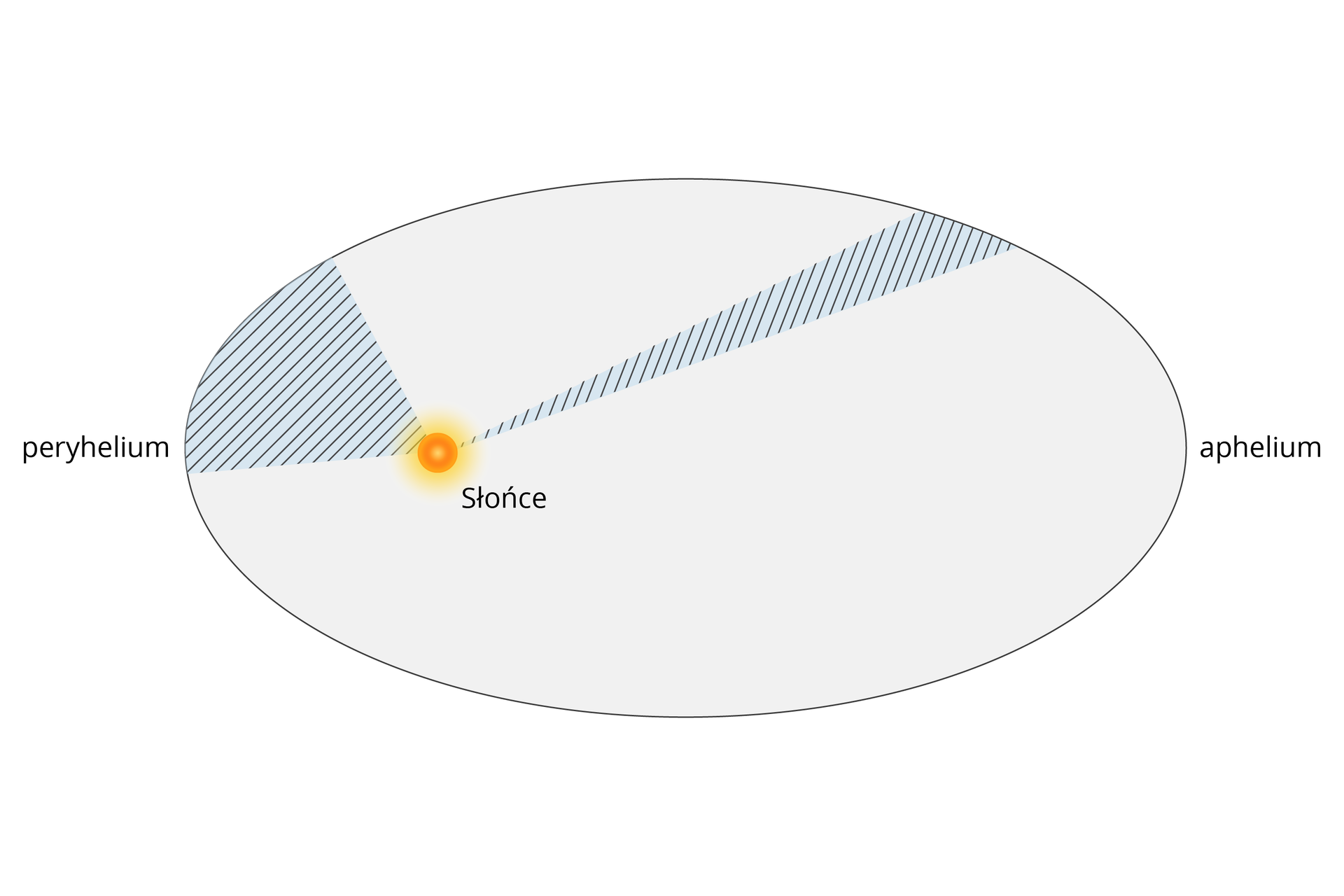
I prawo głosi, że orbity planet są eliptyczne; oznacza to, że odległość od planety do Słońca jest zmienna; punkt leżący najbliżej Słońca nazywamy peryhelium, a najdalej – aphelium;
II prawo mówi o zmiennej prędkości liniowej i kątowej oraz o stałej prędkości polowej planet; prędkość linowa jest największa w peryhelium, a najmniejsza – w aphelium;
III prawo to związek rozmiarów orbit planet i okresów ich obiegu wokół Słońca; tę zależność można zapisać w postaci wzoru:
, gdzie:
Indeks dolny ,,– średnia odległość od planety do Słońca; T1, T2 – okres obiegu dla jednej planety (na przykład Ziemi). Ten wzór można stosować dla dowolnej pary księżyców krążących wokół jednej planety.
15. Układ Słoneczny
Układ Słoneczny to Słońce i osiem planet krążących wokół niego. Są to: Merkury, Wenus, Ziemia, Mars, Jowisz, Saturn, Uran i Neptun.
Oprócz tych planet do Układu należą:
ich księżyce;
różnej wielkości planetoidy oraz tzw. planety karłowate (m.in. Pluton, Eris, Ceres);
komety, krążące wokół Słońca po bardzo wydłużonych orbitach eliptycznych.

16. Budowa Galaktyki
Słońce i inne ciała krążące wokół niego są częścią Galaktyki widocznej na niebie jako Droga Mleczna. Nasza Galaktyka liczy od 200 do 300 miliardów gwiazd. Droga Mleczna to jedna z większych galaktyk we Wszechświecie – ma średnicę równą ok. 120 tys. lat świetlnych. Kształtem przypomina spiralę z poprzeczką.
Nasz Układ Słoneczny znajduje się nieco bliżej niż 30 000 lat świetlnych od centrum Galaktyki i leży prawie w płaszczyźnie równika, w tzw. ramieniu Oriona. Słońce i planety Układu Słonecznego obiegają centrum Galaktyki. Prędkość Słońca na tej orbicie wynosi ok. 270 km/s, co daje okres obiegu wokół centrum Galaktyki wynoszący ponad 200 mln lat.
W Galaktyce znajdują się bardzo różne gwiazdy. Najwięcej jest gwiazd podobnych do Słońca – mają one średnicę do kilkunastu razy większą niż średnica Słońca. Znacznie mniej jest gwiazd większych, mających średnicę ok. 100 razy większą niż średnica Słońca (olbrzymy), i mające średnicę około 1000 razy większą niz średnica Słońca (nadolbrzymy). Najmniejsze gwiazdy to białe karły, które mają wyższą temperaturę niż temperatura naszego Słońca, ich średnica jest mniej więcej taka sama jak średnica Ziemi. Odkryto także tzw. pulsary – mają one średnicę 10–20 km i prawdopodobnie są gwiazdami neutronowymi.

Test
Najodleglejsza planeta Układu Słonecznego - Neptun - obiega Słońce w ciągu 165 lat. Jaka jest średnia odległość planety od Słońca wyrażona w jednostkach astronomicznych?
- 30 j. a.
- 13 j. a.
- 2120 j. a.
- 165 j. a.
- Nie można obliczyć tej odległości – w treści zadania podano za mało danych.
- 5,5 j. a.
- 40 j. a.
Płyta CD wykonuje od 200 do 500 obrotów na minutę. W jakim zakresie zmienia się okres obrotów płyty? Wskaż poprawne odpowiedzi.
- od 0,3 s do 0,12 s
- od 0,005 min do 0,002 min
- od 3,333 s do 8,333 s
- od 0,5 min do 0,2 min
- od 0,05 min do 0,02 min
- od 0,03 s do 0,012 s
- od 0,3333 s do 0,8333 s
W wirówce znajdują się dwie cząsteczki A i B. Masa cząsteczki A jest dwa razy większa od masy cząsteczki B. Na którą cząsteczkę i ile razy większa siła dośrodkowa musi działać, aby obie poruszały się po okręgu o tym samym promieniu i z tą samą prędkością?
- Na cząsteczkę A musi działać dwa razy większa siła.
- Na obie cząsteczki musi działać taka sama siła.
- Na cząsteczkę B musi działać dwa razy większa siła.
- Na cząsteczkę A musi działać cztery razy większa siła.
- Na cząsteczkę B musi działać cztery razy większa siła.
Na samochód pokonujący łagodny zakręt z prędkością o wartości 40 km/h działa siła dośrodkowa o wartości 4 kN.
Oblicz siłę potrzebną, aby ten sam samochód pokonał ten zakręt z prędkością o wartości 80 km/h?
- 16 kN
- 16 000N
- 8 kN
- 8 000 N
- 4 000 N
- 4 kN
- 6 kN
- 6 000 N
Strumień elektronów porusza się po okręgu o promieniu R. W pewnym momencie zaobserwowano, że promień toru ruchu cząstek wzrósł do wartości 1,5 R. Jak zmieniła się wartość siły dośrodkowej działającej na cząstki, jeśli wiadomo, że wartość ich prędkości nie uległa zmianie?
- Siła dośrodkowa zmalała razy.
- Siła dośrodkowa wzrosła razy.
- Siła dośrodkowa nie zmieniła się.
- Siła dośrodkowa zmalała razy.
- Siła dośrodkowa wzrosła razy.
Trzy satelity , , i krążą wokół Ziemi na jednej orbicie, to znaczy, że wszystkie są w tej samej odległości od Ziemi. Masy tych satelitów wynoszą odpowiednio: 10 kg, 100 kg, 200 kg.
Na podstawie tych informacji, oceń prawdziwość poniższych zdań.
| Prawda | Fałsz | |
| Prędkości wszystkich trzech satelitów są takie same. | □ | □ |
| Ziemia najsilniej przyciąga satelitę . | □ | □ |
| Siła grawitacyjna, z jaką Ziemia przyciąga satelitę jest 10 razy mniejsza niż ta działająca na . | □ | □ |
| Siła, z jaką Ziemia przyciąga satelity jest taka sama dla wszystkich trzech obiektów. | □ | □ |
| Satelita porusza się z największą prędkością, a satelita z najmniejszą. | □ | □ |
| Satelity o różnych masach nie mogą krążyć na jednej orbicie. | □ | □ |
Ziemia przyciąga Księżyc siłą F. Odległość Księżyca od Ziemi wynosi D. Jaką wartość miałaby siła, oddziaływania Ziemi na Księżyc, gdyby w wyniku katastrofy kosmicznej Księżyc odsunął się na odległość 2D?
- 1/4 F
- 0,25 F
- 1/2 F
- 0,5 F
- 2 F
- 4 F
- F
Ile czasu potrzebuje satelita geostacjonarny, aby wykonać jedno pełne okrążenie? Wskaż poprawne odpowiedzi.
- Około 24 godzin.
- 1 dobę.
- Tyle ile Ziemia potrzebuje na wykonanie obrotu wokół własnej osi.
- Ten czas zależy od promienia orbity satelity.
- 12 godzin.
- 1 rok.
- Tyle, ile Ziemia potrzebuje na okrążenie Słońca.
Czy wyrzucenie ciała z prędkością o wartości 7,9 km/s (tyle wynosi wartość I prędkości kosmicznej) jest wystarczające, aby stało się ono satelitą Ziemi?
- Nie wystarczy, dodatkowo należy tej prędkości nadać kierunek styczny do powierzchni Ziemi.
- Tak wystarczy, ponieważ jest to wartość I prędkości kosmicznej.
- Tak wystarczy, ale należy wyrzucić ciało pionowo do góry.
Wskaż odpowiedź, w której uporządkowano planety według rosnącej odległości od Słońca.
- Merkury, Mars, Jowisz, Saturn
- Merkury, Jowisz, Saturn, Mars
- Jowisz, Merkury, Mars, Saturn
- Merkury, Saturn, Jowisz, Mars
- Mars, Merkury, Jowisz, Saturn
- Saturn, Merkury, Jowisz, Mars
Siła grawitacji działająca na pojazd kosmiczny znajdujący się na powierzchni Ziemi wynosi 1 000 N. Na jakiej wysokości nad powierzchnią Ziemi siła grawitacji działająca na ten pojazd zmaleje do 250 N?
- Na wysokości równej wartości promienia Ziemi, czyli 6 370 km.
- Na wysokości cztery razy większej od promienia Ziemi.
- Na wysokości trzy razy większej od promienia Ziemi.
- Na wysokości 4 km.
- Na wysokości 2 km.
- Na wysokości równej odległości Ziemi od Księżyca.
Wokół planety Jowisz krąży ponad 60 księżyców. Co stałoby się z tymi księżycami, gdyby nagle zniknęła siła grawitacyjna między Jowiszem a każdym z księżyców?
- Księżyce oddaliłyby się od Jowisza po liniach prostych stycznych do ich dotychczasowych orbit.
- Księżyce nadal krążyłyby po swoich orbitach.
- Księżyce oddalałyby się od Jowisza promieniście.
- Księżyce oddalałyby się od Jowisza po linii spiralnej.
- Księżyce spadłyby na Jowisza.
Zadania
Opisz sposób pomiaru odległości do bliskiej gwiazdy za pomocą paralaksy rocznej (heliocentrycznej). Podaj definicję jednostki odległości używanej przez astronomów i związanej ze zjawiskiem paralaksy.
Widoczny na niebie ruch planet jest skomplikowany; każda planeta zakreśla pętle i zmienia swoją prędkość. Jak ten ruch wyjaśnia teoria geocentryczna, a jak – heliocentryczna? Wyjaśnienia poprzyj odpowiednim rysunkiem.
Wirówka używana w laboratorium analitycznym wykonuje maksymalnie 18 000 obrotów na minutę. Oblicz okres obrotów wirówki, a jej częstotliwość wyraź w hercach.
Na stronie internetowej
http://tvnmeteo.tvn24.pl/informacje‑pogoda/ciekawostki,49/wkrotce‑ksiezyc‑zasloni‑34‑tarczy‑sloncaczekaja‑nas‑utrudnienia,160331,1,0.html
10 marca 2015 można było przeczytać następującą informację:
W piątek 20 marca Polacy powinni spoglądać w niebo. Tego dnia Księżyc przysłoni miejscami nawet 75 proc. tarczy słonecznej. Zjawisko rozpocznie się po godz. 9.40. Jako pierwsi zobaczą je wrocławianie (o godz. 9.41). Następnymi obserwatorami będą mieszkańcy Krakowa i Gdańska. Warszawiacy zobaczą zaćmienie po godz. 9.48.
Największa faza zjawiska (apogeum) rozpocznie się na krótko przed godz. 11.
Naszkicuj wzajemne położenie Słońca, Ziemi i Księżyca w chwili zapowiadanego zjawiska. Nazwij fazę, w jakiej znalazł się Księżyc tego dnia.
W tekstach o gwiazdach i planetach można przeczytać, że „planeta (gwiazda) przechwyciła przelatującą obok planetoidę i ta stała się jej satelitą”. Jak rozumiesz takie sformułowanie? Na czym polega to „przechwycenie”?
* Ziemia krąży wokół Słońca po elipsie zbliżonej kształtem do okręgu; ma prędkośc ok. 30 km/s. Wyobraź sobie, że pewnego letniego dnia zniknęła siła grawitacyjna, jaką Słońce działa na Ziemię. Zastanów się nad następującymi problemami i przygotuj na nie odpowiedź.
Czy w konsekwencji zaniku tej siły ustałyby ruch wirowy Ziemi wokół własnej osi oraz następstwo dni i nocy?
Czy ustałoby następstwo pór roku? Jeśli tak, to czy zawsze byłoby lato?
Czy Ziemia oddalałaby się od Słońca z prędkością większą, mniejszą czy równą 30 km/h? A może nadal krążyłaby wokół Słońca?
Czy ludzie na Ziemi znaleźliby się w stanie nieważkości?
Deimos – jeden z księżyców Marsa – okrąża planetę w ciągu 30 godzin. Odległość między Deimosem a środkiem Marsa wynosi ok. 23 500 km. Udowodnij, że znajomość tych dwóch danych jest wystarczająca, aby obliczyć masę Czerwonej Planety.
Okres obiegu Neptuna, ostatniej planety Układu Słonecznego, trwa około 165 lat. Oblicz średnią odległość Neptuna od Słońca w jednostkach astronomicznych (AU).




