Podstawowe figury geometryczne

Film dostępny na portalu epodreczniki.pl
Animacja

Film dostępny na portalu epodreczniki.pl
Animacja
Gdy patrzymy nocą na rozgwieżdżone niebo, postrzegamy gwiazdy jako punkty.
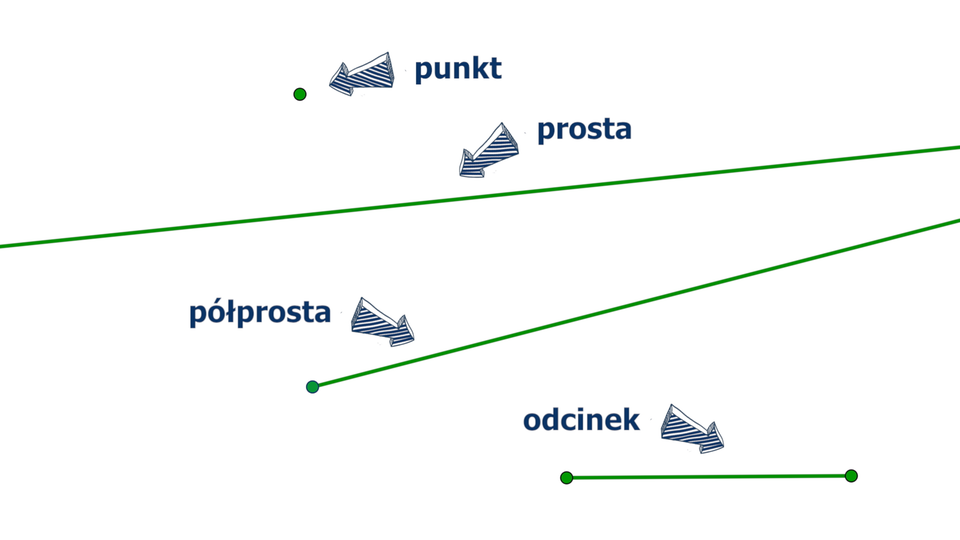
Jednym z podstawowych pojęć w geometrii jest punkt. Zwykle zaznaczamy go kropką i oznaczamy wielką literą.

.
Przygotuj małą kartkę papieru. Zegnij ją dwukrotnie, jak na poniższym rysunku.

Rozłóż kartkę i popatrz, gdzie się przecinają linie zgięcia. Zaznacz kropką punkt przecięcia linii i nazwij go . Wklej kartkę do zeszytu.
Proste, półproste, odcinki
Kolejnym podstawowym pojęciem w geometrii jest prosta.
Prosta nie ma początku ani końca.
Prostą oznaczamy małą literą.
R1VHfFt9cp0uo1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Zaznacz w zeszycie dwa dowolne punkty. Oznacz je literami i Narysuj prostą przechodzącą przez te punkty. Czy możesz narysować więcej takich prostych? Ile prostych przechodzi przez punkty i ? Wybierz odpowiedź.
nieskończenie wiele prostych, trzy proste, jedna prosta, dwie proste
Przez dwa dowolne punkty przechodzi ...........................................................
Na rysunku prosta przechodzi przez punkty i , zatem można ją nazwać prostą lub prostą .

To jest prosta (lub prosta ).
Zaznacz w zeszycie dowolny punkt. Oznacz go literą . Narysuj prostą przechodzącą przez ten punkt. Czy możesz narysować więcej takich prostych? Ile prostych może przechodzić przez jeden dowolny punkt? Wybierz odpowiedź.
dokładnie jedna prosta, dokładnie trzy proste, nieskończenie wiele prostych, dokładnie dwie proste
Przez jeden dowolny punkt może przechodzić ...........................................................
Popatrzmy, jak są położone punkty , , , względem prostej .

Mówimy, że
punkty i należą do prostej lub punkty i leżą na prostej
punkty i nie należą do prostej lub punkty i leżą poza prostą

Spójrz na rysunek i rozstrzygnij, czy zdania są prawdziwe, czy fałszywe.
- Punkt nie należy do prostej .
- Punkt należy do prostej .
- Punkt nie należy do prostej .
- Punkt należy do prostej .
Narysuj prostą . Zaznacz na niej punkt . Punkt podzielił prostą na dwie części. Pokoloruj jedną z nich.
Dowolny punkt leżący na prostej dzieli tę prostą na dwie części. Każdą z tych części nazywamy półprostą. Każda półprosta ma początek, ale nie ma końca. Początkiem półprostej jest punkt dzielący prostą.

Najczęściej półprostą oznaczamy za pomocą dwóch wielkich liter, przy czym pierwsza litera zawsze oznacza początek półprostej.
R2oESQKVXhYDk1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Półprostą można też oznaczyć małą literą.
RIpUQNSYyAIKW1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Zaznacz w zeszycie dwa punkty i . Połącz te punkty linią, rysowaną za pomocą linijki.
Narysowana figura to odcinek.
Każdy odcinek ma dwa końce.
Końce odcinka oznaczamy wielkimi literami. Odcinek możemy też oznaczyć jedną małą literą.
RR88W8auD3rBu1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Film dostępny na portalu epodreczniki.pl
Animacja
Wypisz odcinki, które widzisz na rysunku. Policz, ile jest wszystkich odcinków.

Narysuj otwartą kopertę. Nie odrywaj ołówka od papieru i nie prowadź go dwa razy po tym samym odcinku (oprócz początku i końca odcinka).

Na ile sposobów można narysować otwartą kopertę bez odrywania ołówka od kartki papieru?
Łamana to figura zbudowana z odcinków. Koniec jednego odcinka może być początkiem drugiego odcinka, koniec drugiego odcinka jest początkiem trzeciego, itd.
Odcinki, z których zbudowana jest łamana, to boki łamanej.
Końce odcinków – to wierzchołki łamanej.
RPmKT5KAASjCv1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.To jest łamana zwyczajna otwarta . Ma ona wierzchołków. Boki tej łamanej nie przecinają się.

To jest łamana wiązana. Boki tej łamanej przecinają się.

To jest łamana zwyczajna zamknięta
Która z figur to łamana?
- 7357
- 51397
- 51398
- 51399
- 51400





Narysuj dowolne łamane: zamkniętą i otwartą. Niech każda z nich składa się z odcinków.
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Prosta nie ma początku ani końca.
- Półprosta nie ma początku, ale ma koniec.
- Łamane mogą być otwarte lub zamknięte.
- Odcinek ma początek, ale nie ma końca.
- Punkty oznaczamy małymi literami.
Na rysunku zaznaczono pięć punktów: , , , i .
Narysuj
odcinek
półproste i
proste i
Przyjrzyj się teraz rysunkowi i znajdź na nim wszystkie łamane, których wierzchołkami są nazwane punkty. Ile jest takich łamanych? Podaj ich nazwy i napisz, czy są to łamane otwarte, czy zamknięte.














