Moc prądu elektrycznego
Wiesz już, że taka sama praca może być wykonywana w różnym czasie. Wielkością fizyczną, która opisuje, jak szybko wykonujemy pracę, jest moc.
Jeśli przyjrzysz się uważnie urządzeniom elektrycznym, na ich tabliczkach znamionowych dostrzeżesz zestawy danych opisujące parametry eksploatacyjne. Jednym z nich jest moc. Wiesz już, że moc to szybkość wykonywania pracy, lecz co to tak naprawdę oznacza w przypadku silnika elektrycznego? Czym jest moc prądu elektrycznego?

podać definicję napięcia elektrycznego i jego jednostki – wolta (V);
podać definicję natężenia prądu i jego jednostki – ampera (A);
sformułować prawo Ohma.
opisywać zależność między mocą, napięciem elektrycznym i natężeniem;
rozwiązywać zadania dotyczące mocy prądu.
1. Moc prądu elektrycznego
Na wielu urządzeniach elektrycznych codziennego użytku znajdują się napisy dotyczące ich mocy. Moc () informuje o pracy () wykonywanej przez urządzenie w jednostce czasu ():
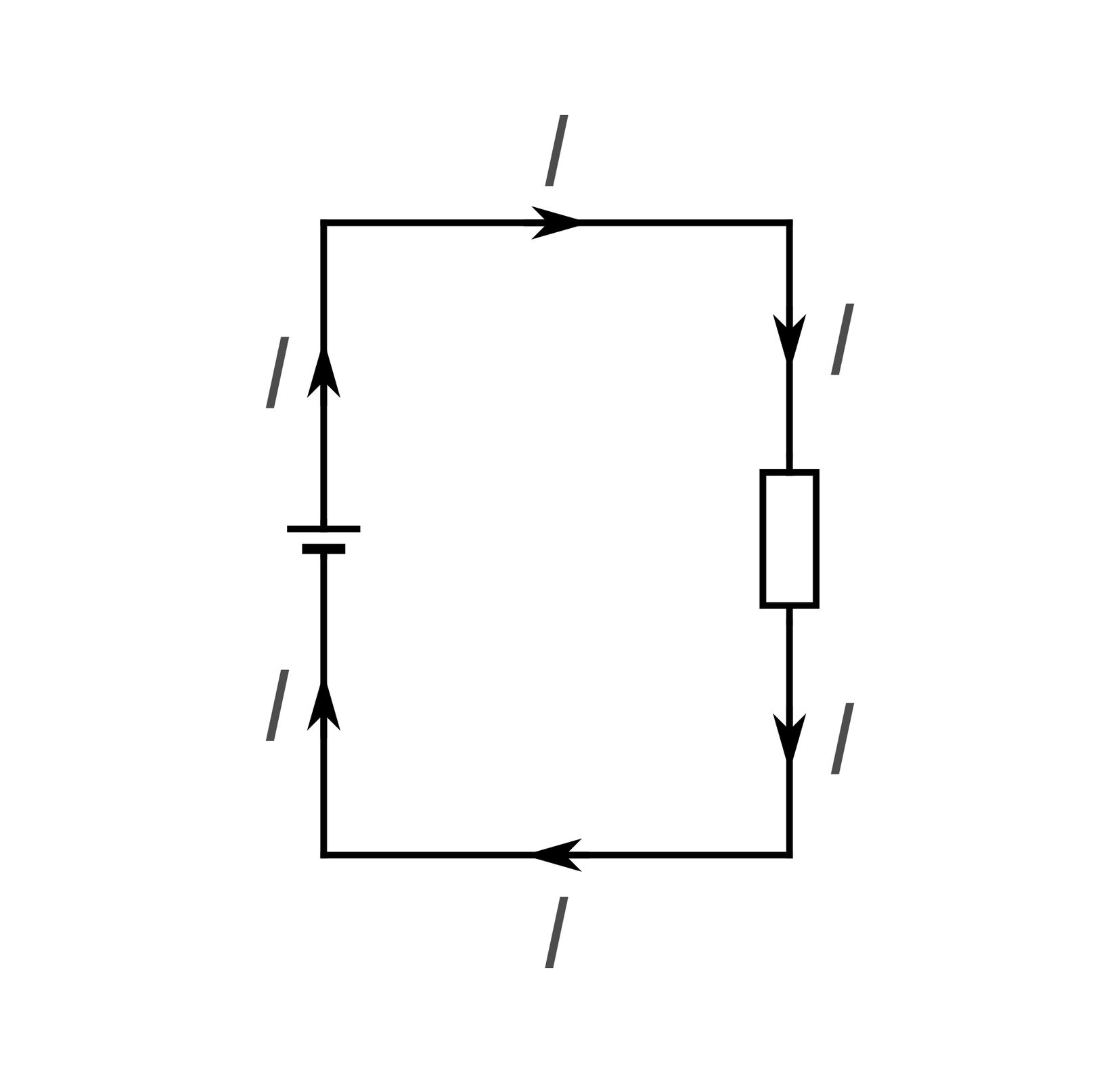
Zastanówmy się, czym jest moc prądu elektrycznego. W tym celu rozważymy obwód elektryczny składający się ze źródła prądu, przewodów i dowolnego elementu, którym może być opornik, akumulator, silnik itp.
Na urządzeniach elektrycznych podane jest także zalecane napięcie elektryczne. W jaki sposób te dwie wielkości są ze sobą związane? Z poprzednich lekcji wiemy, że napięcie (U) między końcami danego odbiornika energii elektrycznej definiowane jest w następujący sposób:
gdzie: W – praca wykonywana przez źródło napięcia w celu przeniesienia ładunku elektrycznego (q) wzdłuż przewodnika.
Wartość ładunku obliczamy za pomocą wzoru (również poznanego podczas pierwszej lekcji w tym dziale):
A zatem: ; , a . Po przekształceniu wzorów otrzymamy:
Z tego zaś wynika (dzieląc obie strony równania przez t), że
– ilość energii przekazywanej ze źródła do opornika; wyznaczamy ją ze wzoru:
gdzie:
– natężenie; – napięcie elektryczne.
Jednostką mocy w układzie SI jest jeden wat (W).
Często używane są wielokrotności tej jednostki: kilowat (kW), czyli 1 000 watów, i megawat (MW), czyli 1 milion watów. Ta ostatnia jednostka stosowana jest najczęściej do opisu mocy wytwarzanej w elektrowniach.
Wyznaczenie mocy żarówki elektrycznej przy napięciu znamionowym (odczytanym na oprawce żarówki).
żarówka (np. z latarki kieszonkowej);
przewody;
miernik uniwersalny;
bateria.
Zbuduj obwód zgodnie z poniższym schematem.
R1RpROKFMWST51  Sposób połączenia elementów doświadczalnego obwodu elektrycznego
Sposób połączenia elementów doświadczalnego obwodu elektrycznegoZmierz wartości napięcia i natężenia prądu elektrycznego w obwodzie.
Oblicz moc żarówki.
Pomiary powtórz trzykrotnie.
Porównaj uzyskany wynik z mocą zapisaną na żarówce. Sporządź notatkę, korzystając z poniższej tabeli.
Nr pomiaru | |||
1 | |||
2 | |||
3 | |||
Wartość średnia | |||
Wyznaczona moc żarówki: ..............
Odczytana nominalna moc żarówki: ..............
Podsumowanie doświadczenia: ..............
Odkurzacz z napisem 2000 W wykona pracę 2000 J w czasie 1 sekundy, a odkurzacz o mocy 2500 W w tym samym czasie wykona pracę równą 2500 J. Jeśli kupisz odkurzacz o mocy 2500 W, będziesz spędzać mniej czasu na odkurzaniu. Ale czy takie rozwiązanie jest tańsze?
Elektryczna energia potencjalna może zamienić się w energię mechaniczną, chemiczną lub ciepło – w zależności od elementu znajdującego się w obwodzie. Jeśli do źródła prądu podłączony zostanie silnik, to nastąpi zamiana w energię mechaniczną. Jeśli tym elementem będzie akumulator (podłączony w celu jego naładowania), to energia zamieni się w energię chemiczną. Jeśli zaś podłączymy opornik, energia zamieni się w energię wewnętrzną (co będzie prowadziło do wzrostu jego temperatury).
Dla odbiornika wydzielającego ciepło, np. opornika lub żarówki, można połączyć wzory na napięcie i moc:
i
W rezultacie otrzymujemy jedną z dwu możliwych zależności:
lub
Powyższe wzory można stosować tylko wtedy, gdy następuje zamiana energii elektrycznej na energię termiczną (wewnętrzną).
Jak działa żarówka?
Jeśli moc rozproszona w przewodzie jest duża, to wytwarzana jest duża ilość ciepła. Ciepło to jest dostarczane do włókna żarowego tak szybko, że nie ma ono czasu na emisję tego ciepła do otoczenia. Następuje gwałtowny wzrost temperatury włókna żarowego. Jeśli temperatura jest wystarczająco wysoka, drut zaczyna się żarzyć i emitować światło. Szacuje się, że ok. 10% energii rozproszonej w żarówce jest zamieniane na światło, a reszta – na ciepło (które przyczynia się do wzrostu temperatury drucika). Spora ilość energii wysyłana jest przez żarówkę do otoczenia.

Prąd o natężeniu 3 A przepływa przez piekarnik elektryczny pracujący pod napięciem 230 V. Oblicz moc piekarnika.
Wzór:
Dane:
Szukane:
Obliczenia:
Odpowiedź:
Moc piekarnika jest równa 690 W.
Żarówka o mocy 100 W jest włączona do sieci o napięciu 230 V. Oblicz natężenie prądu płynącego przez żarówkę. Jeśli żarówka zamienia 10% pobieranej energii na światło, to ile energii świetlnej emituje w czasie 1 sekundy?
Wzory:
Dane:
Szukane:
Obliczenia:
Odpowiedź:
Natężenie prądu płynącego przez żarówkę wynosi 0,43 A, a jej energia świetlna emitowana w ciągu 1 sekundy – 10 J.
Uzupełnij luki.
Grzałka elektryczna o mocy 1150 W podłączona jest do napięcia 230 V. Natężenie prądu płynącego przez grzałkę oraz ilość ciepła emitowanego przez grzałkę w czasie 0,5 minuty wynoszą odpowiednio:
I = ............ A
W = ............ kJ.
Spirala grzejna piekarnika o oporze jest zasilana z sieci domowej o napięciu . Oblicz moc grzałki w piekarniku.
Wzory:
Uwaga: Zadanie może być rozwiązane na dwa sposoby.
Dane:
Szukane:
Obliczenia – 1. sposób:
Obliczenia – 2. sposób:
Odpowiedź:
Moc grzałki w piekarniku jest równa 2 300 W.
Grzałka elektryczna o oporze 40 Ω jest zasilana ze źródła o napięciu 200 V.
Oceń prawdziwość zdań.
| Prawda | Fałsz | |
| Moc grzałki jest mniejsza niż 2000 W. | □ | □ |
| Natężenie prądu płynącego przez grzałkę jest równe 5 A. | □ | □ |
| Moc grzałki jest mniejsza niż 1000 W. | □ | □ |
Podsumowanie
Moc prądu elektrycznego (P) informuje o ilości energii elektrycznej (W) przekazanej elementowi obwodu elektrycznego w jednostce czasu (t):
Aby obliczyć moc prądu elektrycznego, napięcie elektryczne (U) mnożymy przez natężenie prądu elektrycznego (I).
Żarówki o parametrach 60 W, 230 V i 100 W, 230 V połączono szeregowo i dołączono do źródła prądu elektrycznego o napięciu 230 V. Oblicz moc pojedynczych żarówek oraz moc całego układu.
Elektryczny ogrzewacz wody o pojemności 10 litrów wyposażony jest w grzałkę o mocy 2,0 kW. Grzałka podłączona do źródła prądu o napięciu 230 V w ciągu 25 minut ogrzewa wodę o 60°C.
Oblicz opór grzałki.
Oblicz, ile ciepła zostanie przekazane otoczeniu podczas ogrzewania wody, przyjmując, że ciepło właściwe wody jest równe .
Zadania podsumowujące lekcję
Wybierz te odpowiedzi, które stanowią prawidłowe dokończenie zdania:
Energia elektryczna
- może zamienić się na energię chemiczną, mechaniczną lub ciepło.
- zamieni się na energię mechaniczną, gdy do obwodu elektrycznego podłączony zostanie silnik.
- może zamienić się na energię wewnętrzną prowadząc do wzrostu temperatury elementu obwodu elektrycznego np. opornika.
- zamienia się na ciepło, gdy do obwodu elektrycznego podłączony zostanie akumulator.
Uzupełnij puste miejsca, wykonując wcześniej potrzebne obliczenia. Wyniki zaokrąglij do części dziesiętnych.
Urządzenie: zasilacz do laptopa
U = 20 V
I = 4,5 A
P = ............ W
R = ............ Ω
Urządzenie: żelazko
U = 240 V
I = ............ A
P = 2400 W
R = ............ Ω
Uzupełnij puste miejsca.
Żelazko o mocy 2300 W jest zasilane z sieci domowej o napięciu równym 230 V. Ciepło emitowane przez żelazko w czasie 1 sekundy jest równe ............ J.
Jeśli prasowanie zajmie 5 minut, to żelazko wyemituje ............ J ciepła,
czyli ............ kJ.