Animacja 3D
Zapoznaj się z treścią animacji 3D. Zwróć uwagę na dowód twierdzenia Eulera i jego związek z diagramami Schlegela.
Zapoznaj się z opisem animacji 3D.
Film dostępny pod adresem https://zpe.gov.pl/a/D1ASpLfVP
Animacja 3D. Przyjrzymy się teraz twierdzeniu Eulera dla jednospójnych wielościanów wypukłych. Czyli takich wielościanów, które nie są wydrążone tunelami, a ich ściany nie przenikają się, tak jak w wielościanach gwiaździstych. Wówczas między liczbą wierzchołków, krawędzi i ścian takich wielościanów zachodzi równość: . W to oczywiście liczba wierzchołków, K to liczba krawędzi, S to liczba ścian. W przypadku czworościanu mamy 4 wierzchołki, 6 krawędzi oraz 4 ściany, czyli . W przypadku prostopadłościanu lub każdego innego graniastosłupa czworokątnego mamy 8 wierzchołków, 12 krawędzi i 6 ścian, czyli . Rozpatrzmy teraz przypadki negatywne oraz pozytywne zbudowane za pomocą czworościanu. Zacznijmy od przypadków negatywnych. Jeżeli zetkniemy dwa czworościany w jednym wierzchołku, to wówczas mamy 7 wierzchołków, liczba ścian to 8, a liczba krawędzi wynosi dwanaście. Obliczmy teraz: , czyli równanie nie zachodzi. Sprawdźmy co się stanie, jeśli skleimy dwa czworościany wzdłuż krawędzi podstawy, tak że podstawy nie leżą w jednej płaszczyźnie. Liczba wierzchołków wynosi 6, liczba ścian jest równa 8, natomiast liczba krawędzi wynosi jedenaście. Policzmy teraz: . Przejdźmy do przypadków pozytywnych. Złączmy teraz czworościany wierzchołkami, ale na nieco większej powierzchni trójkątnej. Sprawdźmy teraz: mamy 9 wierzchołków, 8 ścian i 15 krawędzi, czyli . Sklejmy teraz czworościany identycznymi ścianami. Otrzymamy spójną bryłę, która ma 5 wierzchołków, 6 ścian i 9 krawędzi, czyli . Wróćmy na moment do wypukłości brył, w przykładzie z łączeniem czworościanów wierzchołkami, obie figury nie są wypukłe, w jednym przypadku nie wzór działa, a w drugim tak. Tajemnica jest związana z miejscem sklejenia, jeżeli to jest jeden pojedynczy punkt albo krawędź to wzór nie będzie działać, a jeśli mamy sklejenie na przykład trójkątne to przykład zadziała. Dla ułatwienia możemy wyobrazić sobie, że próbujemy napompować balonik w figurze tak, żeby dotykał on każdej ściany. W przykładach negatywnych nie jest to możliwe, natomiast w przedstawionych przykładach pozytywnych jest to możliwe. Uzasadnijmy teraz wzór Eulera. Załóżmy, że mamy czworościan. Widok od góry. Wierzchołek rozdziela trzy trójkątne ściany boczne. Widok od dołu, przyjmując, że podstawa jest półprzeźroczysta. Utożsamiamy zewnętrze tego trójkąta z podstawą, mamy wówczas podstawę, trzy trójkątne ściany boczne, wszystkie krawędzie i wszystkie wierzchołki. Uzyskaliśmy w ten sposób tak zwany diagram Schlegela, w tym przypadku reprezentujący czworościan. Każdy wielościan wypukły ma taki diagram. Wszystkie diagramy spełniają wzór Eulera, chociaż nie wszystkie diagramy Schlegela mają swoje wielościany. Idea dowodu jest indukcyjna. Dołóżmy na jednej z krawędzi jeden wierzchołek do diagramu Schlegela czworościanu. Wzrasta liczba wierzchołków, ale też wzrasta liczba krawędzi. Powstały diagram spełnia wzór Eulera, choć nie ma bryły, którą ten diagram reprezentuje. Możliwe jest stworzenie diagramu Schlegela sześcianu oddając odpowiednią ilość krawędzi i wierzchołków do diagramu Schlegela czworościanu, w każdym kroku równanie Eulera jest spełnione. Skoro jesteśmy w stanie stworzyć diagram Schlegela sześcianu, to jesteśmy w stanie stworzyć diagram dowolnego wielościanu wypukłego.
Autor animacji 3D zwraca uwagę na to, kiedy wielościany, które nie są wypukłe, spełniają równość Eulera. Odwołując się do animacji, nie wykonując obliczeń, ustal i zaznacz, które z wielościanów poniżej nie spełnią równości .
- Opis poprawnej ilustracji A
- Opis ilustracji B
- Opis poprawnej ilustracji C

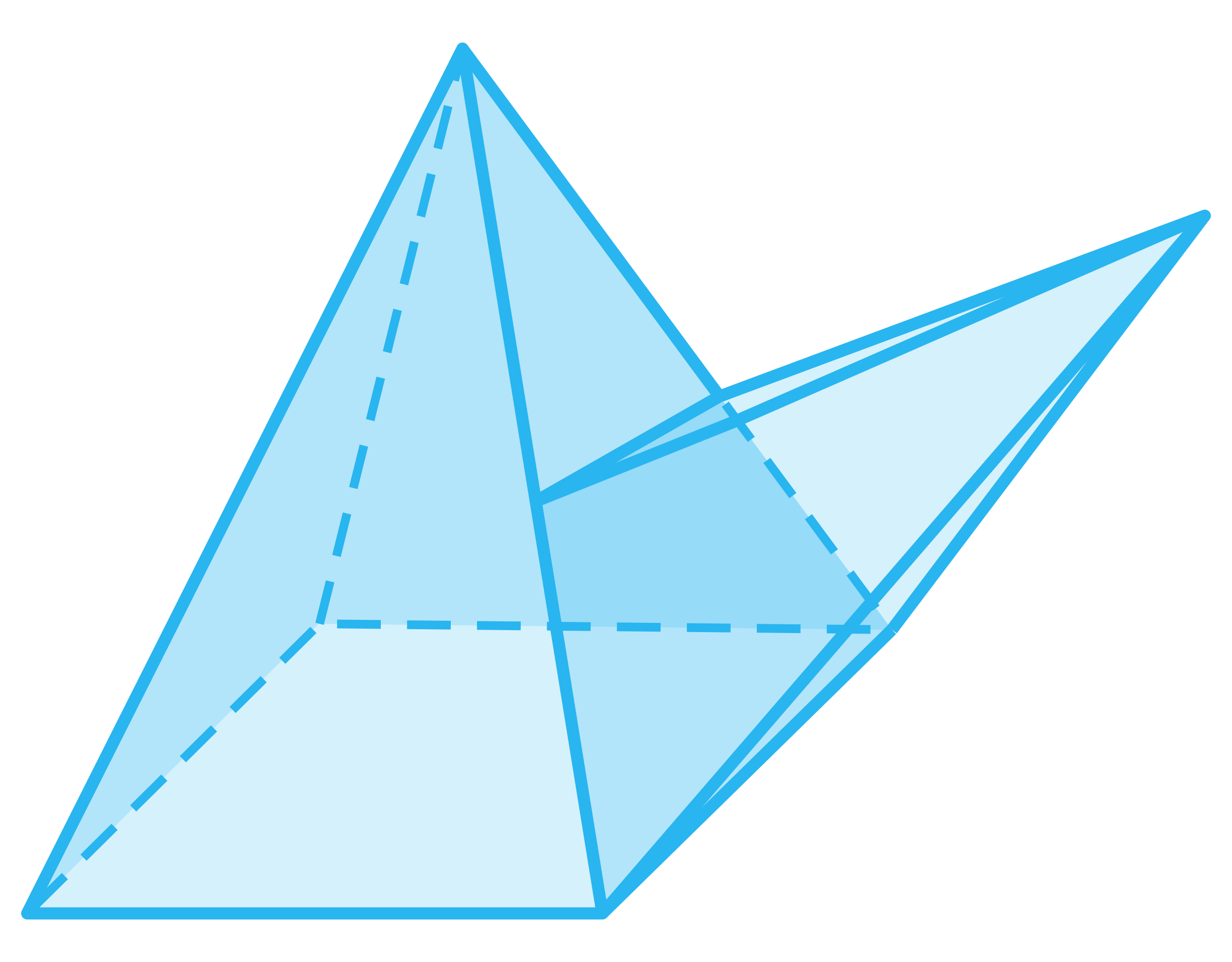

Odwołując się do animacji 3D, odpowiedz na pytanie. Który z wielościanów nie spełnia równania Eulera?
- Dwa czworościany połączone wierzchołkami
- Dwa czworościany połączone identycznymi ścianami
- Dwa czworościany połączone powierzchnią trójkątną