Powtórzenie wiadomości o figurach płaskich
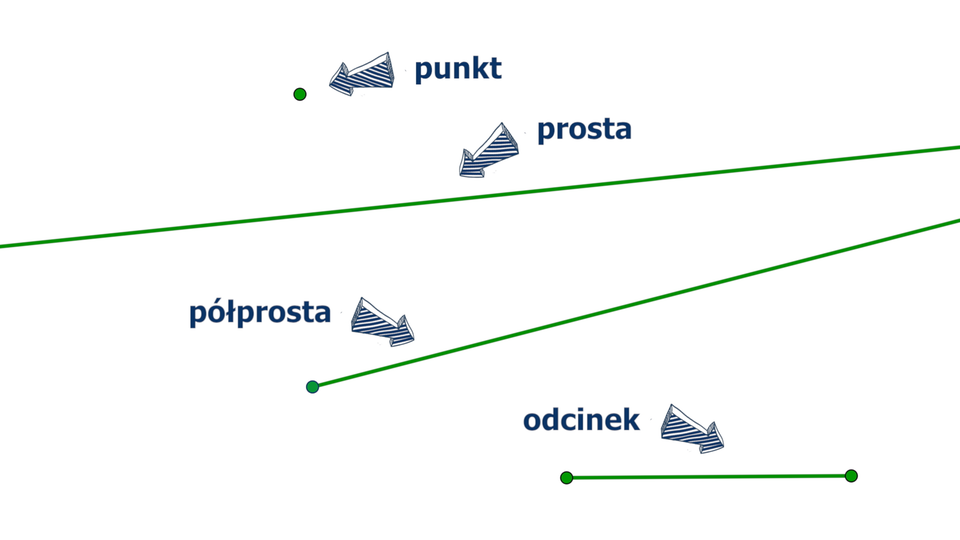
Punkt, odcinek, półprosta, prosta
Film dostępny na portalu epodreczniki.pl
Animacja
Narysuj
punkt oraz dwie proste prostopadłe przecinające się w tym punkcie.
dwie proste równoległe, oddalone od siebie o centymetry.
półprostą i punkt leżący na półprostej i oddalony od jej początku o .
dwa odcinki równoległe o długościach i .
Rozstrzygnij, które zdanie jest prawdziwe, a które fałszywe.
- Dwie proste, które nie są równoległe zawsze przecinają się w jednym punkcie.
- Przez dwa punkty może przejść tylko jedna prosta.
- Dwa nierównoległe odcinki muszą się przecinać.
- Dwa odcinki prostopadłe nie muszą się przecinać.
Kąty
Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.

Film dostępny na portalu epodreczniki.pl
Animacja
Rozstrzygnij, które zdanie jest prawdziwe, a które fałszywe.
- Każdy kąt ma wierzchołek i dwa ramiona.
- Kąt ostry ma więcej niż .
- Kąt prosty ma .
- Kąt rozwarty ma więcej niż i mniej niż .
- W kącie półpełnym ramiona kąta tworzą prostą.
- Ramiona kąta nie należą do tego kąta.
Dwie przecinające się proste utworzyły kąty i . Dana jest miara jednego z tych kątów. Oblicz miary trzech pozostałych, a następnie uzupełnij zdania.

Kąty i i i oraz i to pary kątów … .
Kąty i oraz i to pary kątów … .
Trójkąt, czworokąt i inne wielokąty
Policz, ile jest na rysunku wszystkich
trójkątów
trójkątów ostrokątnych
trójkątów prostokątnych
trójkątów rozwartokątnych
trapezów
czworokątów
równoległoboków
prostokątów
RiPepzfgnkgzm1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Wybierz.
przekątna, tym samym boku, dwa, trzy, cztery, wewnątrz, odcinek, prostą, dwa, trójkąt, dwa, cięciwa
Przekątną wielokąta nazywamy ............................ łączący ............................ wierzchołki wielokąta, które nie leżą na ............................ figury. Każda ............................ dzieli wielokąt na ............................ wielokąty, które mają w sumie o ............................ kąty więcej niż dany wielokąt.
Rozstrzygnij, które zdanie jest prawdziwe, a które fałszywe.
- Każdy wielokąt ma tyle samo kątów, ile boków.
- Żaden trójkąt nie ma przekątnych
- Kwadrat to prostokąt, który ma wszystkie boki tej samej długości.
- Każdy wielokąt o liczbie boków większej od ma więcej przekątnych niż boków.
- Trapez prostokątny równoramienny nazywa się prostokątem.
Który wielokąt opisujemy używając następujących słów:
przyprostokątna, przeciwprostokątna
wierzchołek, bok, przekątna
ramię, podstawa
kąt przy wierzchołku
obwód i pole
Dobierz stwierdzenie do podanego uzasadnienia.
Stwierdzenia
Każdy wielokąt ma tyle samo kątów, ile boków.
Żaden trójkąt nie ma przekątnych.
Przekątne kwadratu przecinają się pod kątem prostym.
Nie każdy wielokąt o liczbie boków większej od ma więcej przekątnych niż boków.
Trapez prostokątny równoramienny jest prostokątem.
Uzasadnienie
Trapez prostokątny równoramienny ma dwa boki tworzące z podstawami kąty proste.
Ramiona każdego kąta wielokąta zawierają dwa boki wielokąta.
Przekątne kwadratu dzielą go na trójkąty, w których dwa kąty mają po , wobec tego trzeci kąt ma .
Pięciokąt ma pięć przekątnych.
Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta i nie będący jego bokiem.
Koła i okręgi
Okręgiem nazywamy figurę złożoną ze wszystkich punktów płaszczyzny równo oddalonych od ustalonego punktu, zwanego środkiem okręgu.

Film dostępny na portalu epodreczniki.pl
Animacja
Kołem o środku w punkcie i promieniu nazywamy figurę zbudowaną ze wszystkich punktów płaszczyzny, których odległość od punktu jest mniejsza bądź równa promieniowi.

Film dostępny na portalu epodreczniki.pl
Animacja
Wybierz.
promień, dłuższa, cięciwa, promień, krótsza, promieniem, średnicą, średnica, cięciwa
a) Odcinek, którego końcami są środek okręgu i dowolny punkt leżący na okręgu, to .....................
b) Odcinek, którego końce leżą na okręgu to .....................
c) Najdłuższą cięciwę koła lub okręgu nazywamy .....................
d) Średnica jest dwa razy .................... od promienia koła lub okręgu.
Podano długości promieni: okręgu o środku w punkcie i okręgu o środku w punkcie . Jaką długość ma promień trzeciego okręgu? Uzupełnij tabelę.

