Prostokątny układ współrzędnych na płaszczyźnie
Geografowie określają położenie obiektów na kuli ziemskiej, korzystając z układu współrzędnych geograficznych, który wyznaczają południki, równoleżniki, równik i bieguny. Punkt zaznaczony na siatce geograficznej opisywany jest za pomocą pary liczb, nazywanej jego współrzędnymi geograficznymi. Pierwsza współrzędna to długość geograficzna, a druga – szerokość geograficzna. Punkt przecięcia południka zerowego z równikiem to początek układu współrzędnych.
Współrzędne punktu : długości geograficznej wschodniej, szerokości geograficznej północnej.
W zapisie międzynarodowym:
W praktyce do szybkiego wyznaczania położenia obiektu (nawet poruszającego się) wykorzystuje się najczęściej Globalny System Nawigacji (GPS), który obejmuje swym zasięgiem całą kulę ziemską. System ten jest ogólnodostępny, z jego usług może korzystać każda osoba, która posiada odpowiedni odbiornik.
Układy współrzędnych stosuje się również w wielu innych dziedzinach wiedzy, np. w geodezji, fizyce (do opisywania ruchu ciał).
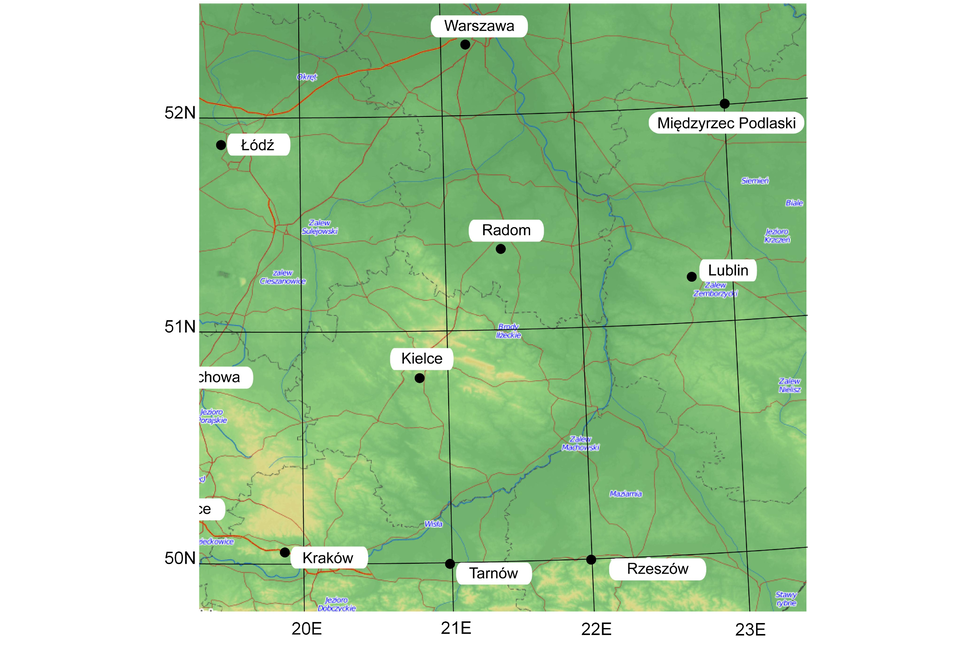
Odczytaj współrzędne geograficzne (szerokość i długość) następujących miejscowości:
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
Międzyrzec Podlaski,
Tarnów
Kraków
Kartezjański układ współrzędnych
W matematyce najczęściej posługujemy się układem współrzędnych, który tworzą dwie wzajemnie prostopadłe osie liczbowe. Punkt przecięcia tych prostych, nazywany jest początkiem układu współrzędnych.
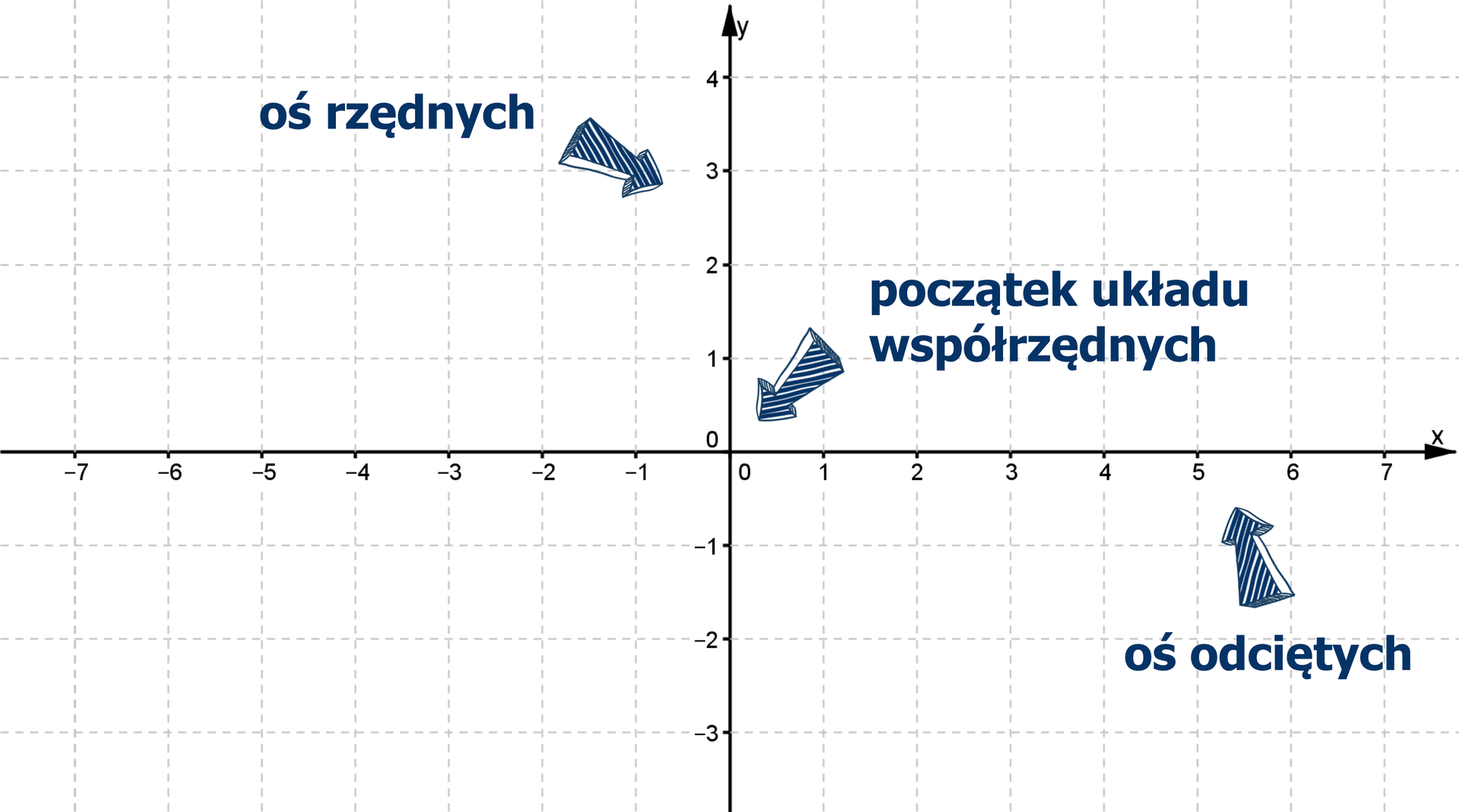
Oś pozioma (pierwsza oś) nazywana jest osią odciętych lub osią .
Oś pionowa (druga oś) nazywana jest osią rzędnych lub osią .
Prostokątny układ współrzędnych nazywany jest układem kartezjańskim od Kartezjusza (Rene Descartes’a), znakomitego siedemnastowiecznego francuskiego matematyka, przyrodnika i filozofa, którego uważa się za prekursora stosowania metod geometrycznych w zagadnieniach algebraicznych.
Powszechnie znana jest sentencja filozoficzna Kartezjusza „Myślę, więc jestem”.

Każdemu punktowi zaznaczonemu w układzie współrzędnych odpowiada uporządkowana para liczb nazywanych jego współrzędnymi.
Zapisujemy
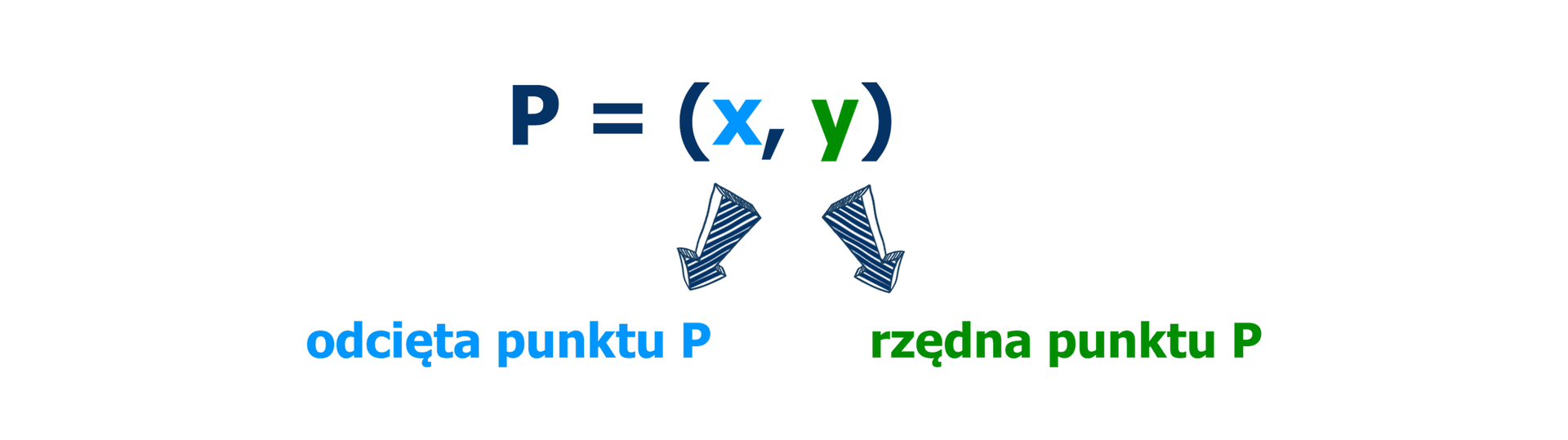
Pierwsza współrzędna określa położenie punktu względem osi , a druga – względem osi .
Aby wyznaczyć pierwszą współrzędną punktu , można zaznaczyć prostą prostopadłą do osi przechodzącą przez punkt . Liczba odpowiadająca punktowi, w którym ta prosta przecina oś , jest pierwszą współrzędną punktu – odciętą punktu .
Aby wyznaczyć drugą współrzędną punktu , można zaznaczyć prostą prostopadłą do osi przechodzącą przez punkt . Liczba odpowiadająca punktowi, w którym ta prosta przecina oś , jest drugą współrzędną punktu – rzędną punktu .

Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
Najczęściej na obu osiach układu współrzędnych obieramy jednakowe jednostki tak, aby można było zaznaczyć dane punkty.
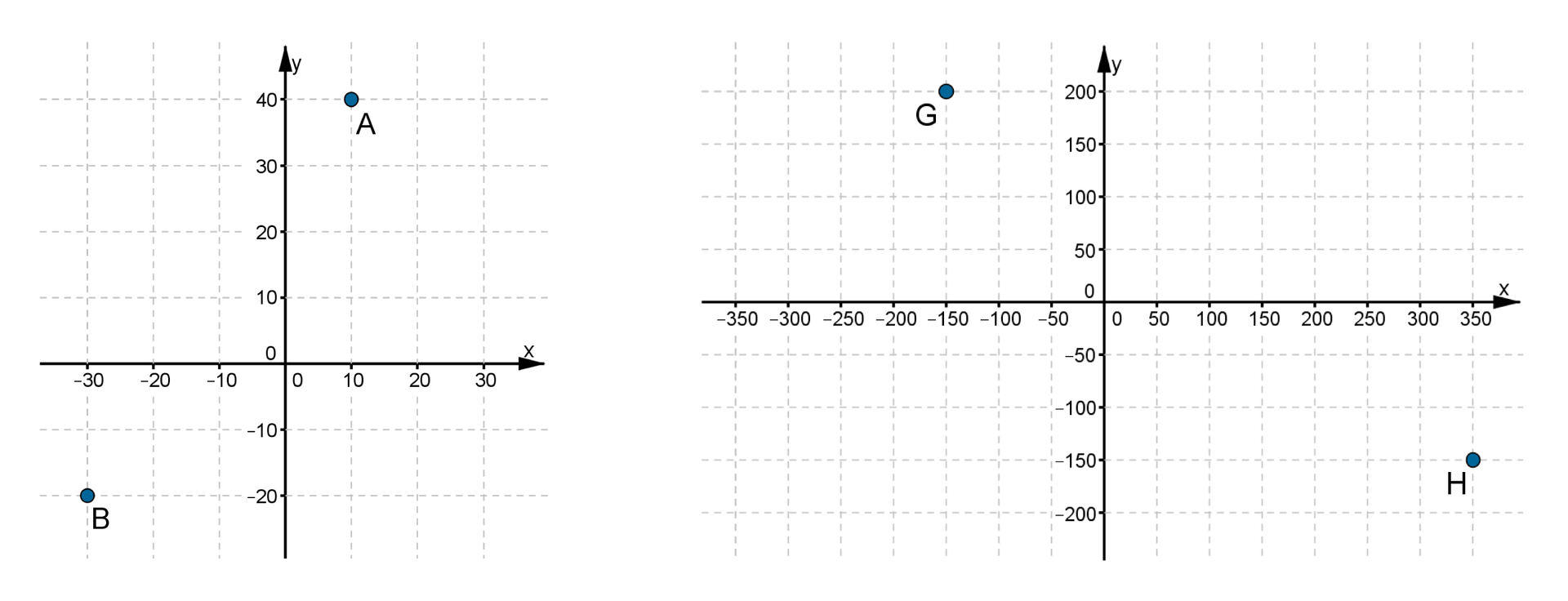
W zastosowaniach praktycznych, gdy na osiach układu współrzędnych zaznaczane są różne wielkości, jednostki mogą mieć różne długości.
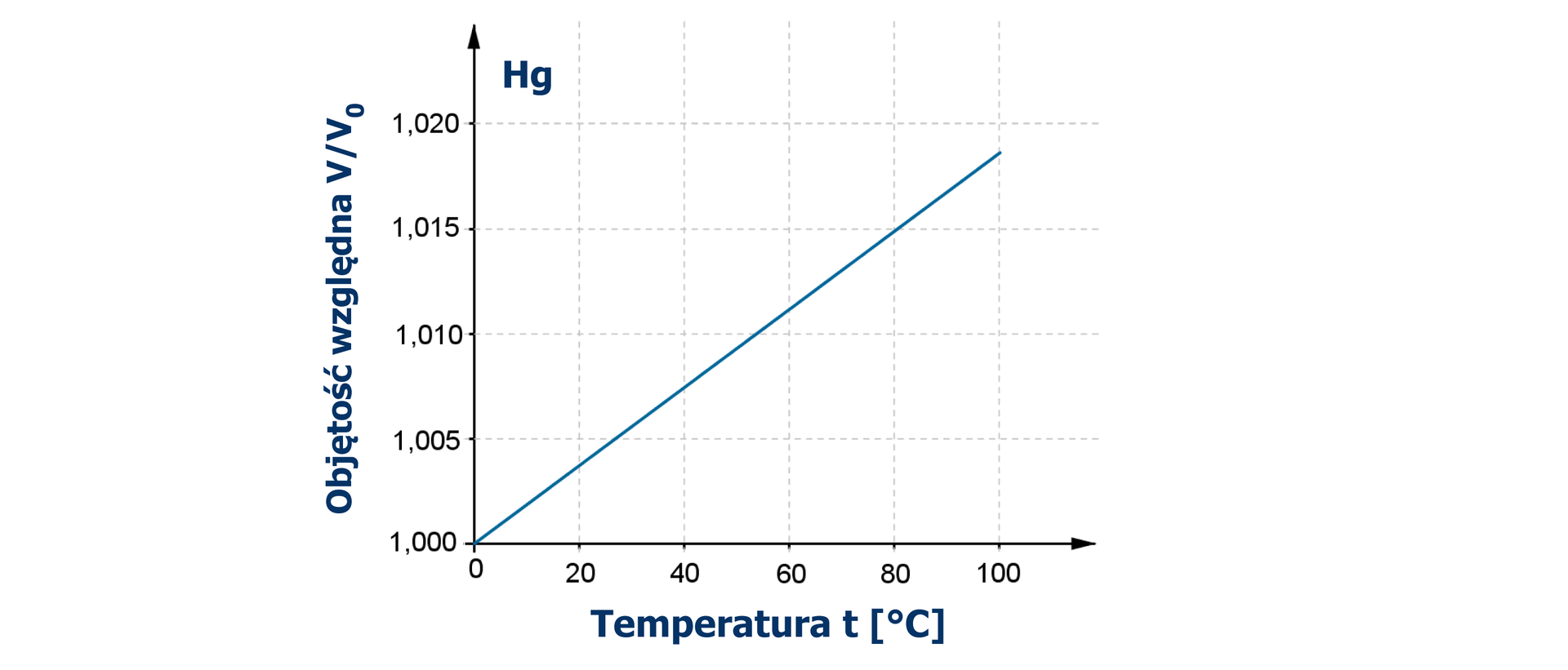
Wykres zmiany objętości rtęci w zależności od temperatury.
W układzie współrzędnych zaznaczone są punkty leżące na osiach układu.

Odczytajmy ich współrzędne.
Punkty leżące na osi :
Punkty leżące na osi :
Zauważmy, że
punkty leżące na osi mają drugą współrzędną równą
punkty leżące na osi mają pierwszą współrzędną równą
Początek układu współrzędnych (punkt ) ma współrzędne .
Podaj współrzędne punktu .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
W układzie współrzędnych ustaw punkt tak, aby miał dane współrzędne.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
Ćwiartki układu współrzędnych
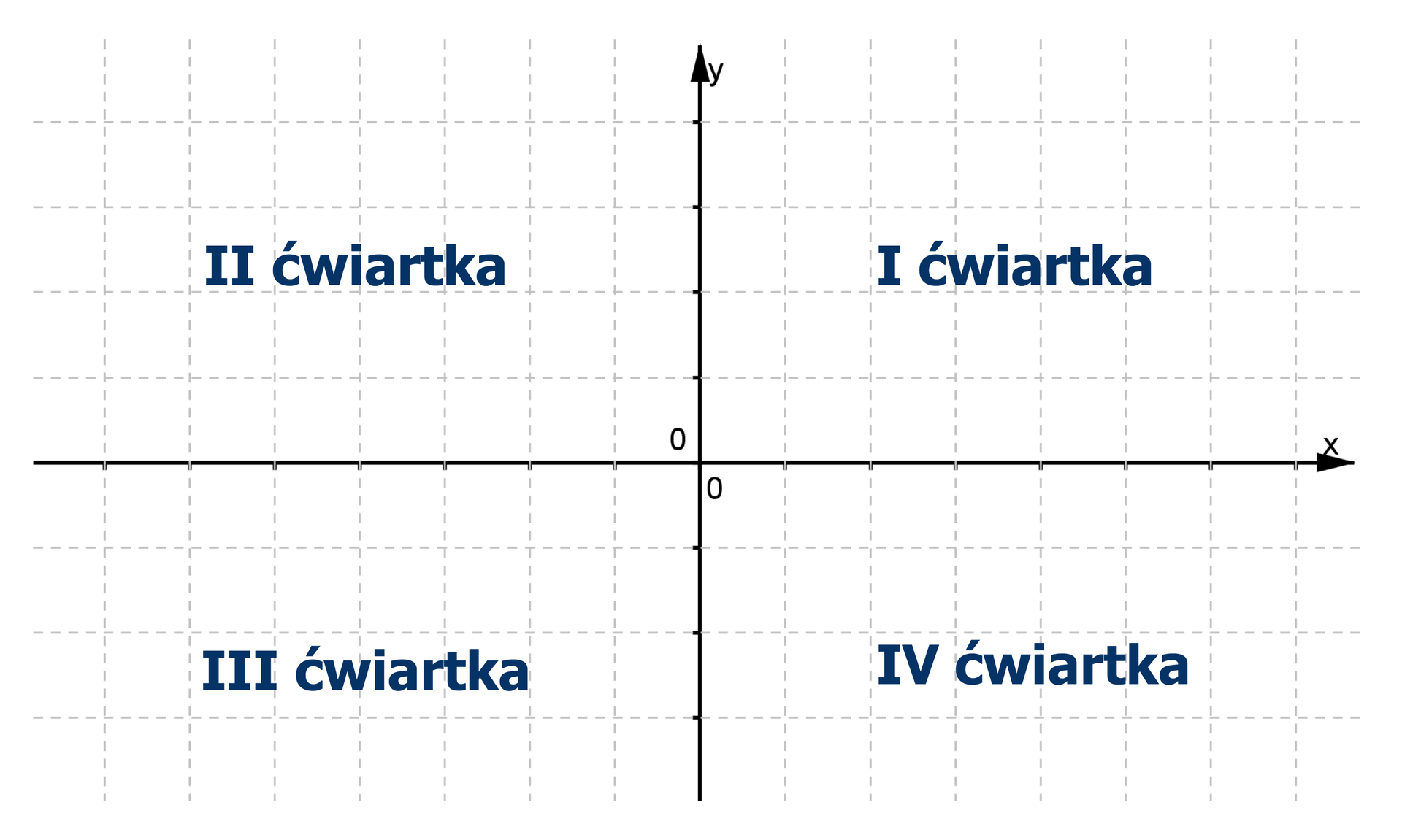
Osie układu współrzędnych dzielą płaszczyznę na cztery części nazywane ćwiartkami.
Ćwiartki numerujemy: I, II, III, IV przeciwnie do ruchu wskazówek zegara.
Punktów leżących na osiach układu współrzędnych nie zaliczamy do żadnej ćwiartki.
Zmieniaj położenie punktu zaznaczonego w układzie współrzędnych.
Zaobserwuj znaki pierwszej oraz drugiej współrzędnej punktu w poszczególnych ćwiartkach układu współrzędnych.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
Jeżeli punkt należy do:
ćwiartki układu współrzędnych, to obie jego współrzędne są liczbami dodatnimi,
ćwiartki układu współrzędnych, to jego pierwsza współrzędna jest liczbą ujemną, a druga dodatnią,
ćwiartki układu współrzędnych, to obie jego współrzędne są liczbami ujemnymi.
ćwiartki układu współrzędnych, to jego pierwsza współrzędna jest liczbą dodatnią, a druga ujemną.
R1b3msZGOj2nr1 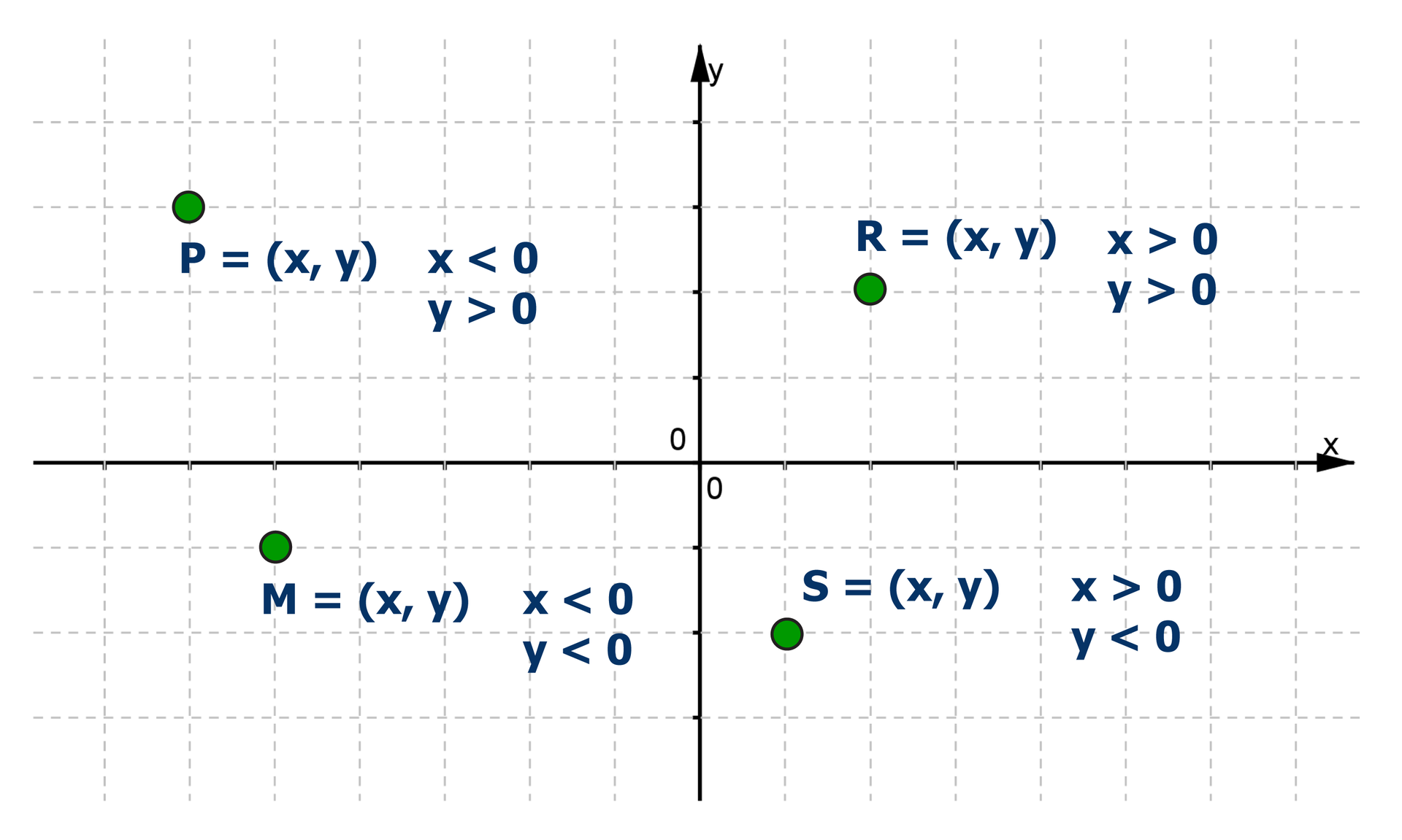 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
Narysuj układ współrzędnych, dobierz odpowiednio jednostkę i zaznacz punkty i .
Podaj współrzędne punktu .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
Punkt znajduje się w układzie współrzędnych na osi odciętych, gdy
Jeżeli punkt znajduje się na osi , to
Znajdź liczbę wiedząc, że
punkt leży na osi .
punkt leży na osi
Przeciągnij punkty do odpowiedniej ćwiartki układu współrzędnych.
<span aria-label="H, równa się, nawias trzysta dwanaście przecinek jeden trzy dwa zamknięcie nawiasu" role="math"><math><mi>H</mi><mo>=</mo><mo>(</mo><mn>312</mn><mo>,</mo><mn>132</mn><mo>)</mo></math></span>, <span aria-label="C, równa się, nawias, minus, dwadzieścia trzy, przecinek, minus, trzydzieści trzy zamknięcie nawiasu" role="math"><math><mi>C</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>23</mn><mo>,</mo><mo>-</mo><mn>33</mn><mo>)</mo></math></span>, <span aria-label="F, równa się, nawias, minus, osiemset dziewięć przecinek dziewięć zamknięcie nawiasu" role="math"><math><mi>F</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>809</mn><mo>,</mo><mn>9</mn><mo>)</mo></math></span>, <span aria-label="I, równa się, nawias dziesięć, przecinek, minus, jeden zamknięcie nawiasu" role="math"><math><mi>I</mi><mo>=</mo><mo>(</mo><mn>10</mn><mo>,</mo><mo>-</mo><mn>1</mn><mo>)</mo></math></span>, <span aria-label="B, równa się, nawias, minus, dwadzieścia sześć przecinek jeden osiem siedem zamknięcie nawiasu" role="math"><math><mi>B</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>26</mn><mo>,</mo><mn>187</mn><mo>)</mo></math></span>, <span aria-label="A, równa się, nawias dwanaście przecinek trzy dwa zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mn>12</mn><mo>,</mo><mn>32</mn><mo>)</mo></math></span>, <span aria-label="E, równa się, nawias sto, przecinek, minus, siedemset sześćdziesiąt pięć zamknięcie nawiasu" role="math"><math><mi>E</mi><mo>=</mo><mo>(</mo><mn>100</mn><mo>,</mo><mo>-</mo><mn>765</mn><mo>)</mo></math></span>, <span aria-label="G, równa się, nawias, minus, dziewięćdziesiąt jeden, przecinek, minus, trzy zamknięcie nawiasu" role="math"><math><mi>G</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>91</mn><mo>,</mo><mo>-</mo><mn>3</mn><mo>)</mo></math></span>, <span aria-label="D, równa się, nawias, minus, trzysta sześćdziesiąt pięć przecinek dwa zamknięcie nawiasu" role="math"><math><mi>D</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>365</mn><mo>,</mo><mn>2</mn><mo>)</mo></math></span>
| I ćwiartka | |
|---|---|
| II ćwiartka | |
| III ćwiartka | |
| IV ćwiartka |
W której ćwiartce układu współrzędnych leży punkt ?

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsGqD5YZu
Jeżeli punkt znajduje się w ćwiartce układu współrzędnych, to liczba może być równa
Punkt znajduje się w drugiej ćwiartce układu współrzędnych.
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Tak, ponieważ odcięta jest liczbą ujemną
- Nie, ponieważ odcięta jest liczbą ujemną
- Tak, ponieważ rzędna jest liczbą ujemną.
- Nie, ponieważ obie współrzędne są ujemne.
- Tak, ponieważ obie współrzędne są ujemne.
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Punkty i mają taką samą rzędną.
- Punkty i znajdują się na osi odciętych.
Zaznacz w układzie współrzędnych cztery różne punkty , z których każdy znajduje się w innej ćwiartce układu współrzędnych. Odczytaj współrzędne tych punktów i uzupełnij tabelkę.
Nazwa punktu | Pierwsza współrzędna punktu | Druga współrzędna punktu | Numer ćwiartki układu współrzędnych, w której znajduje się punkt |
Zaznacz w układzie współrzędnych taki punkt
którego obie współrzędne są równe
którego druga współrzędna jest o mniejsza od pierwszej
którego pierwsza współrzędna jest dwukrotnie większa od drugiej
Zaznacz w układzie współrzędnych punkty . Co powiesz o ich wzajemnym położeniu?
Punkty skrajne Polski

Najdalej na północ wysunięty kraniec Polski o współrzędnych – miejscowość Jastrzębia Góra w gminie Władysławowo, powiat pucki.
Najdalej na południe wysunięty kraniec Polski – szczyt Opołonek w gminie Lutowiska, powiat bieszczadzki.
Najdalej na zachód wysunięty kraniec Polski – kolano Odry koło Osinowa Dolnego w gminie Cedynia, powiat gryfiński.
Najdalej na wschód wysunięty kraniec Polski – kolano Bugu we wsi Zosin w gminie Horodło, powiat hrubieszowski.
Środek geometryczny Polski znajduje się we wsi Piątek, na wschód od Łęczycy, na południe od Kutna, a na północ od Łodzi.
Oblicz różnicę czasu słonecznego między skrajnymi punktami Polski wschodnim i zachodnim.
W Szczecinie jest godzina w południe czasu słonecznego. Która godzina czasu słonecznego jest wtedy w Lublinie?
W Warszawie czas słoneczny określany jest według południka . Jaka jest różnica czasu słonecznego między Warszawą a Rzeszowem?
Określ współrzędne geograficzne środka Polski.
Jednym z najbardziej tajemniczych miejsc na ziemi jest Trójkąt Bermudzki.
Określ współrzędne geograficzne wierzchołków tego trójkąta i dowiedz się, czym się charakteryzuje ten obszar.