Przeczytaj

W tej części lekcji poznamy wiadomości o różnych przekątnych graniastosłupa prawidłowego sześciokątnego.

Przekątne podstawy graniastosłupa prawidłowego sześciokątnego, czyli przekątne sześciokąta foremnego

R14CpfcFnhaUF

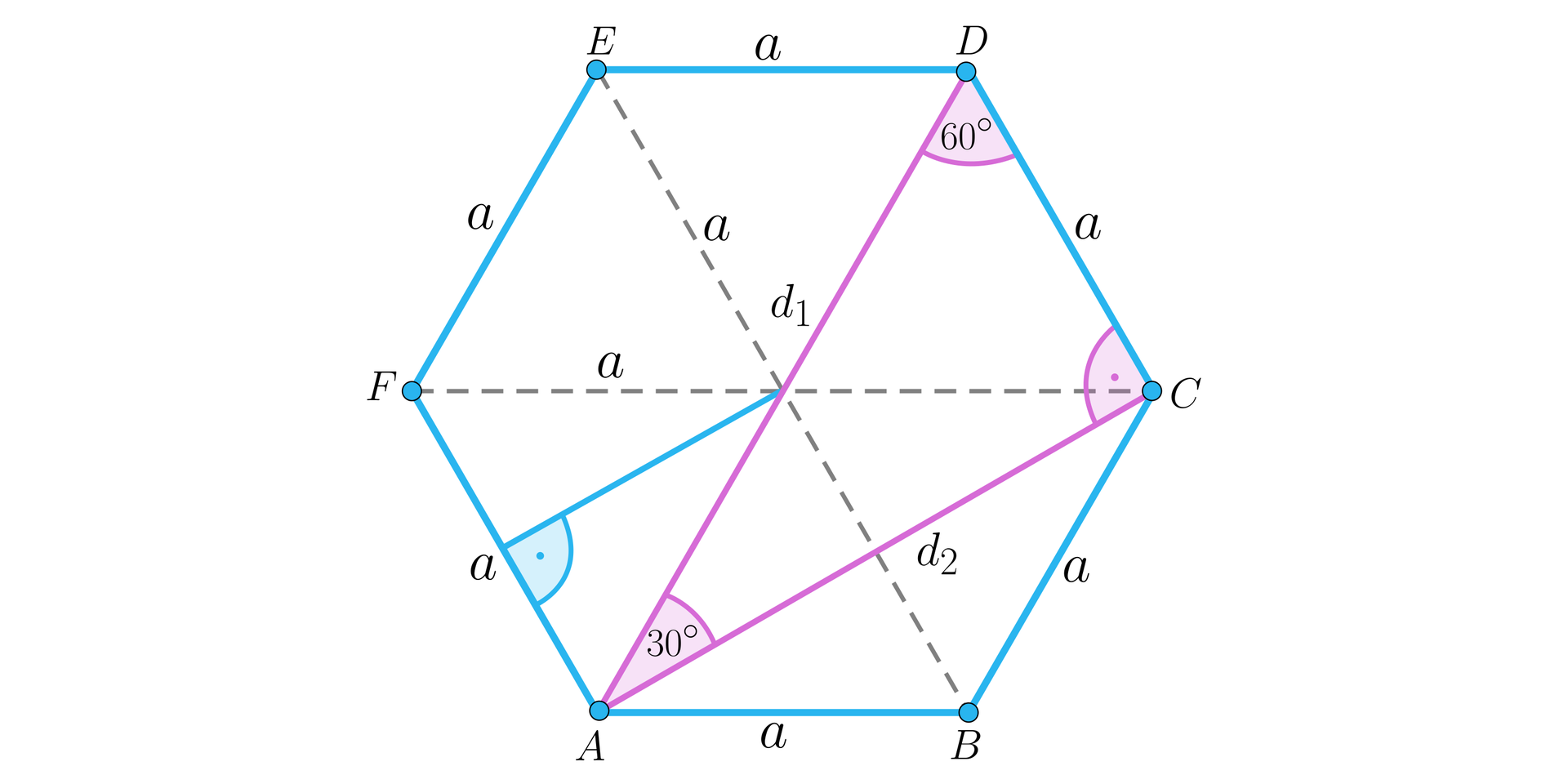
Na ilustracji przedstawiono sześciokąt foremny ABCDEF, o boku długości a, oraz środku w punkcie O. Zaznaczono trzy przekątne dłuższe, oznaczone d1, oraz sześć przekątnych krótszych, oznaczonych d2. Przekątne dłuższe to A D przecinek B E przecinek C F. Do przekątnych krótszych należą A C przecinek, A E przecinek C E przecinek D F przecinek D B przecinek F B. Zaznaczono trójkąt ACD o przyprostokątnych a, d2, oraz przeciwprostokątnej d1. Kąt ACD=90°, kąt ADC=60°, kąt DAC=30°. Zaznaczono trójkąt równoboczny AFO, oraz wysokość opuszczoną na podstawę AF.

Widzimy dwa rodzaje przekątnych:
$d_{1}$ – dłuższą przekątną, równą $d_{1} = 2 \cdot a$ ,
$d_{2}$ – krótszą przekątną, równą $d_{2} = 2 \cdot h_{△} = 2 \cdot \frac{a \sqrt{3}}{2} = a \sqrt{3}$ .

Zauważmy, że można wyróżnić trzy przekątne dłuższe:
$d_{1} = |A D| = |B E| = |C F|$
oraz sześć przekątnych krótszych:
$d_{2} = |A C| = |A E| = |C E| = |D F| = |D B| = |F B|$ .

Przekątne ścian bocznych graniastosłupa prawidłowego sześciokątnego

W ścianach bocznych tego wielokąta foremnegowielokąt foremnywielokąta foremnego znajduje się sześć przystających prostokątów. Obie przekątne prostokąta mają równe długości oznaczone na rysunku literą $d$ .

R1cvlAoCy3Ztn

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o podstawie dolnej ABCDEF, oraz górnej GHIJKL. Krawędź graniastosłupa oznaczono a. Zaznaczono trójkąt BGH, o przyprostokątnych a, h oraz przeciwprostokątnej d. Kąt GHA=90°.

Bardzo prosto, stosując jedynie twierdzenie Pitagorasa do wyróżnionego trójkąta, możemy wyznaczyć wzór na przekątną ściany bocznej, w zależności od krawędzi podstawy i jego wysokości:

d = \sqrt{a^{2} + h^{2}}

oraz po jego przekształceniu:

wzór na krawędź podstawy: $a = \sqrt{d^{2} - h^{2}}$ , gdzie $d > h$ ,

wzór na wysokość: $h = \sqrt{d^{2} - a^{2}}$ , gdzie $d > a$ .

Oczywiście zakładamy, że $a > 0$ , $h > 0$ oraz $d > 0$ .

Przekątne graniastosłupa prawidłowego sześciokątnego

W graniastosłupie prawidłowym sześciokątnym mamy dwa rodzaje przekątnych różnej długości.

Na początek zajmiemy się dłuższą przekątną, oznaczoną na rysunku $D_{1}$ .

R18BlJYFFn0Ed

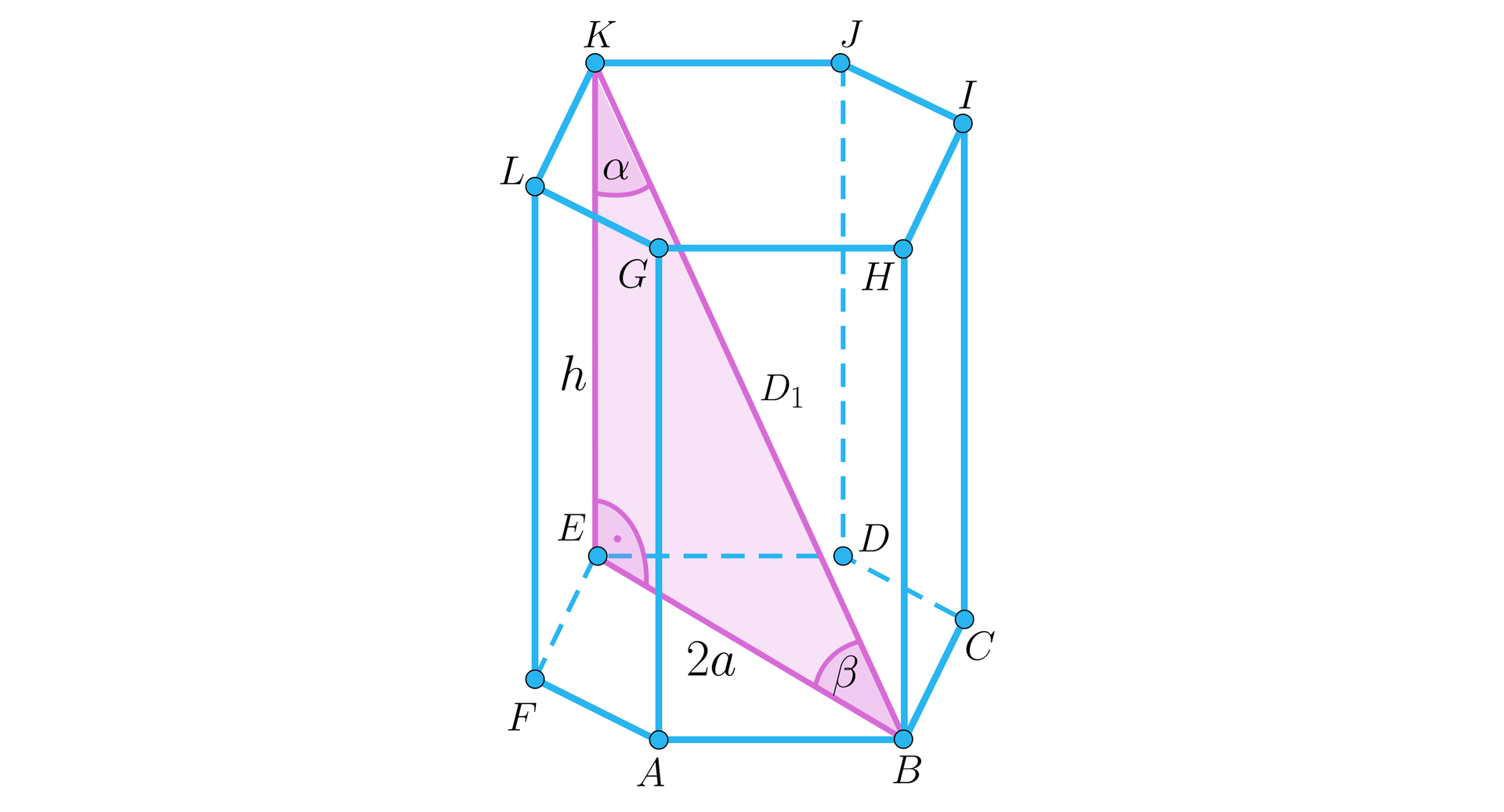
Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o podstawie dolnej ABCDEF, oraz górnej kolejno GHIJKL, i wysokości h. Zaznaczono przekątną bryły K B oznaczoną wielka litera D indeks dolny jeden koniec indeksu, oraz dłuższą przekątną dolnej podstawy E B równą 2 a. Zaznaczono trójkąt prostokątny BEK, o przyprostokątnych h, czyli E K oraz 2 a, czyli E B, oraz przeciwprostokątnej, wielka litera D indeks dolny jeden koniec indeksu, czyli K B. Przy wierzchołku K zaznaczono kąt α, przy wierzchołku B zaznaczono kąt β, natomiast kąt przy wierzchołku E jest kątem prostym.

Stosując twierdzenie Pitagorasa do wyróżnionego trójkąta, możemy wyznaczyć wzór na przekątną $D_{1}$ w zależności od krawędzi podstawy i jego wysokości:

D_{1}

= \sqrt{{(2 a)}^{2} + h^{2}}

Ostatecznie otrzymujemy:

D_{1}

= \sqrt{4 a^{2} + h^{2}}

Oczywiście $a > 0$ , $h > 0$ oraz $D_{1} > 0$ .

Oraz po jego przekształceniu:

wzór na krawędź podstawy: $a = \frac{1}{2} \sqrt{{D_{1}}^{2} - h^{2}}$ , gdzie $D_{1} > h$ ,

wzór na wysokość: $h = \sqrt{{D_{1}}^{2} - 4 a^{2}}$ , gdzie $D_{1} > 2 a$ .

Spójrzmy teraz na krótszą przekątną, oznaczoną na rysunku $D_{2}$ .

RSpm0ntILjERN

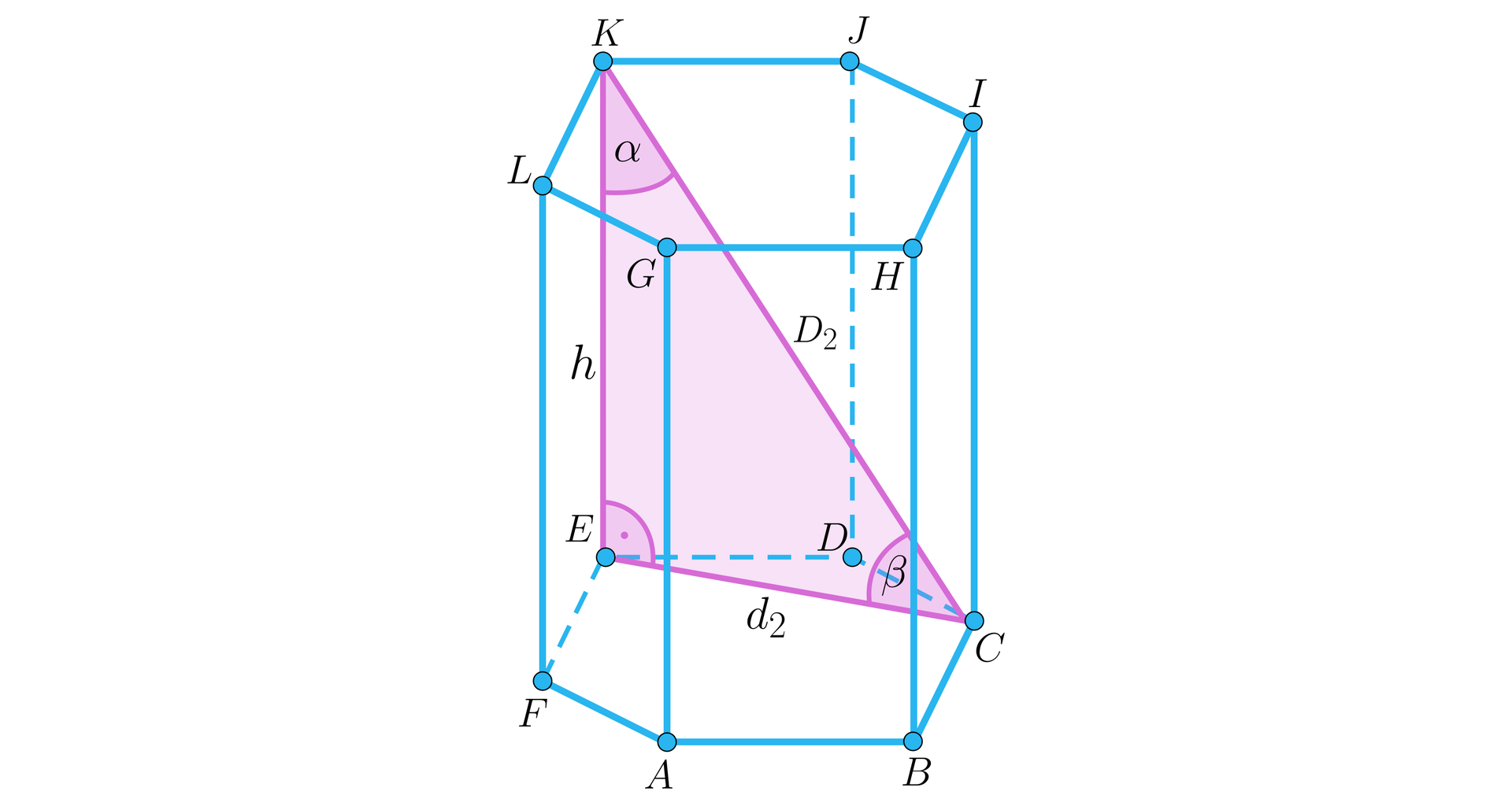
Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o podstawie dolnej ABCDEF, oraz górnej odpowiednio GHIJKL, i wysokości h, oznaczonej jako krawędź E K. Zaznaczono przekątną bryły oznaczoną wielka litera D indeks dolny dwa koniec indeksu, czyli odcinek C K, oraz krótszą dolnej podstawy oznaczoną d2, czyli odcinek E C. Zaznaczono trójkąt prostokątny ECK, o przyprostokątnych d2, czyli E C oraz h, czyli odcinek E K, oraz przeciwprostokątnej wielka litera D indeks dolny dwa koniec indeksu, czyli odcinek K C. Przy wierzchołku K zaznaczono kąt α, przy wierzchołku C zaznaczono kąt β, natomiast kąt przy wierzchołku E jest kątem prostym.

Stosując twierdzenie Pitagorasa do wyróżnionego trójkąta, możemy wyznaczyć wzór na przekątna $D_{2}$ w zależności od krawędzi podstawy i jego wysokości:

D_{2} = \sqrt{{(d_{2})}^{2} + h^{2}}

D_{2} = \sqrt{{(a \sqrt{3})}^{2} + h^{2}}

Ostatecznie otrzymujemy:

D_{2} = \sqrt{3 a^{2} + h^{2}}

Oczywiście $a > 0$ , $h > 0$ oraz $D_{2} > 0$

oraz po jego przekształceniu:

wzór na krawędź podstawy: $a = \frac{\sqrt{3}}{3} \sqrt{{D_{2}}^{2} - h^{2}}$ , gdzie $D_{2} > h$ ,

wzór na wysokość: $h = \sqrt{{D_{2}}^{2} - 3 a^{2}}$ , gdzie $D_{2} > a \sqrt{3}$ .

Masz do dyspozycji aplet GeoGebry, za pomocą którego możesz obejrzeć omawiane odcinki w modelu graniastosłupa, możesz też obracać modelem i zmieniać kąt widzenia.

Zapoznaj się z poniższym opisem apletu GeoGebry, w którym przedstawiono omawiane odcinki w modelu graniastosłupa.

RkmwQyO6xzFiH

Przykład 1

Mając dane długości przekątnych $D_{1}$ oraz $D_{2}$ w graniastosłupie prawidłowym sześciokątnym, wyznacz jego wymiary.

Przyjmiemy, że $D_{1} > D_{2}$ .

Znamy długości obu przekątnych graniastosłupa, więc możemy wstawić dane do wzorów:
$D_{1} = \sqrt{4 a^{2} + h^{2}}$ i $D_{2}$ $= \sqrt{3 a^{2} + h^{2}}$ .

Przekształcając, otrzymujemy:
$\{\begin{cases} {D_{1}}^{2} = 4 a^{2} + h^{2} \\ {D_{2}}^{2} = 3 a^{2} + h^{2} \end{cases}$ .

Odejmując stronami równania, mamy:
${D_{1}}^{2} - {D_{2}}^{2} = a^{2}$ .

Czyli długość krawędzi wynosi:
$a = \sqrt{{D_{1}}^{2} - {D_{2}}^{2}}$ .

Wyznaczymy teraz długość wysokości $h$ podstawiając na przykład do równania:
$D_{2}$ $= \sqrt{3 a^{2} + h^{2}}$
${D_{2}}^{2}$ $= 3 a^{2} + h^{2}$
${D_{2}}^{2} = 3 ({D_{1}}^{2} - {D_{2}}^{2}) + h^{2}$
${D_{2}}^{2} = 3 {D_{1}}^{2} - 3 {D_{2}}^{2} + h^{2}$
$h^{2} = 3 {D_{2}}^{2} - 3 {D_{1}}^{2} + {D_{2}}^{2}$
$h^{2} = 4 {D_{2}}^{2} - 3 {D_{1}}^{2}$
$h = \sqrt{4 {D_{2}}^{2} - 3 {D_{1}}^{2}}$ .

Uwzględniając dziedzinę pierwiastka, pojawia się dodatkowe założenie $D_{1} < \frac{2}{3} \sqrt{3} D_{2}$ .

Odpowiedź: Wymiary tego graniastosłupa wynoszą: krawędź podstawy $a = \sqrt{{D_{1}}^{2} - {D_{2}}^{2}}$ , natomiast wysokość $h = \sqrt{4 {D_{2}}^{2} - 3 {D_{1}}^{2}}$ , przy założeniu $D_{2} < D_{1} < \frac{2}{3} \sqrt{3} D_{2}$ .

Przykład 2

W graniastosłupie prawidłowym sześciokątnym dwie przekątne różnej długości bryły wychodzące z jednego wierzchołka oraz krawędź podstawy o długości a utworzyły trójkąt. Wyznacz kąty w tym trójkącie, jeżeli wysokość graniastosłupa jest równa $k \cdot a$ , dla $k \in \{1, 2, 3, 4, 5\}$ .

RAxiLxYxRdgzq

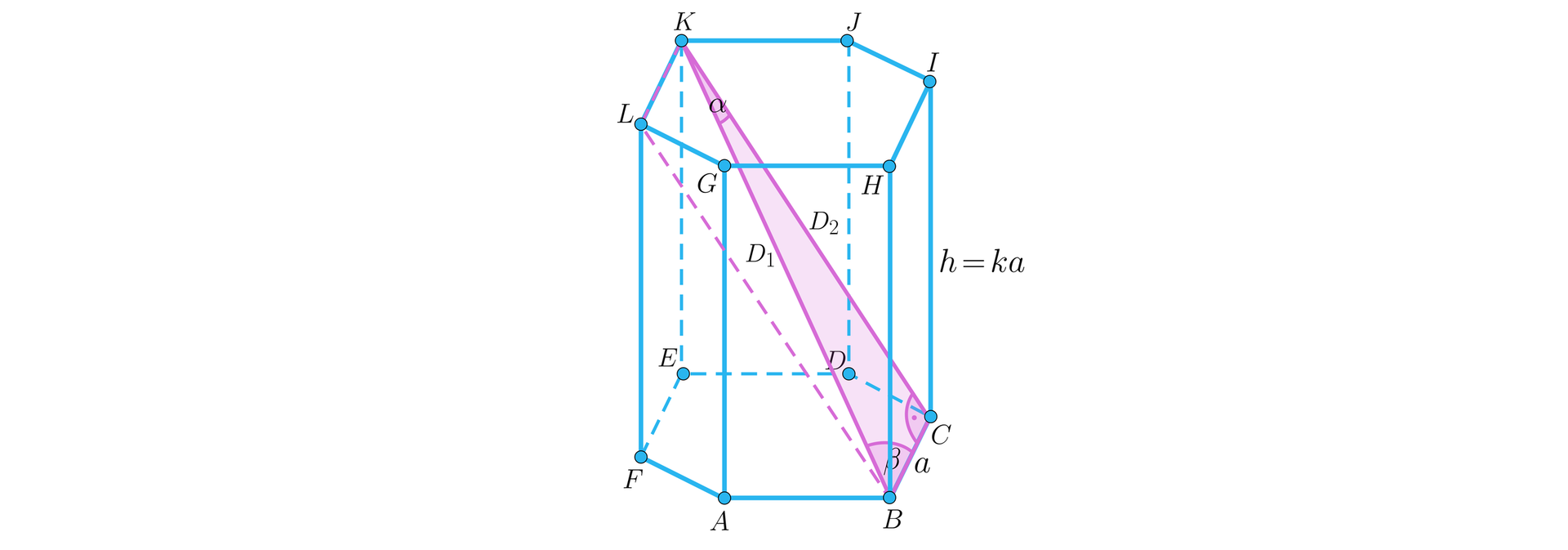
Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o podstawie dolnej ABCDEF, oraz górnej odpowiednio GHIJKL. Krawędź podstawy oznaczono literą a, natomiast wysokość literą h. Wysokość jest równa k×a. Linią przerywaną zaznaczono odcinek L B będący krótszą przekątną bryły. Kolorem różowym zamalowano trójkąt prostokątny BCK, o przyprostokątnych stanowiących krawędź B C dolnej podstawy i krótszą przekątną bryły C K graniastosłupa. Odcinek ten oznaczono wielką literą D z indeksem dolnym dwa. Przeciwprostokątna trójkąta K B, to dłuższa przekątna bryły. Odcinek K B oznaczono wielką literą D o indeksie jeden. W trójkącie zaznaczono kąty wewnętrzne. Kąt przy wierzchołku B wynosi β, kąt przy wierzchołku K wynosi α, kąt przy wierzchołku C jest kątem prostym.

Wyznaczymy długość przekątnej $D_{1}$ :

$D_{1}$ $= \sqrt{4 a^{2} + h^{2}} = \sqrt{4 a^{2} + {(k a)}^{2}} = \sqrt{4 a^{2} + k^{2} a^{2}} =$
$= \sqrt{(4 + k^{2}) a^{2}} = a \sqrt{4 + k^{2}}$ ,

Przekątna $D_{1}$ jest jednocześnie przekątną prostokąta $B C K L$ , więc wyróżniony na rysunku trójkąt jest prostokątny. Chcąc znać jego kąty posługujemy się funkcjami trygonometrycznymi, sinus kąta $α$ sin alfa (sinus kąta alfa)sinus kąta $α$ jest równy:

\sin α = \frac{a}{a \sqrt{4 + k^{2}}} = \frac{1}{\sqrt{4 + k^{2}}}

kąt	$k = 1$	$k = 2$	$k = 3$	$k = 4$	$k = 5$
$\sin α$	$\frac{1}{\sqrt{4 + 1^{2}}} = \frac{1}{\sqrt{5}} \approx 0, 4472$	$\frac{1}{\sqrt{4 + 2^{2}}} = \frac{1}{2 \sqrt{2}} \approx 0, 3536$	$\frac{1}{\sqrt{4 + 3^{2}}} = \frac{1}{\sqrt{13}} \approx 0, 2774$	$\frac{1}{\sqrt{4 + 4^{2}}} = \frac{1}{2 \sqrt{5}} \approx 0, 2236$	$\frac{1}{\sqrt{4 + 5^{2}}} = \frac{1}{\sqrt{29}} \approx 0, 1857$
$α$	$\approx 27 °$	$\approx 21 °$	$\approx 16 °$	$\approx 13 °$	$\approx 11 °$
$β = 90 ° - α$	$\approx 63 °$	$\approx 69 °$	$\approx 74 °$	$\approx 77 °$	$\approx 79 °$

Przykład 3

Różnica długości przekątnych graniastosłupaprzekątna graniastosłupaprzekątnych graniastosłupa prawidłowego sześciokątnego zbudowanego wyłącznie z figur foremnych wynosi $c$ , gdzie $c > 0$ . Jaka jest długość krawędzi tego graniastosłupa?

RC7DM83c4mh4h

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny. Krawędź podstawy ma długość a, wysokość bryły wynosi h równe a. W bryle wykreślono przekątną krótszą oznaczoną wielką literą D z indeksem 2 oraz dłuższą przekątną bryły oznaczoną wielką literą D z indeksem jeden. Kolorem wyróżniono trójkąt prostokątny, w którym przyprostokątne to boki: dolna krawędź a, przekątna krótsza bryły wielka litera D z indeksem dolnym 2 oraz z przeciwprostokątną wielka litera D indeks dolny jeden.

Badany graniastosłup jest zbudowany wyłącznie z figur foremnych, więc jego ściany są kwadratami, czyli wysokość jest równa krawędzi podstawy. Utworzony trójkąt jest prostokątny, stąd otrzymujemy:
$D_{1}$ $= \sqrt{4 a^{2} + a^{2}} = a \sqrt{5}$ i $D_{2}$ $= \sqrt{3 a^{2} + a^{2}} = 2 a$

Różnica przekątnych wynosi $c$ , stąd otrzymujemy:
$D_{1} - D_{2}$ $= c$
$a \sqrt{5} - 2 a = c$
$a (\sqrt{5} - 2) = c ∣ \cdot (\sqrt{5} + 2)$
$a (5 - 4) = c (\sqrt{5} + 2)$
$a = c (\sqrt{5} + 2)$ .

Odpowiedź: Krawędzie tego graniastosłupa mają długość $a = c (\sqrt{5} + 2)$ .

Przykład 4

Suma długości krawędzi graniastosłupa prawidłowego sześciokątnego wynosi $288 \sqrt{3} + 132$ . Wyznacz długości przekątnych tego graniastosłupa, jeżeli jego wysokość ma długość $22$ .

R1Tr8GtMpV4vB

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny. Krawędź podstawy ma długość a, wysokość bryły wynosi h równe dwadzieścia dwa. W bryle wykreślono przekątną krótszą oznaczoną wielką literą D z indeksem 2 oraz dłuższą przekątną bryły oznaczoną wielką literą D z indeksem jeden. Kolorem wyróżniono trójkąt prostokątny, w którym przyprostokątne to boki: dolna krawędź a, przekątna krótsza bryły wielka litera D z indeksem dolnym 2 oraz z przeciwprostokątną wielka litera D indeks dolny jeden.

Znamy krawędź boczną graniastosłupa oraz sumę krawędzi, więc
$S_{k} = 12 \cdot a + 6 \cdot h$
podstawiając wyznaczamy długość krawędzi podstawy:
$288 \sqrt{3} + 132 = 12 \cdot a + 6 \cdot 22$
$288 \sqrt{3} = 12 \cdot a ∣ : 12$
$24 \sqrt{3} = a$ .

Szukamy przekątnych:
$D_{1}$ $= \sqrt{4 a^{2} + h^{2}} = \sqrt{4 {(24 \sqrt{3})}^{2} + 22^{2}} =$
$= \sqrt{6912 + 484} = \sqrt{7396} = 86$ ,

$D_{2}$ $= \sqrt{3 a^{2} + h^{2}} = \sqrt{3 {(24 \sqrt{3})}^{2} + 22^{2}} =$
$= \sqrt{5184 + 484} = \sqrt{5668} = 2 \sqrt{1417}$ .

Odpowiedź: Szukane przekątne mają długości $D_{1} = 86$ , $D_{2}$ $= 2 \sqrt{1417}$ .

Słownik

przekątna graniastosłupa

każdy odcinek, którego końcami są wierzchołki obu podstaw graniastosłupa i który nie zawiera się w żadnej ze ścian graniastosłupa

wielokąt foremny

wielokąt, który ma wszystkie boki równe i wszystkie kąty równe

sin (sinus kąta alfa)

w trójkącie prostokątnym jest równy stosunkowi długości przyprostokątnej naprzeciw tego kąta do długości przeciwprostokątnej

Wprowadzenie

Animacja 3D

Przekątne podstawy graniastosłupa prawidłowego sześciokątnego, czyli przekątne sześciokąta foremnego

Przekątne ścian bocznych graniastosłupa prawidłowego sześciokątnego

Przekątne graniastosłupa prawidłowego sześciokątnego

Słownik