Zapiszemy równanie okręguokrągokręgu o środku w punkcie $\left(1,3\right)$ i przechodzącego przez punkt $A=\left(4,6\right)$.

Rozwiązanie:

Ponieważ środek okręgu znajduje się w punkcie $\left(1,3\right)$, to korzystając z równania ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$, możemy zapisać:

${\left(x-1\right)}^2+{\left(y-3\right)}^2=r^2$.

Punkt $A=\left(4, 6\right)$ należy do okręgu opisanego równaniem ${\left(x-1\right)}^2+{\left(y-3\right)}^2=r^2$, czyli jego współrzędne spełniają równanie tego okręgu.

Wyznaczamy promień okręgu.

${\left(4-1\right)}^2+{\left(6-3\right)}^2=r^2$

$r^2=3^2+3^2$

$r^2=9+9$

$r^2=18$

Równanie okręgu ma zatem postać: ${\left(x-1\right)}^2+{\left(y-3\right)}^2=18$.

Napiszemy równanie okręgu o promieniu $r=\sqrt{20}$ i przechodzącego przez punkty $A=\left(-3,1\right)$ i $B=\left(5,1\right)$.

Rozwiązanie:

Promień okręgu wynosi $r=\sqrt{20}$, więc korzystając z równania ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$, otrzymujemy

${\left(x-a\right)}^2+{\left(y-b\right)}^2=20$.

Jeżeli punkty $A=\left(-3,1\right)$ i $B=\left(5,1\right)$ należą do okręgu o równaniu ${\left(x-a\right)}^2+{\left(y-b\right)}^2=20$, to ich współrzędne spełniają równanie tego okręgu.

$\left\{\begin{array}{l}{\left(-3-a\right)}^2+{\left(1-b\right)}^2=20\\ {\left(5-a\right)}^2+{\left(1-b\right)}^2=20\end{array}\right.$

Z porównania lewych stron tych równań otrzymujemy

${\left(-3-a\right)}^2+{\left(1-b\right)}^2={\left(5-a\right)}^2+{\left(1-b\right)}^2$,

co po zastosowaniu wzoru skróconego mnożenia prowadzi do równania

$9+6a+a^2-\left(25-10a+a^2\right)=0$.

Kontynuując przekształcenia otrzymujemy kolejno

$9+6a+a^2-25+10a-a^2=0$,

$16a-16=0$,

stąd

$a=1$.

Aby wyznaczyć $b$, podstawiamy $a=1$ do równania ${\left(5-a\right)}^2+{\left(1-b\right)}^2=20$.

${\left(5-1\right)}^2+{\left(1-b\right)}^2=20$

$4^2+1-2b+b^2=20$

Otrzymujemy równanie kwadratowe.

$b^2-2b-3=0$

Wyróżnik trójmianu kwadratowego wynosi

$\Delta ={\left(-2\right)}^2-4·1·\left(-3\right)=4+12=16>0$,

więc równanie ma dwa rozwiązania:

$b_1=\frac{-\left(-2\right)+\sqrt{16}}{2·1}=\frac{2+4}{2}=3$ oraz $b_2=\frac{-\left(-2\right)-\sqrt{16}}{2·1}=\frac{2-4}{2}=-1$.

Istnieją dwa okręgi o promieniu $r=\sqrt{20}$, przechodzące przez punkty $A=\left(-3,1\right)$ i $B=\left(5,1\right)$. Ich równania są następujące:

${\left(x-1\right)}^2+{\left(y-3\right)}^2=20$ oraz ${\left(x-1\right)}^2+{\left(y+1\right)}^2=20$.

Napiszemy równanie okręgu o promieniu $r=2$ i stycznego do obu osi układu współrzędnych.

Rozwiązanie:

Jeżeli okrąg o promieniu $r=2$ jest styczny do obu osi układu współrzędnych, oznacza to, że odległość jego środka od każdej osi wynosi $2$. Istnieją cztery takie okręgi, a ich środki położone są w punktach:

$\left(2,2\right)$, $\left(-2,2\right)$, $\left(-2,-2\right)$ i $\left(2,-2\right)$.

RNDQrk6UYWGFU

Grafika przedstawia układ współrzędnych z poziomą osią x od minus czterech do czterech i pionową osią y od minus czterech do czterech. Na płaszczyźnie znajdują się cztery okręgi. Pierwszy z nich ma środek w punkcie początek nawiasu, 2, 2, zamknięcie nawiasu i jest styczny do osi y oraz osi x. Okrąg ten znajduje się w całości w pierwszej ćwiartce. Drugi z nich ma środek w punkcie początek nawiasu, minus 2, 2, zamknięcie nawiasu i jest styczny do osi y oraz osi x. Okrąg ten znajduje się w całości w drugiej ćwiartce. Trzeci z nich ma środek w punkcie początek nawiasu, minus 2, minus 2, zamknięcie nawiasu i jest styczny do osi y oraz osi x. Okrąg ten znajduje się w całości w trzeciej ćwiartce. Czwarty z nich ma środek w punkcie początek nawiasu, 2, minus 2, zamknięcie nawiasu i jest styczny do osi y oraz osi x. Okrąg ten znajduje się w całości w czwartej ćwiartce.

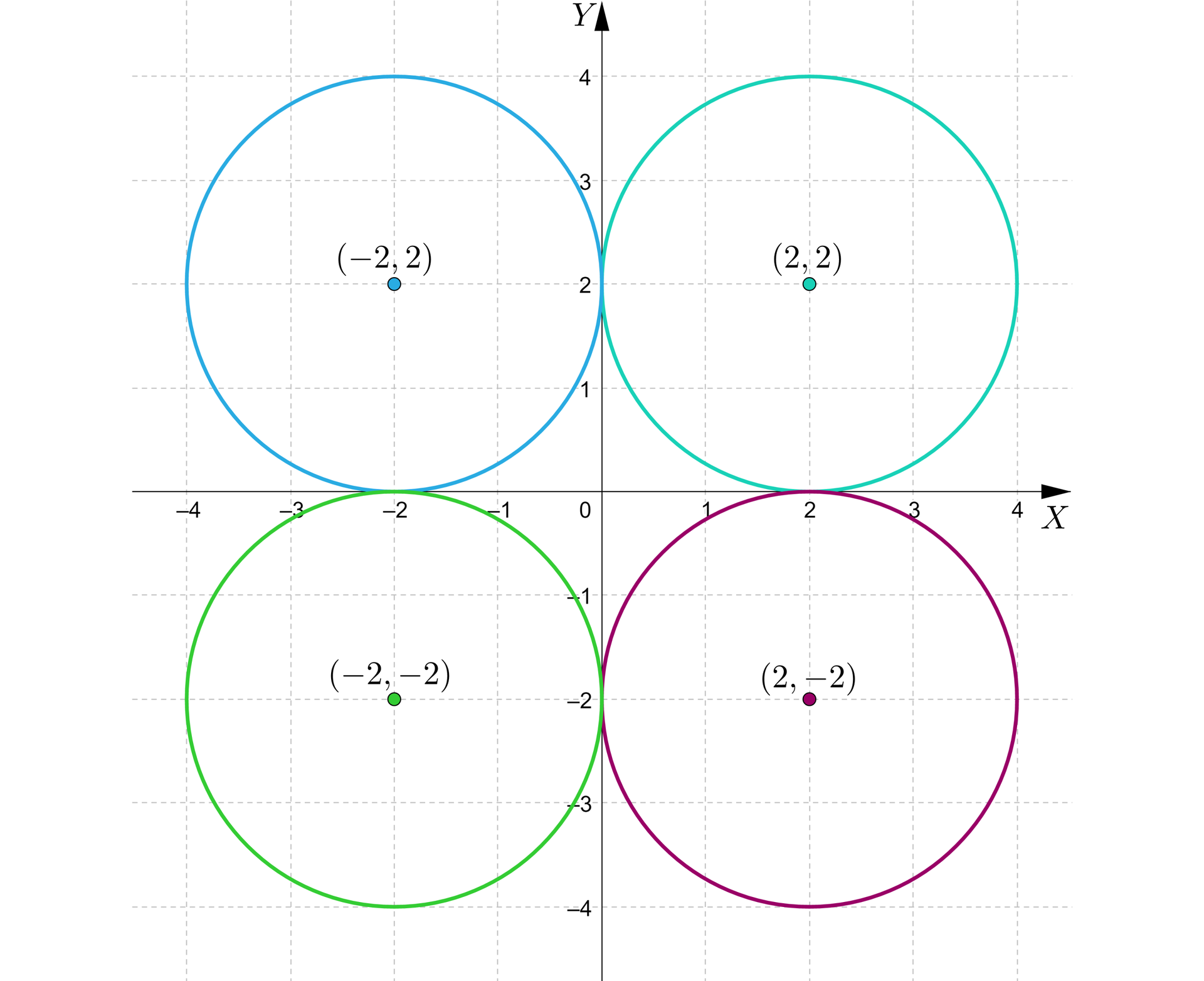
Równania okręgów spełniających warunki zadania są postaci:

${\left(x-2\right)}^2+{\left(y-2\right)}^2=4$,

${\left(x+2\right)}^2+{\left(y-2\right)}^2=4$,

${\left(x+2\right)}^2+{\left(y+2\right)}^2=4$,

${\left(x-2\right)}^2+{\left(y+2\right)}^2=4$.

Wyznaczymy równanie okręgu, do którego należą punkty wspólne wykresów funkcji $y=x^2-5x+6$ i $y=x+1$, wiedząc, że jego środek należy do prostej $y=-\frac{7}{3}x+3$.

Rozwiązanie:

Aby znaleźć punkty wspólne krzywych $y=x^2-5x+6$ i $y=x+1$, rozwiązujemy układ równań.

$\left\{\begin{array}{l}y=x^2-5x+6\\ y=x+1\end{array}\right.$

Po przyrównaniu stronami, otrzymujemy

$x^2-5x+6=x+1$

i ostatecznie równanie kwadratowe postaci

$x^2-6x+5=0$.

Wyróżnik trójmianu kwadratowego wynosi

$\Delta ={\left(-6\right)}^2-4·1·5=36-20=16>0$,

więc równanie ma dwa rozwiązania:

$x_1=\frac{-\left(-6\right)+\sqrt{16}}{2·1}=\frac{6+4}{2}=5$ oraz $x_2=\frac{-\left(-6\right)-\sqrt{16}}{2·1}=\frac{6-4}{2}=1$.

Ponieważ $y=x+1$, to dla $x_1=5$ mamy $y_1=6$, a dla $x_2=1$ mamy $y_2=2$.

Otrzymaliśmy punkty wspólne krzywych: $A=\left(5,6\right)$ i $B=\left(1,2\right)$.

Punkty te należą do okręgu ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$, czyli spełniają warunek: $\left|OA\right|=\left|OB\right|$.

Środek okręgu $O$ należy do prostej $y=-\frac{7}{3}x+3$, zatem

$O=\left(a,b\right)=\left(a,-\frac{7}{3}a+3\right)$.

Wyznaczymy teraz współrzędne środka okręgu $O=\left(a,b\right)$, wykorzystując warunek $\left|OA\right|=\left|OB\right|$.

Odległość punktów $A=\left(x_1,y_1\right)$, oraz $B=\left(x_2,y_2\right)$ wyraża się wzorem $\left|AB\right|=\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}$, zapisujemy:

$\left|OA\right|=\sqrt{{\left(x_A-x_S\right)}^2+{\left(y_A-y_S\right)}^2}$

$\left|OA\right|=\sqrt{{\left(5-a\right)}^2+{\left[6-\left(-\frac{7}{3}a+3\right)\right]}^2}$

$\left|OA\right|=\sqrt{{\left(5-a\right)}^2+{\left(3+\frac{7}{3}a\right)}^2}$

oraz

$\left|OB\right|=\sqrt{{\left(x_B-x_S\right)}^2+{\left(y_B-y_S\right)}^2}$

$\left|OB\right|=\sqrt{{\left(1-a\right)}^2+{\left[2-\left(-\frac{7}{3}a+3\right)\right]}^2}$

$\left|OB\right|=\sqrt{{\left(1-a\right)}^2+{\left(\frac{7}{3}a-1\right)}^2}$.

Z warunku $\left|OA\right|=\left|OB\right|$, otrzymujemy

$\sqrt{{\left(5-a\right)}^2+{\left(3+\frac{7}{3}a\right)}^2}=\sqrt{{\left(1-a\right)}^2+{\left(\frac{7}{3}a-1\right)}^2}$.

Po podniesieniu obu stron równości do kwadratu, równanie przyjmuje postać

${\left(5-a\right)}^2+{\left(3+\frac{7}{3}a\right)}^2={\left(1-a\right)}^2+{\left(\frac{7}{3}a-1\right)}^2$.

Korzystając ze wzorów skróconego mnożenia, doprowadzamy równość do postaci

$25-10a+a^2+9+14a+\frac{49}{9}{a}^2=1-2a+a^2+1-\frac{14}{3}a+\frac{49}{9}{a}^2$.

Po redukcji wyrażeń podobnych, otrzymujemy

$\frac{32}{3}a=-32$.

Stąd $a=-3$, a ponieważ $b=-\frac{7}{3}a+3$, to

$b=-\frac{7}{3}·\left(-3\right)+3=10$.

Środek okręgu leży w punkcie $O=\left(-3,10\right)$.

Otrzymaliśmy równanie okręgu postaci

${\left(x+3\right)}^2+{\left(y-10\right)}^2=r^2$,

a ponieważ $r=\left|OA\right|$, to

$r=\left|OA\right|=\sqrt{{\left(5+3\right)}^2+{\left(6-10\right)}^2}=\sqrt{64+16}=\sqrt{80}$.

Równanie okręgu jest postaci ${\left(x+3\right)}^2+{\left(y-10\right)}^2=80$.

Napisz równanie okręgu zawierającego punkty $A=\left(0,0\right)$ i $B=\left(1,7\right)$, którego środek leży na prostej $y=-x+7$.

Rozwiązanie:

Okrąg zawiera dwa punkty $A$ i $B$, więc jego środek leży na symetralnej odcinkasymetralna odcinkasymetralnej odcinka $AB$. Ponieważ leży on również na prostej $y=-x+7$, więc środek okręgu leży w punkcie przecięcia obu tych prostych. Obrazuje to poniższy rysunek.

R1byrFZCIixUP

Grafika przedstawia układ współrzędnych z poziomą osią x od minus jeden do siedmiu i pionową osią y od minus jeden do siedmiu. Na płaszczyźnie znajdują się trzy proste oraz dwa punkty. Punkt A ma współrzędne początek nawiasu, 0, 0, zamknięcie nawiasu, punkt B ma współrzędne początek nawiasu, 1, 7, zamknięcie nawiasu. Pierwsza ukośna prosta przechodzi zarówno przez punkt A i punkt B. Prosta ta ma równanie $y=7x$ . Druga ukośna prosta jest przechodzi przez punkt początek nawiasu, 0, 7, zamknięcie nawiasu oraz początek nawiasu, 7, 0, zamknięcie nawiasu i jest podpisana $y=-x+7$. Trzecia ukośna prosta została narysowana linią przerywaną i przecina oś y między wartością 3 i 4, następnie przecina pierwszą prostą i kolejno drugą prostą w punkcie początek nawiasu, 4, 3, zamknięcie nawiasu. Prosta ta jest podpisana $S_{AB}$.

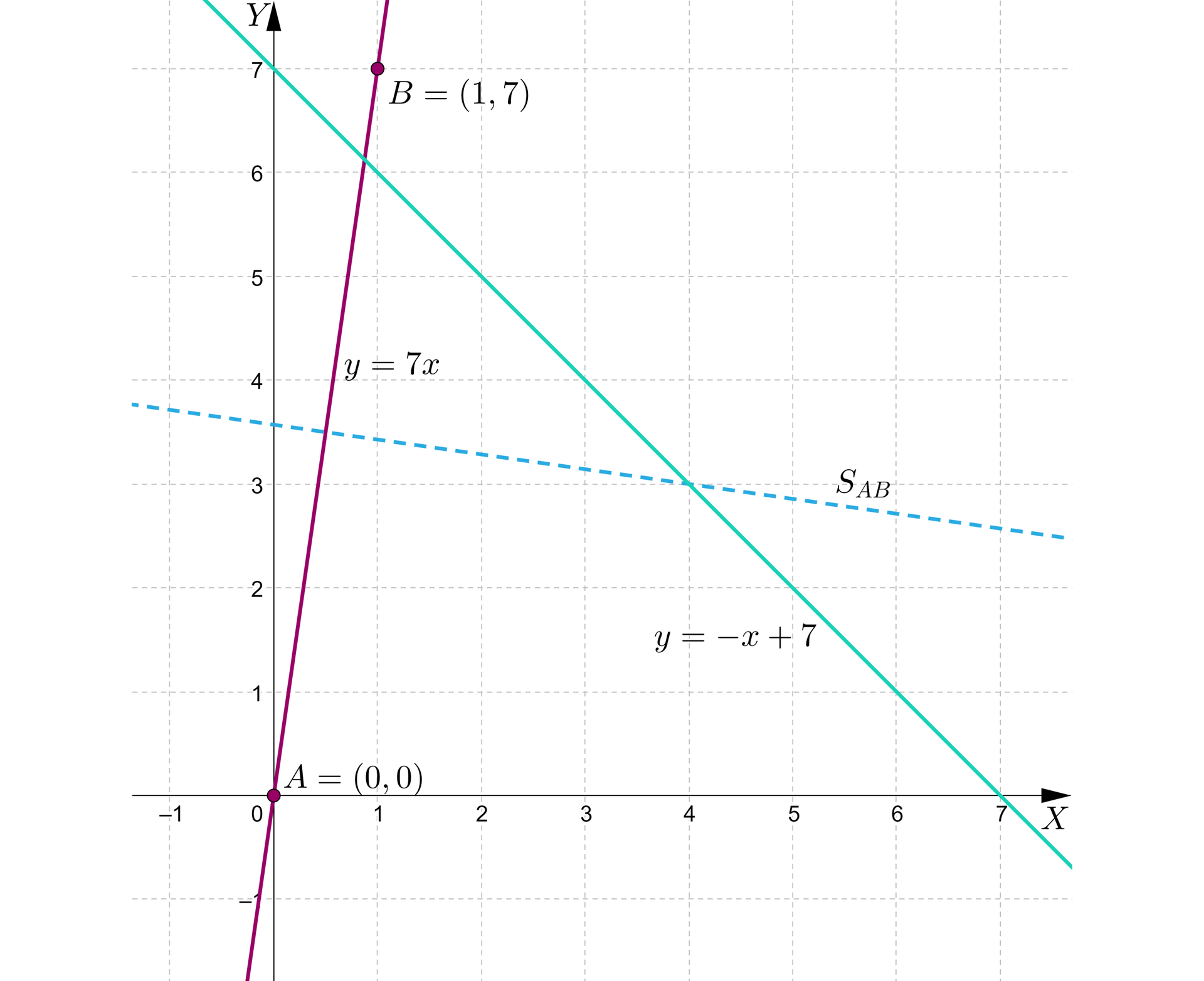
Rozpoczniemy od napisania równania symetralnej $S_{AB}$ odcinka $AB$.

Symetralna przechodzi przez środek odcinka $AB$ i jest do niego prostopadła. Wyznaczamy współrzędne środka odcinka $AB$. Ponieważ $A=\left(0,0\right)$ i $B=\left(1,7\right)$, to $\frac{x_A+x_B}{2}=\frac{0+1}{2}=\frac{1}{2}$ i $\frac{y_A+y_B}{2}=\frac{0+7}{2}=\frac{7}{2}$.

Współczynnik kierunkowy prostej przechodzącej przez punkty $A=\left(x_A,y_A\right)$ i $B=\left(x_B,y_B\right)$ obliczymy, podstawiając współrzędne punktów $A$ i $B$ do równania prostej $y=ax+b$.

$\left\{\begin{array}{l}{y}_A=a_{AB}·x_A+b\\ y_B=a_{AB}·x_B+b\end{array}\right.$

Odejmując od dolnego równania, równanie górne

$y_B-y_A=a_{AB}·x_B+b-a_{AB}·x_A+b$,

otrzymujemy

$a_{AB}=\frac{y_B-y_A}{x_B-x_A}$.

Obliczamy współczynnik kierunkowy prostej $AB$ z powyższego wzoru

$a_{AB}=\frac{y_B-y_A}{x_B-x_A}=\frac{7-0}{1-0}=7$.

Współczynnik kierunkowy prostej $AB$ jest równy $7$, więc z warunku prostopadłości prostych

$a_{S_{AB}}=-\frac{1}{a_{AB}}$

współczynnik kierunkowy prostej do niej prostopadłej jest równy $-\frac{1}{7}$.

Otrzymujemy $S_{AB}:y=-\frac{1}{7}x+b$.

Ponieważ prosta przechodzi przez punkt $\left(\frac{1}{2},\frac{7}{2}\right)$, to możemy obliczyć wyraz wolny $b$.

$\frac{7}{2}=-\frac{1}{7}·\frac{1}{2}+b$

$b=\frac{7}{2}+\frac{1}{14}$

$b=\frac{49}{14}+\frac{1}{14}$

$b=\frac{50}{14}=\frac{25}{7}$

Równanie symetralnej odcinka $AB$ ma postać

$y=-\frac{1}{7}x+\frac{25}{7}$.

Punkt wspólny prostych $y=-\frac{1}{7}x+\frac{25}{7}$ i $y=-x+7$ jest środkiem okręgu.

Rozwiązujemy układ równań.

$\left\{\begin{array}{l}y=-x+7\\ y=-\frac{1}{7}x+\frac{25}{7}\end{array}\right.$

$-x+7=-\frac{1}{7}x+\frac{25}{7}$

Mnożymy strony równania przez $7$ i wyznaczamy wartość $x$.

$-7x+49=-x+25$

$-6x=-24|:\left(-6\right)$

$x=4$

Ponieważ $y=-x+7$, to podstawiając obliczony $x_S=4$, $y_S=-4+7=3$

Zatem środek okręgu ma współrzędne $\left(4,3\right)$. Promień okręgu jest odległością środka okręgu od punktu leżącego na okręgu.

$r=\left|OA\right|=\sqrt{{\left(x_A-x_O\right)}^2+{\left(y_A-y_O\right)}^2}$

$r=\sqrt{4^2+3^2}=\sqrt{25}=5$

Szukane równanie okręgu jest postaci ${\left(x-4\right)}^2+{\left(y-3\right)}^2=5^2$.

okrąg o środku $O$ i promieniu $r$ to zbiór wszystkich punktów $P$ płaszczyzny, których odległość od punktu $O$ jest równa $r$

zbiór wszystkich punktów płaszczyzny równoodległych od końców tego odcinka