Rozwiążemy nierówność $\sin \left(x+\frac{\pi }{3}\right)·\cos 2x-\cos \left(x+\frac{\pi }{3}\right)·\sin 2x>0,5$.

Rozwiązanie

Skorzystamy ze wzoru na sinus różnicy argumentówsinus różnicy argumentówsinus różnicy argumentów, aby zwinąć wyrażenie znajdujące się po lewej stronie nierówności

$\sin \left(x+\frac{\pi }{3}-2x\right)>0,5$,

$\sin \left(\frac{\pi }{3}-x\right)>0,5$.

Przekształcamy nierówność do wygodniejszej postaci

$\sin \left(x-\frac{\pi }{3}\right)<-\frac{1}{2}$.

Odczytujemy rozwiązanie powyższej nierówności

$\left(x-\frac{\pi }{3}\right)\in \left(-\frac{5\pi }{6}+2k\pi ,-\frac{\pi }{6}+2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Ostatecznie rozwiązanie nierówności ma postać

$\left(-\frac{\pi }{2}+2k\pi ,\frac{\pi }{6}+2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Rozwiążemy nierówność $\sin \left(\frac{7\pi }{4}+x\right)+\sqrt{2}\cos \left(\frac{3\pi }{2}-x\right)\le 0$.

Rozwiązanie

Najpierw zauważmy, że możemy skorzystać ze wzoru na sinus sumy argumentówsinus sumy argumentówsinus sumy argumentów

$\sin \left(\frac{7\pi }{4}+x\right)=\sin \frac{7\pi }{4}·\cos x+\cos \frac{7\pi }{4}·\sin x$.

Podstawiamy do nierówności z zadania

$\sin \frac{7\pi }{4}·\cos x+\cos \frac{7\pi }{4}·\sin x-\sqrt{2}\sin x\le 0$.

Po podstawieniu wartości funkcji trygonometrycznych argumentów, otrzymujemy

$-\frac{\sqrt{2}}{2}\cos x+\frac{\sqrt{2}}{2}\sin x-\sqrt{2}\sin x\le 0$,

$-\frac{\sqrt{2}}{2}\cos x\le \frac{\sqrt{2}}{2}\sin x$.

Zatem nierówność z zadania jest równoważna następującej nierówności

$-\cos x\le \sin x$.

Najpierw rozwiążemy równanie

$-\cos x=\sin x$.

Ponieważ funkcje sinus i cosinus tego samego argumentu nie są jednocześnie równe $0$, możemy podzielić przez $\cos x$. Otrzymujemy wówczas

$tgx=-1$.

Rozwiązaniem tego równania są $x=-\frac{\pi }{4}+k\pi$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Rysujemy teraz wykresy funkcji $y=-\cos x$ oraz $y=\sin x$ i odczytujemy rozwiązanie nierówności.

RUwWBY9ATiMV5

Rysunek przedstawia układ współrzędnych z poziomą osią X od minus pi drugich do trzech drugich pi oraz z pionową osią Y od minus półtora do dwóch. Na płaszczyźnie narysowano wykres funkcji y równa się sinus x oraz y równa się minus cosinus x, która jest symetryczna do funkcji y równa się cosinus x względem osi X. Na osi X zaznaczono odcinek symbolizujący przedział domknięty. Odcinek ma końce w zamalowanych punktach $\left(-\frac{\pi }{4};0\right)$ i $\left(\frac{3\pi }{4};0\right)$. Z obu końców odcinków poprowadzono linią przerywaną pionowe odcinki do punktów przecięcia obu wykresów.

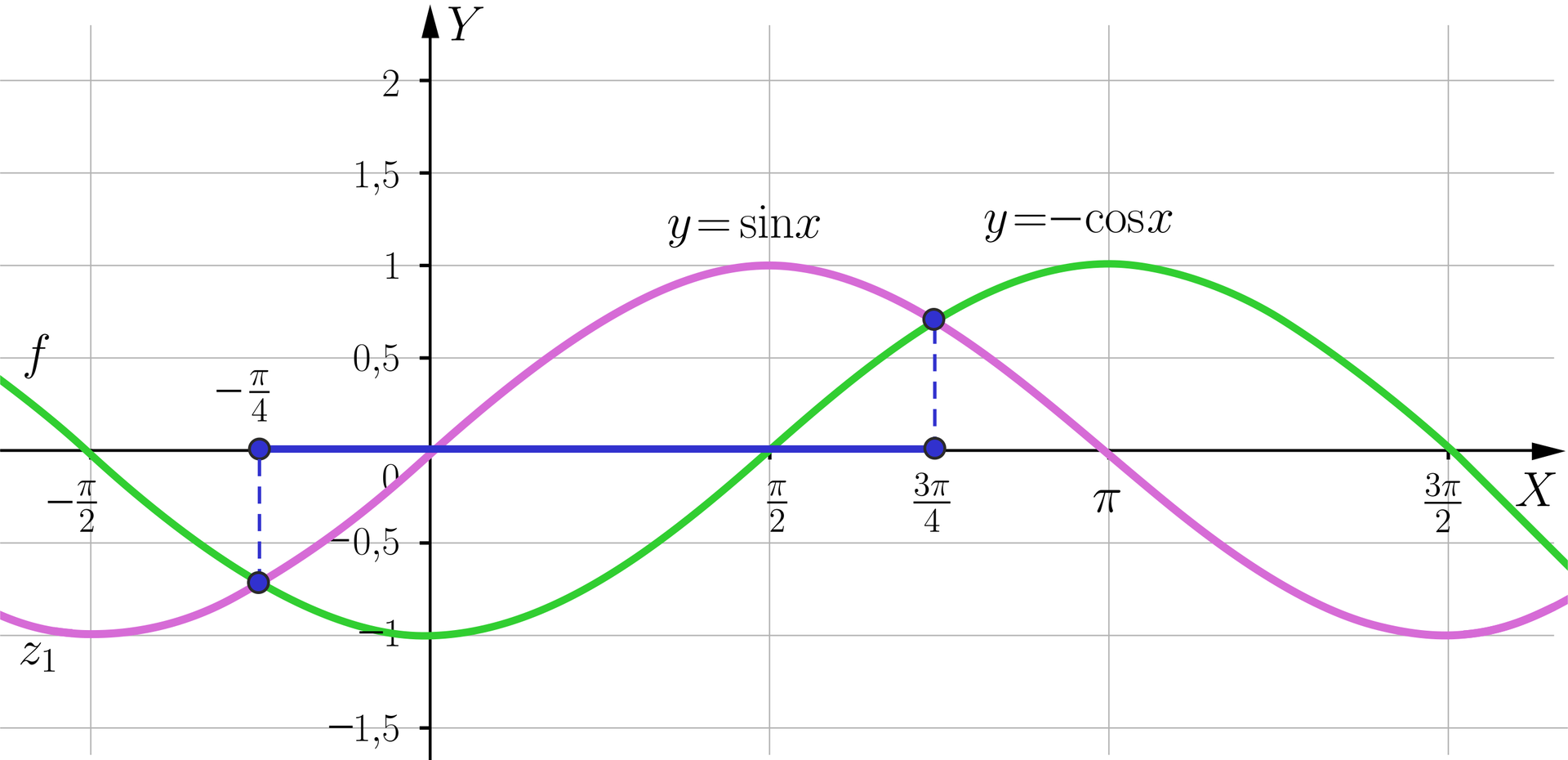
Ostatecznie rozwiązanie nierówności ma postać

$⟨-\frac{\pi }{4}+k\pi ,\frac{3\pi }{4}+k\pi ⟩$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Rozwiążemy nierówność $tg\left(\frac{\pi }{4}-x\right)>\frac{\cos x}{\sin x+\cos x}$.

Rozwiązanie

Korzystamy ze wzoru na tangens różnicy argumentówtangens różnicy argumentówtangens różnicy argumentów

$\frac{tg\frac{\pi }{4}-tgx}{1+tg\frac{\pi }{4}·tgx}>\frac{\cos x}{\sin x+\cos x}$.

Otrzymujemy zatem

$\frac{1-tgx}{1+tgx}-\frac{\cos x}{\sin x+\cos x}>0$.

Zwróćmy uwagę na ważną i interesującą, szczególną zależność

$tg\left(\frac{\pi }{4}-x\right)=\frac{1-tgx}{1+tgx}$.

Dokonajmy przekształcenia wyrażenia zawierającego wartości funkcji tangens na wyrażenie zawierające tylko wartości funkcji sinus i cosinus

$\frac{1-tgx}{1+tgx}=\frac{\frac{\cos x-\sin x}{\cos x}}{\frac{\cos x+\sin x}{\cos x}}=\frac{\cos x-\sin x}{\cos x+\sin x}$.

Zatem nierówność przyjmuje postać

$\frac{\cos x-\sin x}{\cos x+\sin x}>\frac{\cos x}{\cos x+\sin x}$.

A stąd mamy

$\frac{\sin x}{\cos x+\sin x}<0$.

Korzystając ze wzoru na sinus sumy argumentów, zwiniemy mianownik lewej strony nierówności do postaci jednej funkcji trygonometrycznej

$\cos x+\sin x=\sqrt{2}\left(\frac{1}{\sqrt{2}}\cos x+\frac{1}{\sqrt{2}}\sin x\right)=$

$=\sqrt{2}\left(\sin \frac{\pi }{4}·\cos x+\cos \frac{\pi }{4}·\sin x\right)=\sqrt{2}\sin \left(\frac{\pi }{4}+x\right)$.

Zatem nierówność

$\sin x\left(\cos x+\sin x\right)<0$

możemy zapisać w postaci równoważnej

$\sqrt{2}\sin \left(\frac{\pi }{4}+x\right)\sin x<0$,

czyli

$\sin \left(\frac{\pi }{4}+x\right)\sin x<0$.

Nierówność jest równoważna alternatywie warunków:

($\sin x<0$ i $\sin \left(\frac{\pi }{4}+x\right)<0$) lub ($\sin x>0$ i $\sin \left(\frac{\pi }{4}+x\right)>0$).

Rozważmy dwa przypadki.

Przypadek 1

Niech $\sin x<0$ i  $\sin \left(\frac{\pi }{4}+x\right)<0$.

Nierówność $\sin x<0$ zachodzi dla $x\in (-\pi +2k\pi ,2k\pi )$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Nierówność $\sin \left(\frac{\pi }{4}+x\right)<0$ zachodzi dla

$\left(\frac{\pi }{4}+x\right)\in \left(-\pi +2k\pi ,2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$, czyli

$x\in \left(-\frac{5\pi }{4}+2k\pi ,-\frac{\pi }{4}+2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Ostatecznie w przypadku pierwszym rozwiązaniem jest zbiór

$x\in \left(-\pi +2k\pi ,-\frac{\pi }{4}+2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Przypadek 2

Niech $\sin x>0$ i $\sin \left(\frac{\pi }{4}+x\right)>0$.

Nierówność $\sin x>0$ jest spełniona dla

$x\in \left(2k\pi ,\pi +2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Nierówność $\sin \left(\frac{\pi }{4}+x\right)>0$ jest spełniona dla

$\left(\frac{\pi }{4}+x\right)\in \left(2k\pi ,\pi +2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$, czyli

$x\in \left(-\frac{\pi }{4}+2k\pi ,\frac{3\pi }{4}+2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Ostatecznie w przypadku drugim rozwiązaniem jest zbiór

$\left(2k\pi ,\frac{3\pi }{4}+2k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Po zsumowaniu zbiorów z obu przypadków otrzymujemy

$x\in \left(k\pi ,\frac{3\pi }{4}+k\pi \right)$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Rozwiążemy nierówność $\left(\sqrt{6}+\sqrt{2}\right)\cos x-\left(\sqrt{6}-\sqrt{2}\right)\sin x\ge 2$.

Rozwiązanie

Aby rozwiązać to zadanie, skorzystamy z zależności:

$\cos \frac{\pi }{12}=\frac{\sqrt{6}+\sqrt{2}}{4}$ i $\sin \frac{\pi }{12}=\frac{\sqrt{6}-\sqrt{2}}{4}$.

Dzielimy nierówność stronami przez $4$

$\frac{\sqrt{6}+\sqrt{2}}{4}\cos x-\frac{\sqrt{6}-\sqrt{2}}{4}\sin x\ge \frac{1}{2}$.

Podstawiamy funkcje trygonometryczne argumentu $\frac{\pi }{12}$

$\cos \frac{\pi }{12}\cos x-\sin \frac{\pi }{12}\sin x\ge \frac{1}{2}$.

Korzystamy ze wzoru na cosinus sumy argumentówcosinus sumy argumentówcosinus sumy argumentów

$\cos \left(\frac{\pi }{12}+x\right)\ge \frac{1}{2}$.

Rozwiązujemy nierówność

$\left(\frac{\pi }{12}+x\right)\in ⟨-\frac{\pi }{3}+2k\pi ,\frac{\pi }{3}+2k\pi ⟩$, gdzie $k\in \mathrm{\mathbb{Z}}$.

Zatem rozwiązaniem nierówności z zadania jest zbiór

$⟨-\frac{5\pi }{12}+2k\pi ,\frac{\pi }{4}+2k\pi ⟩$, gdzie $k\in \mathrm{\mathbb{Z}}$.

$\sin \left(x+y\right)=\sin x·\cos y+\cos x·\sin y$, dla $x,y\in \mathrm{ℝ}$

$\sin \left(x-y\right)=\sin x·\cos y-\cos x·\sin y$, dla $x,y\in \mathrm{ℝ}$

$\cos \left(x+y\right)=\cos x·\cos y-\sin x·\sin y$, dla $x,y\in \mathrm{ℝ}$

$\mathrm{tg}\left(x-y\right)=\frac{\mathrm{tg}x-\mathrm{tg}y}{1+\mathrm{tg}x\mathrm{tg}y}$,

gdy $x\ne \frac{\pi }{2}+k\pi$, $y\ne \frac{\pi }{2}+k\pi$, $x-y\ne \frac{\pi }{2}+k\pi$, gdzie $k\in \mathrm{\mathbb{Z}}$