Przeczytaj

Ciąg liczbowy

Definicja: Ciąg liczbowy

Ciąg, w którym wyrazy są liczbami, nazywamy ciągiem liczbowym.

Jednym ze sposobów określania ciągu liczbowego jest podanie wzoru na $n$ –ty wyraz ciągu. Wzór ten nazywamy wyrazem ogólnym ciągu.

W wielu wypadkach wzór ogólny ciągu można ustalić, na podstawie kilku wyrazów początkowych tego ciągu.

Przykład 1

Kolejne wyrazy ciągu $(a_{n})$	Wzór ogólny ciągu
$1$ , $3$ , $5$ , $7$ , $9$ ,...	$a_{n} = 2 n - 1$
$- 1$ , $3$ , $- 1$ , $3$ , $- 1$ , $3$ , ...	$a_{n} = {(- 1)}^{n} \cdot 2 + 1$
$6$ , $12$ , $20$ , $30$ , $42$ ,...	$a_{n} = (n + 1) (n + 2)$

Przykład 2

R14HJI9h71PVZ

Rysunek przedstawia kolejne wyrazy ciągu zilustrowane kostkami składającymi się z małych sześcianów. Każda kostka składa się z odpowiedniej liczby sześcianów równej wielkości danego wyrazu ciągu. Wyrazy ciągu: 20=1 kostka składa się z jednego sześcianu, 21=2 kostka składa się z dwóch sześcianów, 22=4 kostka składa się z czterech sześcianów, 23=8 kostka składa się z ośmiu sześcianów, 24=16 kostka składa się z szesnastu sześcianów, 25=32 kostka składa się z trzydziestu dwóch sześcianów, 26=64 kostka składa się z sześćdziesięciu czterech sześcianów, 27=128 kostka składa się z stu dwudziestu ośmiu sześcianów, 28=256 kostka składa się z dwustu pięćdziesięciu sześciu sześcianów, 29=512 kostka składa się z pięciuset dwunastu sześcianów, 210=1024 kostka składa się z tysiąca dwudziestu czterech sześcianów.

Liczba dwa jest podstawą binarnego systemu liczenia. Ciąg kolejnych naturalnych potęg liczby dwa $(d_{n})$ ma więc duże znaczenie w informatyce. Zapisane w systemie dwójkowym potęgi liczby $2$ składają się tylko z zer i jedynki:

1

10

100

1000

10000

, ...

W systemie dziesiętnym kolejne wyrazy ciągu $(d_{n})$ to:

1

2

4

8

16

32

64

, ...

Wyraz ogólny ciągu $(d_{n})$ dany jest zatem wzorem:

d_{n} = 2^{n}

gdzie $n \in ℕ$ .

Przykład 3

Liczby Mersenne’a to liczby postaci $M_{n} = 2^{n} - 1$ , gdzie $n$ jest liczbą naturalną. Liczby Mersenne’a zostały tak nazwane na cześć siedemnastowiecznego francuskiego matematyka Marina Mersenne’a, który uważał, że za pomocą tego wzoru można znaleźć dowolną liczbę pierwszą.

Niestety, pomylił się.

Liczby Mersenne’a są liczbami pierwszymi, gdy $n$ jest liczbą pierwszą (ale nie dowolną!). Nie wiadomo, czy ciąg $(M_{n})$ , utworzony z takich liczb jest nieskończony.

Początkowe kolejne liczby pierwsze ciągu $(M_{n})$ .

$n$	$M_{n}$
$2$	$3$
$3$	$7$
$5$	$31$
$7$	$127$
$13$	$8191$
$17$	$131071$

Przykład 4

Liczby Catalana to ciąg liczbowyciąg liczbowyciąg liczbowy, nazwany tak na cześć dziewiętnastowiecznego belgijskiego matematyka Charlesa Catalana.

Liczby te określone są wzorem:

C_{n} = \frac{1}{n + 1} \cdot (\begin{matrix} 2 n \\ n \end{matrix})

dla

n \geq 0

Kolejne liczby Catalana to:

1

1

2

5

14

42

132

, ...

Liczby Catalana mają duże znaczenie w krystalografii, logistyce, kombinatoryce.

Za pomocą liczb Catalana można określić na przykład liczbę możliwych dróg prowadzących po krawędziach kraty w prawo w górę z lewego dolnego do prawego górnego rogu.

Poniższe wykresy pokazują przypadek dla $n = 4$ : $C_{4} = 14$ .

R1Wpbbb8xUvjH

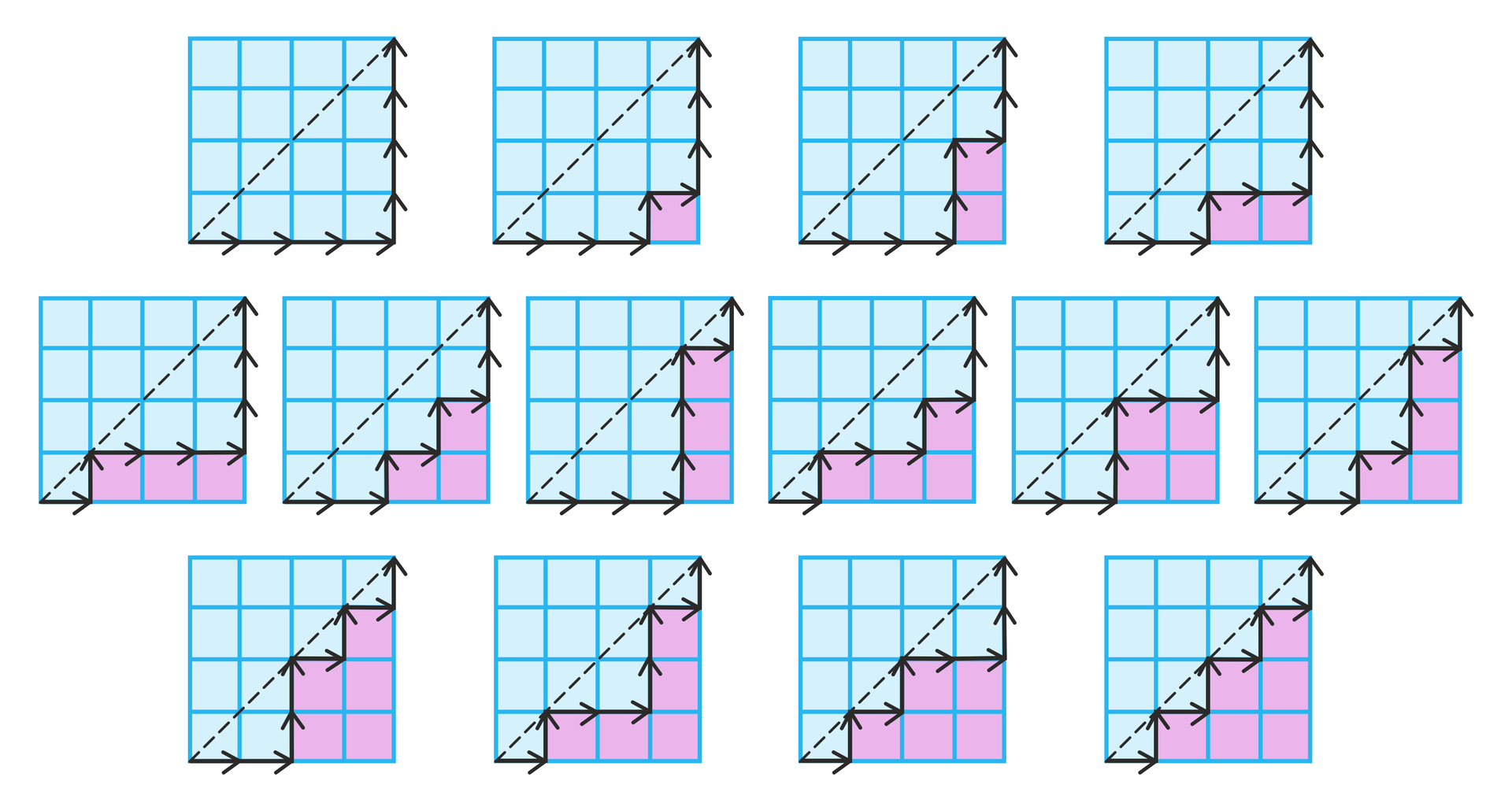
Ilustracja przedstawia czternaście kwadratów ustawionych w trzech rzędach: w pierwszym rzędzie 4 kwadraty, w drugim 6, a w trzecim rzędzie znajdują się 4 kwadraty. Każdy kwadrat podzielony jest na szesnaście mniejszych kwadratów. W każdym dużym kwadracie narysowano linią przerywaną przekątną biegnącą od lewego dolnego do prawego górnego wierzchołka figury. Na każdym dużym kwadracie strzałkami zaznaczono drogę, jaką można dostać się z dolnego lewego wierzchołka do górnego prawego. Każda strzałka jest długości boku małego kwadratu. Strzałki biegną tylko wzdłuż boków małych kwadratów, więc są tylko pionowe lub poziome, a ich groty skierowane są tylko w prawo (w poziomych strzałkach) lub w górę (w pionowych strzałkach). Każda droga pokazana na figurach ma ten sam początek (lewy dolny wierzchołek) i koniec (prawy górny wierzchołek). Kwadrat pierwszy. Cztery strzałki biegną wzdłuż podstawy dużego kwadratu, cztery kolejne biegną w górę wzdłuż prawego boku kwadratu. Kwadrat drugi. Trzy strzałki biegną poziomo wzdłuż podstawy kwadratu, jedna w górę, jedna w prawo, trzy w górę wzdłuż prawego boku figury. Tutaj strzałki podzieliły pole kwadratu na dwie części, wyodrębniając kwadracik leżący przy prawym dolnym wierzchołku. Kwadracik wyróżniono kolorem. Trzeci kwadrat. Trzy strzałki biegną poziomo wzdłuż podstawy figury, dwie biegną w górę, jedna w prawo, dwie w górę wzdłuż prawego boku figury. Kolorem wyróżniono dwa wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku i jeden nad nim. Czwarty kwadrat. Dwie strzałki biegną poziomo wzdłuż podstawy figury, jedna biegnie w górę, dwie w prawo, trzy w górę wzdłuż prawego boku figury. Kolorem wyróżniono dwa wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku i jeden po jego lewej stronie. Piąty kwadrat. Jedna strzałka biegnie poziomo wzdłuż podstawy figury, jedna biegnie w górę, trzy w prawo, trzy w górę wzdłuż prawego boku figury. Kolorem wyróżniono trzy wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku i dwa po jego lewej stronie. Szósty kwadrat. Dwie strzałki biegną poziomo wzdłuż podstawy figury, jedna biegnie w górę, jedna w prawo, jedna w górę, jedna w prawo, dwie wzdłuż prawego boku figury. Kolorem wyróżniono trzy wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku, jeden nad nim i jeden po jego lewej stronie. Siódmy kwadrat. Trzy strzałki biegną poziomo wzdłuż podstawy figury, trzy biegną w górę, jedna w prawo, jedna w górę wzdłuż prawego boku figury. Kolorem wyróżniono trzy wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku i dwa nad nim. Ósmy kwadrat. Jedna strzałka biegnie poziomo wzdłuż podstawy figury, jedna biegnie w górę, dwie w prawo, jedna w górę, jedna w prawo, dwie wzdłuż prawego boku figury. Kolorem wyróżniono cztery wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku, jeden nad nim i dwa po jego lewej stronie. Dziewiąty kwadrat. Dwie strzałki biegną poziomo wzdłuż podstawy figury, dwie biegną w górę, dwie w prawo, dwie w górę wzdłuż prawego boku figury. Kolorem wyróżniono cztery wyodrębnione strzałkami kwadraciki, które składają się na ćwiartkę dużej figury leżącą w jej prawej dolnej części. Dziesiąty kwadrat. Dwie strzałki biegną poziomo wzdłuż podstawy figury, jedna biegnie w górę, jedna w prawo, dwie w górę, jedna w prawo, jedna w górę wzdłuż prawego boku figury. Kolorem wyróżniono cztery wyodrębnione strzałkami kwadraciki – jeden znajdujący się przy prawym dolnym wierzchołku, dwa nad nim i jeden po jego lewej stronie. Jedenasty kwadrat. Dwie strzałki biegną poziomo wzdłuż podstawy figury, dwie biegną w górę, jedna w prawo, jedna w górę, jedna w prawo, jedna wzdłuż prawego boku figury. Kolorem wyróżniono pięć wyodrębnionych strzałkami kwadracików – jeden znajdujący się przy prawym dolnym wierzchołku, dwa nad nim, jeden po jego lewej stronie i jeden nad tym kwadracikiem. Dwunasty kwadrat. Jedna strzałka biegnie poziomo wzdłuż podstawy figury, jedna biegnie w górę, dwie w prawo, dwie w górę, jedna w prawo, jedna w górę wzdłuż prawego boku figury. Kolorem wyróżniono pięć wyodrębnionych strzałkami kwadracików – jeden znajdujący się przy prawym dolnym wierzchołku, dwa nad nim i dwa po jego lewej stronie. Trzynasty kwadrat. Jedna strzałka biegnie poziomo wzdłuż podstawy figury, jedna biegnie w górę, jedna w prawo, jedna w górę, dwie w prawo, dwie w górę wzdłuż prawego boku figury. Kolorem wyróżniono pięć wyodrębnionych strzałkami kwadracików – cztery składające się się na ćwiartkę pola kwadratu leżącą w prawej dolnej części oraz jeden znajdujący się po lewo od ćwiartki, przy podstawie figury. Czternasty kwadrat. Jedna strzałka biegną poziomo wzdłuż podstawy figury, jedna biegnie w górę, jedna w prawo, jedna w górę, jedna w prawo, jedna w górę, jedna w prawo, jedna w górę wzdłuż prawego boku figury. Kolorem wyróżniono sześć wyodrębnionych strzałkami kwadracików, czyli znajdującą się w dolnej prawej części ćwiartkę pola oraz jeden kwadracik po jej lewej stronie leżący przy podstawie figury i jeden kwadracik leżący nad ćwiartką leżący przy prawym boku figury.

Przykład 5

Liczby Fermata to liczby naturalne postaci:

F_{n} = 2^{2^{n}} + 1

dla

n \geq 0 .

Liczby te zostały tak nazwane na cześć francuskiego siedemnastowiecznego matematyka Pierra Fermata.

Kilka początkowych liczb tworzących ciąg Fermata:

3

5

17

257

65537

, ...

Początkowe liczby Fermata to liczby pierwsze. Fermat uważał, że wszystkie liczby postaci $2^{2^{n}} + 1$ są pierwsze. Jednak okazało się, że już $F_{5}$ jest liczbą złożoną.

Przykład 6

Liczby, będące sumą elementów, z których zbudowane są sześcioramienne gwiazdy, wykonane na kształt chińskich warcabów, tworzą ciąg $(g_{n})$ , zwany ciągiem liczb gwiazd.

R1DRFhMdIZgZR

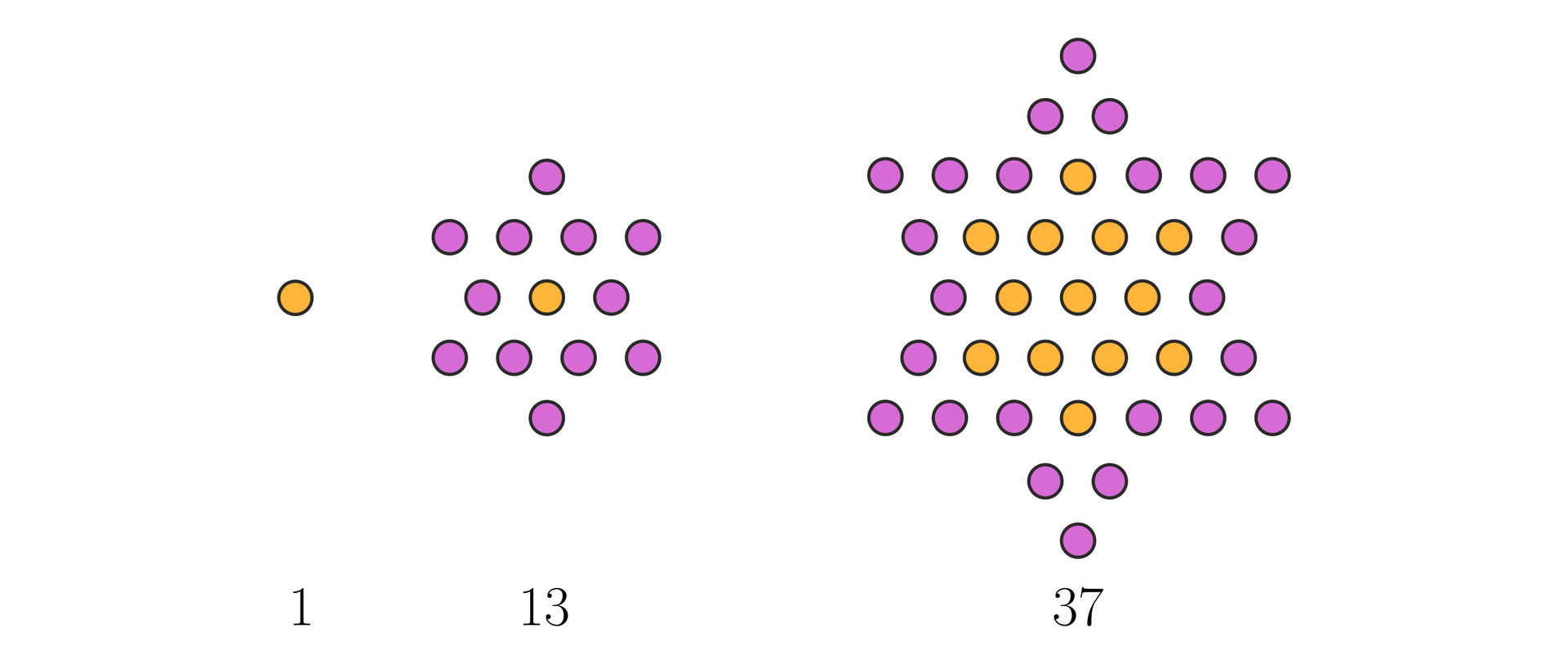
Ilustracja przedstawia trzy rysunki obok siebie. Rysunek pierwszy to pomarańczowe małe koło podpisane cyfrą jeden. Druga ilustracja to sześcioramienna gwiazda składająca się z trzynastu kół – koło środkowe jest pomarańczowe, pozostałe są fioletowe. Rysunek podpisano liczbą trzynaście. Trzeci rysunek to sześcioramienna gwiazda składająca się z trzydziestu siedmiu kół – wewnętrzne koła są pomarańczowe – jest ich trzynaście. Zewnętrzne koła tworzą kontur gwiazdy i są zamalowane kolorem fioletowym. Rysunek podpisano liczbą trzydzieści siedem.

Ciąg $(g_{n})$ określony jest wzorem:

g_{n} = 6 n (n - 1) + 1

Kilka początkowych wyrazów ciągu:

1

13

37

73

121

181

253

337

433

, ...

Przykład 7

Liczby Cullena to liczby postaci $C_{n} = n \cdot 2^{n} + 1$ dla $n \geq 1$ . Liczby te jako pierwsze badał dziewiętnastowieczny irlandzki matematyk James Cullen. Udowodniono, że w ciągu, którego kolejnymi wyrazami są liczby Cullena, liczb złożonych Cullena jest nieskończenie wiele, natomiast liczb Cullena pierwszych nie wiadomo, czy jest nieskończenie wiele.

Przykład 8

Liczby prostokątne, to liczby, którymi zajmowali się uczeni już w czasach Arystotelesa. Są to liczby będące iloczynem dwóch kolejnych liczb naturalnych. Są one kolejnymi wyrazami ciągu $(p_{n})$ :

2

6

12

20

30

42

56

, ...

R6mY6rBbhYy6D

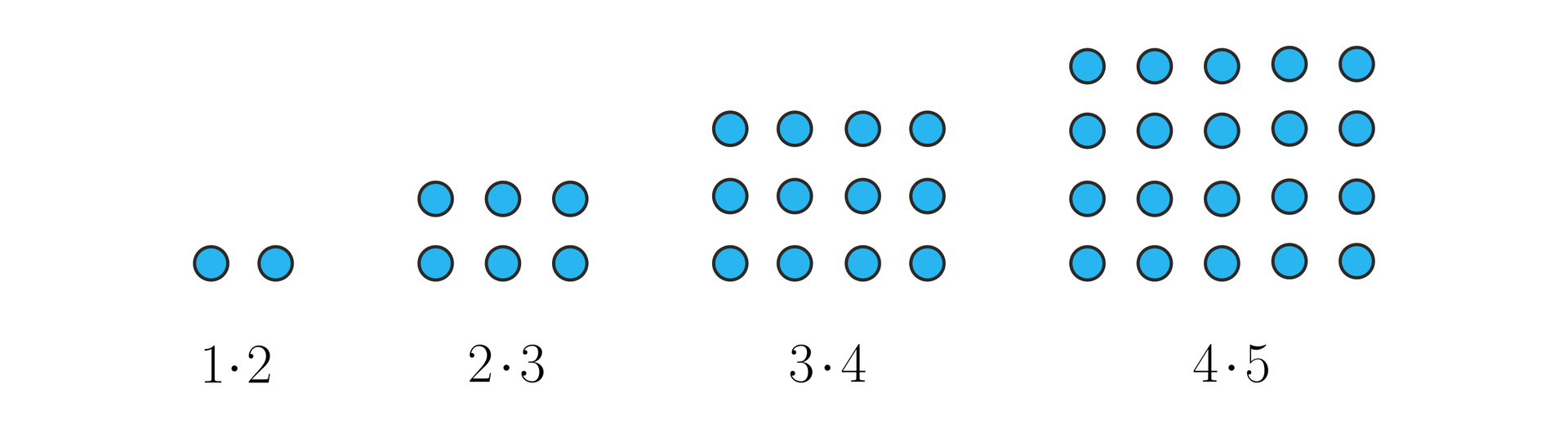
Ilustracja składa się z czterech rysunków, na których znajdują się koła układające się w prostokąty. Rysunek pierwszy to dwa ułożone obok siebie koła, podpisane jako 1 razy dwa. Rysunek drugi to sześć kół ułożonych w dwóch rzędach po trzy. Podpis: 2 razy trzy. Rysunek trzeci to 12 kół ułożonych w trzech rzędach po cztery. Podpis: 3 razy cztery. Rysunek czwarty to 20 kół ułożonych w czterech rzędach po pięć. Podpis: 4 razy pięć.

Nieskończona suma odwrotności liczb prostokątnych jest równa $1$ .

\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \dots = 1

Suma początkowych $n$ tych liczb wyraża się wzorem:

S_{n} = \frac{n}{n + 1}

Przykład 9

Liczby Carmichaela to liczby, których nazwa pochodzi od nazwiska Roberta Carmichaela, który określił je w $1910 r.$

Liczba naturalna jest liczbą Carmichaela wtedy i tylko wtedy, gdy:

jest liczbą złożoną,
dla każdej liczby naturalnej $k$ takiej, że $1 < k < n$ , względnie pierwszej z liczbą naturalną $n$ , liczba $(k^{n - 1} - 1)$ jest podzielna przez $n$ .

Udowodniono, że liczb Carmichaela jest nieskończenie wiele.

Wyraz ogólny ciągu $(M_{n})$ , którego wyrazami są kolejne liczby Carmichaela o trzech czynnikach pierwszych, wyraża się wzorem:

M_{n} = (6 m + 1) (12 m + 1) (18 m + 1)

Jeśli dla $m$ wszystkie czynniki są liczbami pierwszymi to $M_{n}$ jest liczbą Carmichaela.

Przykłady liczb Carmichaela.

5 \cdot 13 \cdot 17 = 1105

7 \cdot 13 \cdot 19 = 1729

5 \cdot 17 \cdot 29 = 2465

7 \cdot 13 \cdot 31 = 2821

Słownik

ciąg liczbowy

ciąg, w którym wyrazy są liczbami

Wprowadzenie

Animacja

Słownik