Przeczytaj

Już wiesz

Funkcją logarytmicznąfunkcja logarytmicznaFunkcją logarytmiczną nazywamy funkcję postaci $f (x) = \log_{a} x$ , gdzie $x > 0$ oraz $a > 0$ i $a \neq 1$ .

Wykresem funkcji logarytmicznejfunkcja logarytmicznafunkcji logarytmicznej jest krzywa logarytmiczna.

W trakcie lekcji omówimy własności wykresu funkcji logarytmicznej dla $a \in (0, 1)$ .

Na rysunkach przedstawiono wykres funkcji logarytmicznych określonych wzorami $f (x) = \log_{\frac{1}{2}} x$ oraz $g (x) = \log_{\frac{1}{3}} x$ .

Tabele wartości tych funkcji przedstawiają się następująco:

$x$	$\frac{1}{4}$	$\frac{1}{2}$	$1$	$2$
$f (x)$	$2$	$1$	$0$	$- 1$

$x$	$\frac{1}{9}$	$\frac{1}{3}$	$1$	$3$
$g (x)$	$2$	$1$	$0$	$- 1$

R1d7vrvIDBN7g

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do sześciu oraz z pionową osią Y od minus trzech do pięciu. Na płaszczyźnie zaznaczono wykres funkcji logarytmicznej f o podstawie równej 12. Wykres tej funkcji leży w pierwszej i czwartej ćwiartce i jest symetryczny względem osi X do wykresu funkcji logarytmicznej zadanej wzorem y=log2x. Funkcja ta jest malejąca, jej asymptotą pionową jest oś Y. Wykres funkcji f przechodzi przez punkty: 1,0 oraz 2,-1, z czego punkt przecięcia wykresu z osią X wyróżniono.

RXjqbVOIc7rgF

Na podstawie wykresu funkcji określonej wzorem $f (x) = \log_{a} x$ dla $a \in (0, 1)$ możemy odczytać następujące własności:

asymptotą wykresu funkcji jest prosta $x = 0$ ,
wykres funkcji zawsze przechodzi przez punkt $(1, 0)$ , bo $\log_{a} 1 = 0$ ,
wykres funkcji znajduje się w $I$ i $IV$ ćwiartce układu współrzędnych, bo funkcja jest określona tylko dla $x > 0$ ,
z wykresu odczytujemy, że zachodzą własności $f (x) > 0$ dla $x \in (0, 1)$ oraz $f (x) < 0$ dla $x \in (1, \infty)$ .

Mając dany punkt, który należy do wykresu funkcji logarytmicznej, możemy wyznaczyć jej wzór.

Przykład 1

Na rysunku przedstawiono wykres funkcji określonej wzorem $f (x) = \log_{a} x$ . Wyznaczymy wzór tej funkcji.

RQyJW6Rw3H8fR

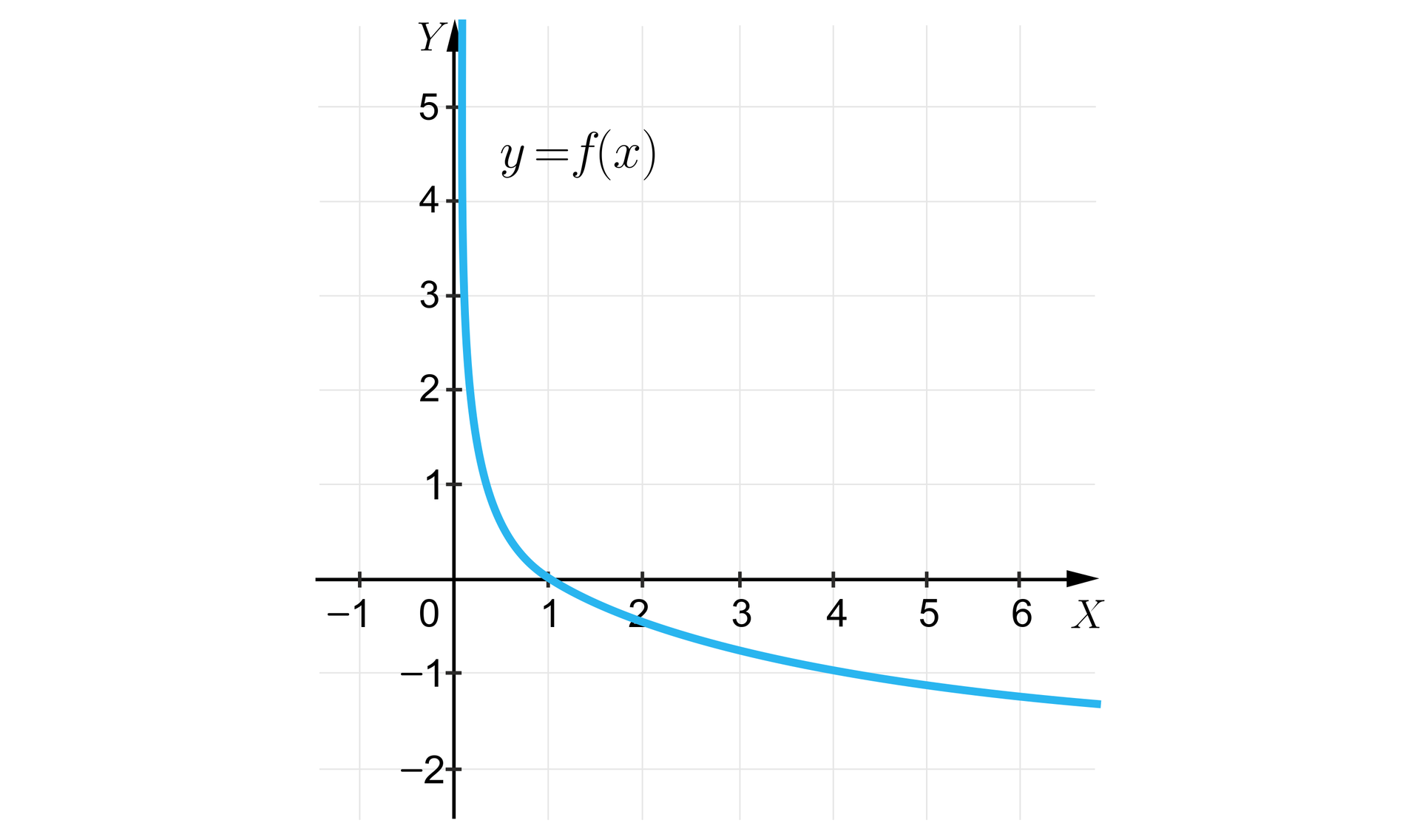
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do sześciu oraz z pionową osią Y od minus dwóch do pięciu. Na płaszczyźnie zaznaczono wykres funkcji logarytmicznej f o podstawie mniejszej od jeden. Wykres tej funkcji leży w pierwszej i w czwartej ćwiartce. Funkcja ta jest malejąca, jej asymptotą pionową jest oś Y. Wykres funkcji f przechodzi przez punkty: 1,0 oraz 4,-1, z czego punkt przecięcia wykresu z osią X wyróżniono.

Z wykresu możemy odczytać, że należy do niego punkt o współrzędnych $(4, - 1)$ .

Po podstawieniu do wzoru funkcji $f (x) = \log_{a} x$ współrzędnych punktu $(4, - 1)$ otrzymujemy równanie $- 1 = \log_{a} 4$ , co jest równoważne równaniu $a^{- 1} = 4$ .

Zatem $a = \frac{1}{4}$ , więc funkcja jest określona za pomocą wzoru $f (x) = \log_{\frac{1}{4}} x$ .

Przykład 2

Do wykresu funkcji określonej wzorem $f (x) = \log_{a} x$ należy punkt o współrzędnych $(8, - 3)$ . Wyznaczymy wzór tej funkcji.

Wiadomo, że $a \in (0, 1) \cup (1, \infty)$ .

Po podstawieniu do wzoru funkcji $f (x) = \log_{a} x$ współrzędnych punktu $(8, - 3)$ otrzymujemy równanie: $- 3 = \log_{a} 8$ , co jest równoważne równaniu $a^{- 3} = 8$ .

Z powyższego równania mamy, że $a = 8^{- \frac{1}{3}}$ , czyli $a = \frac{1}{2}$ .

Zatem funkcję określamy za pomocą wzoru $f (x) = \log_{\frac{1}{2}} x$ .

Przykład 3

Wiedząc, że miejscem zerowym funkcji logarytmicznej określonej wzorem $f (x) = \log_{\frac{1}{2}} (2 a^{2} x)$ jest liczba $1$ , wyznaczymy wartość parametru a.

Jeżeli $1$ jest miejscem zerowym podanej funkcji, to $0 = \log_{\frac{1}{2}} (2 a^{2})$ .

Równość tą można zapisać w postaci:

$2 a^{2} = {(\frac{1}{2})}^{0}$ .

Zatem $a^{2} = \frac{1}{2}$ , więc $a = \frac{\sqrt{2}}{2}$ lub $a = - \frac{\sqrt{2}}{2}$ .

Niezależnie od wyboru wartości współczynnika $a$ przy warunku, że $x > 0$ liczba logarytmowana $2 a^{2} x > 0$ , bo iloczyn liczby dodatniej i podwojonego kwadratu liczby różnej od $0$ jest dodatni.

Przykład 4

Do wykresu funkcji logarytmicznej określonej wzorem $f (x) = \log_{\frac{1}{3}} (p x + q)$ należą punkty o współrzędnych $(3, - 2)$ oraz $(2, - 3)$ . Wyznaczymy wartości parametrów $p$ i $q$ .

Współrzędne punktów podstawiamy do wzoru funkcji. Otrzymujemy układ równań:

$\{\begin{cases} - 2 = \log_{\frac{1}{3}} (3 p + q) \\ - 3 = \log_{\frac{1}{3}} (2 p + q) \end{cases}$

Układ równań sprowadzamy do postaci: $\{\begin{cases} 3 p + q = 9 \\ 2 p + q = 27 \end{cases}$

Zatem wartości parametrów $p$ i $q$ wynoszą odpowiednio: $p = - 18$ oraz $q = 63$ .

Sprawdzenie:

$- 2 = \log_{\frac{1}{3}} (- 18 \cdot 3 + 63)$ , więc $- 2 = \log_{\frac{1}{3}} 9$ ,

$- 3 = \log_{\frac{1}{3}} (- 18 \cdot 2 + 63)$ , więc $- 3 = \log_{\frac{1}{3}} 27$ .

Ważne!

Z faktu, że funkcja logarytmiczna określona wzorem $f (x) = \log_{a} x$ , gdzie $a \in (0, 1)$ jest malejąca wynika poniższa własność.

Dla dowolnych $x, y \in D_{f}$ mamy:

$\log_{a} x < \log_{a} y \Leftrightarrow x > y$ .

Korzystając z powyższej własności możemy znajdować rozwiązania nierówności, w których występują funkcje logarytmiczne.

Przykład 5

Wyznaczymy wartości $x$ , dla których zachodzi nierówność $\log_{\frac{1}{2}} (x - 2) < \log_{\frac{1}{2}} (2 x - 4)$ .

W celu ustalenia dziedziny logarytmu rozwiązujemy nierówności $x - 2 > 0$ i $2 x - 4 > 0$ , zatem $x \in (2, \infty)$ .

Z faktu, że funkcja wykładniczamonotoniczność funkcji logarytmicznejfunkcja wykładnicza dla $a \in (0, 1)$ jest malejąca wynika, że $x - 2 > 2 x - 4$ , zatem $x \in (- \infty, 2)$ .

Częścią wspólną przedziału określającego dziedzinę oraz rozwiązania nierówności jest zbiór pusty.

Zatem nie istnieje taki $x$ .

Wykorzystując własności wykresu funkcji logarytmicznej możemy wyznaczyć argumenty, dla których funkcja przyjmuje wartości dodatnie lub ujemne.

Przykład 6

Wyznaczymy, dla jakich argumentów funkcja zadana wzorem $f (x) = \log_{\frac{1}{2}} (x - 3)$ przyjmuje wartości ujemne.

W celu ustalenia dziedziny logarytmu rozwiązujemy nierówność $x - 3 > 0$ , zatem $x \in (3, \infty)$ .

Jeżeli $f (x) < 0$ , to $x - 3 > 1$ , zatem $x \in (4, \infty)$ .

Szukamy część wspólną rozwiązania i dziedziny.

Otrzymujemy, że $x \in (4, \infty)$ .

Przykład 7

Wyznaczymy, dla jakich argumentów funkcja określona wzorem $f (x) = \log_{\frac{1}{4}} (2 x - 1)$ przyjmuje wartości dodatnie.

W celu ustalenia dziedziny logarytmu rozwiązujemy nierówność $2 x - 1 > 0$ , więc $x \in (\frac{1}{2}, \infty)$ .

Jeżeli $f (x) > 0$ , to $0 < 2 x - 1 < 1$ , więc $x \in (\frac{1}{2}, 1)$ .

Funkcja przyjmuje wartości dodatnie dla argumentów $x \in (\frac{1}{2}, 1)$ .

Słownik

funkcja logarytmiczna

funkcja postaci $f (x) = \log_{a} x$ , gdzie $x > 0$ oraz $a > 0$ i $a \neq 1$

monotoniczność funkcji logarytmicznej

$f (x) = \log_{a} x$ dla $a \in (0, 1)$ jest malejąca

Wprowadzenie

Aplet

Słownik