Przeczytaj

Funkcją logarytmiczną nazywamy funkcję określoną wzorem $f (x) = \log_{a} x$ , gdzie $a \in (0, 1) \cup (1, \infty)$ oraz $x > 0$ .

W materiale omówimy własności wykresu funkcji określonej wzorem $f (x) = \log_{a} x$ dla przypadku, gdy $a \in (1, \infty)$ .

Naszkicujmy w jednym układzie współrzędnych wykresy funkcji zadanych wzorami $f (x) = \log_{3} x$ oraz $g (x) = \log_{\sqrt{2}} x$

W tym celu w tabelach przedstawmy wartości tych funkcji dla kilku argumentów.

$x$	$\frac{1}{3}$	$1$	$3$	$9$
$f (x)$	$- 1$	$0$	$1$	$2$

$x$	$\frac{1}{2}$	$1$	$2$	$4$
$g (x)$	$- 2$	$0$	$2$	$4$

Wykresy tych funkcji przedstawiają się następująco:

R8SXJzRC4KrSm

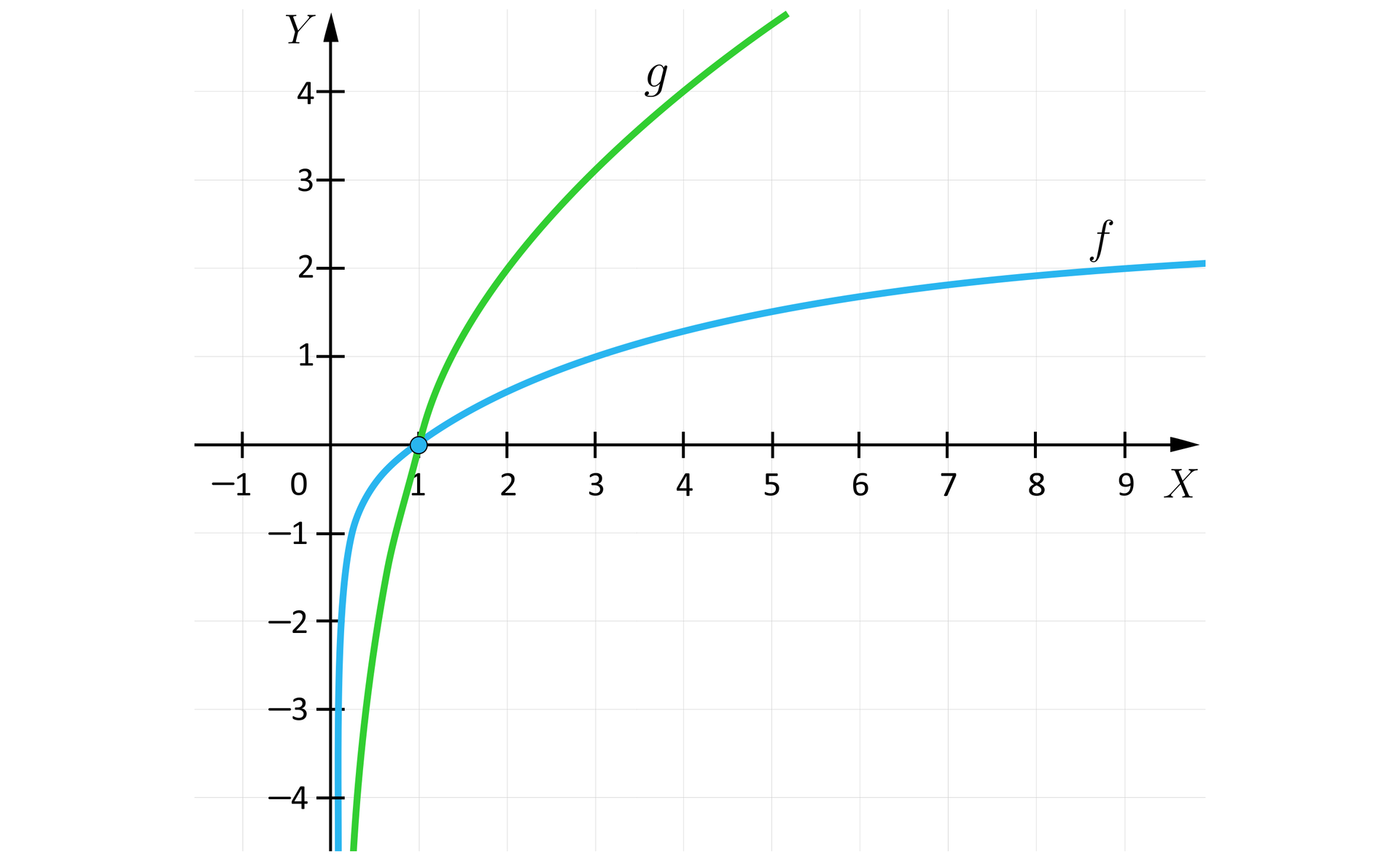
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do dziewięciu oraz z pionową osią Y od minus czterech do czterech. Na płaszczyźnie zaznaczono wykresy funkcji f oraz g. Funkcje te są funkcjami logarytmicznymi, obie przechodzą przez punkt o współrzędnych 1,0 - wykresy przecinają się w tym punkcie. Wykres funkcji f jest bardziej wypłaszczony. Dla obu funkcji oś Y jest asymptotą pionową. Obie funkcje są rosnące.

Na podstawie wykresów funkcji możemy określić własności wykresu funkcji zadanej wzorem $f (x) = \log_{a} x$ dla $a \in (1, \infty)$ :

asymptotą wykresu funkcji jest prosta $x = 0$ ,
wykres funkcji zawsze przechodzi przez punkt $(1, 0)$ , bo $\log_{a} 1 = 0$ ,
wykres funkcji znajduje się w $I$ i $IV$ ćwiartce układu współrzędnych, bo funkcja jest określona tylko dla $x > 0$ ,
$f (x) < 0$ dla $x \in (0, 1)$ oraz $f (x) > 0$ dla $x \in (1, \infty)$ .

Wymienione pierwsze trzy własności wykresu funkcji logarytmicznej $f (x) = \log_{a} x$ dla $a \in (1, \infty)$ nie ulegają zmianie, gdy podstawa $a$ logarytmu jest liczbą z przedziału $(0, 1)$ .

Ciekawostka

Wykresy funkcji logarytmicznych określonych wzorami $f (x) = \log_{a} x$ oraz $g (x) = \log_{\frac{1}{a}} x$ są symetryczne względem osi $X$ układu współrzędnych.

Dowód:

Wzór funkcji $g (x) = \log_{\frac{1}{a}} x$ możemy zapisać w postaci $g (x) = \log_{a^{- 1}} x$ .

Zatem $g (x) = \log_{a^{- 1}} x = \log_{a} x^{- 1} = - \log_{a} x$ .

Jeżeli $g (x) = - f (x)$ , to wykresy funkcji $f$ i $g$ są symetryczne względem osi $X$ .

Mając dany punkt, który należy do wykresu funkcjiwykres funkcjiwykresu funkcji logarytmicznej, możemy wyznaczyć jej wzór.

Przykład 1

Wykres funkcji określonej wzorem $f (x) = \log_{a} x$ przedstawiono na poniższym rysunku. Wyznaczymy wzór tej funkcji.

R7yGzXvOBchHV

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do dziewięciu oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie zaznaczono wykres funkcji f. Funkcja ta jest funkcją logarytmiczną. Przechodzi przez punkt o współrzędnych 1,0. Oś Y jest asymptotą pionową funkcji. Funkcja jest rosnąca.

Z rysunku możemy odczytać, że do wykresu tej funkcji należy punkt o współrzędnych $(8, 2)$ .

Chcąc wyznaczyć wartość $a$ we wzorze funkcji logarytmicznejfunkcja logarytmicznafunkcji logarytmicznej, musimy rozwiązać równanie:

$2 = \log_{a} 8$ , zatem $a^{2} = 8$ .

Wartość $a = 2 \sqrt{2}$ lub $a = - 2 \sqrt{2}$ .

Ponieważ $a > 0$ , zatem funkcję $f$ opisujemy za pomocą wzoru $f (x) = \log_{2 \sqrt{2}} x$ .

Przykład 2

Do wykresu funkcji logarytmicznej określonej wzorem $f (x) = \log_{a} x$ należy punkt o współrzędnych $(4, 9)$ . Wyznaczymy wzór tej funkcji.

W celu wyznaczenia wzoru funkcji, współrzędne punktu $(4, 9)$ podstawiamy do wzoru $f (x) = \log_{a} x$ i rozwiązujemy równanie:

$\log_{a} 9 = 4$

Z równania otrzymujemy, że $a = \sqrt{3}$ lub $a = - \sqrt{3}$ .

Ponieważ $a > 0$ , zatem $a = \sqrt{3}$ .

Wzór funkcji jest postaci $f (x) = \log_{\sqrt{3}} x$ .

Przykład 3

Do wykresu funkcji logarytmicznej określonej wzorem $f (x) = \log_{4} (a x - b)$ należą punkty o współrzędnych $(6, 1)$ oraz $(\frac{9}{4}, - 1)$ .

Wyznaczymy wzór tej funkcji.

W celu wyznaczenia wartości $a$ i $b$ musimy rozwiązać układ równań:

$\{\begin{cases} \log_{4} (6 a - b) = 1 \\ \log_{4} (\frac{9}{4} a - b) = - 1 \end{cases}$ .

Układ przekształcamy do postaci: $\{\begin{cases} 6 a - b = 4 \\ \frac{9}{4} a - b = \frac{1}{4} \end{cases}$ .

Rozwiązaniem układu równań jest para liczb $a = 1$ i $b = 2$ .

Zatem wzór funkcji zapisujemy w postaci: $f (x) = \log_{4} (x - 2)$ .

Sprawdzenie:

$f (6) = \log_{4} (6 - 2) = \log_{4} 4 = 1$

$f (\frac{9}{4}) = \log_{4} (\frac{9}{4} - 2) = \log_{4} \frac{1}{4} = - 1$ .

Wykorzystując własności wykresu funkcji logarytmicznej możemy wyznaczyć argumenty, dla których funkcja przyjmuje wartości dodatnie lub ujemne.

Przykład 4

Wyznaczymy, dla jakich argumentów funkcja określona wzorem $f (x) = \log_{5} (2 x - 1)$ przyjmuje wartości ujemne.

W celu ustalenia dziedziny logarytmu rozwiązujemy nierówność $2 x - 1 > 0$ , zatem $x \in (\frac{1}{2}, \infty)$ .

Jeżeli $f (x) < 0$ to $2 x - 1 > 0$ oraz $2 x - 1 < 1$ , zatem $x \in (\frac{1}{2}, 1)$ .

Szukamy części wspólnej rozwiązania oraz dziedziny funkcji.

Zatem $x \in (\frac{1}{2}, 1)$ .

Przykład 5

Wyznaczymy, dla jakich argumentów funkcja określona wzorem $f (x) = \log_{3} (x^{2} - x)$ przyjmuje wartości dodatnie.

W celu ustaleniea dziedziny logarytmu rozwiązujemy nierówność $x^{2} - x > 0$ , więc $x \in (- \infty, 0) \cup (1, \infty)$

Jeżeli $f (x) > 0$ , to rozwiązujemy nierówność: $x^{2} - x > 1$ .

Rozwiązaniem nierówności jest zbiór $x \in (- \infty, \frac{1 - \sqrt{5}}{2}) \cup (\frac{1 + \sqrt{5}}{2}, \infty)$ .

Szukamy części wspólnej rozwiązania oraz dziedziny funkcji.

Zatem funkcja przyjmuje wartości dodatnie dla argumentów $x \in (- \infty, \frac{1 - \sqrt{5}}{2}) \cup (\frac{1 + \sqrt{5}}{2}, \infty)$ .

Słownik

funkcja logarytmiczna

funkcja określona wzorem $f (x) = \log_{a} x$ , gdzie $a \in (0, 1) \cup (1, \infty)$ oraz $x > 0$

wykres funkcji

zbiór punktów $(x, y)$ płaszczyzny, które spełniają zależność $y = f (x)$

Wprowadzenie

Aplet

Słownik