Przeczytaj

Pojęcie silni – przypomnienie

Niech $n$ będzie liczbą naturalną.

Przypomnijmy, że symbol $n!$ (czytamy: $n$ silnia) to:

$1$ , gdy $n = 0$ lub $n = 1$
$1 \cdot 2 \cdot 3 \cdot . . . \cdot (n - 1) \cdot n$ , gdy $n \geq 2$

Przykład 1

Możemy zapisać:

$0! = 1$

$1! = 1$

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120$

$\frac{n!}{(n - 1)!} = \frac{(n - 1)! \cdot n}{(n - 1)!} = n$

Symbol Newtona

Definicja: Symbol Newtona

Symbolem Newtona (współczynnikiem dwumianowym Newtona) nazywamy liczbę $(\begin{array}{l} n \\ k \end{array})$ , gdzie $n \in ℕ$ , $k \in ℕ$ i $k \leq n$ .

Zapis $(\begin{matrix} n \\ k \end{matrix})$ czytamy: $n$ po $k$ lub $n$ nad $k$ .

Symbol Newtona wyraża się wzorem:

(\begin{matrix} n \\ k \end{matrix}) = \frac{n!}{k! \cdot (n - k)!}

Symbol Newtonasymbol NewtonaSymbol Newtona można też wyrazić wzorem rekurencyjnym:

(\begin{array}{l} n \\ k \end{array}) = \{\begin{cases} 1 & dla k = 0 lub k = n \\ (\begin{matrix} n - 1 \\ k - 1 \end{matrix}) + (\begin{matrix} n - 1 \\ k \end{matrix}) & dla 0 < k < n \end{cases}

Przykład 2

Możemy zapisać:

$(\begin{matrix} n \\ 0 \end{matrix}) = 1$

$(\begin{matrix} n \\ 1 \end{matrix}) = \frac{n!}{1! \cdot (n - 1)!} = \frac{(n - 1)! \cdot n}{(n - 1)!} = n$

$(\begin{matrix} n \\ n \end{matrix}) = 1$

Przykład 3

Możemy zapisać:

$(\begin{matrix} 6 \\ 2 \end{matrix}) = \frac{6!}{2! \cdot (6 - 2)!} = \frac{4! \cdot 5 \cdot 6}{1 \cdot 2 \cdot 4!} = \frac{30}{2} = 15$

$(\begin{matrix} 7 \\ 4 \end{matrix}) = \frac{7!}{4! \cdot (7 - 4)!} = \frac{4! \cdot 5 \cdot 6 \cdot 7}{4! \cdot 3!} = \frac{210}{1 \cdot 2 \cdot 3} = 35$

$(\begin{matrix} 10 \\ 9 \end{matrix}) = \frac{10!}{9! \cdot (10 - 9)!} = \frac{9! \cdot 10}{9! \cdot 1!} = 10$

Symbol Newtona można też obliczyć z „uproszczonego” wzoru:

$(\begin{matrix} n \\ k \end{matrix}) = \frac{n \cdot (n - 1) \cdot . . . \cdot (n - k + 1)}{1 \cdot 2 \cdot . . . \cdot k}$ , gdy $0 < k < n$

Przykład 4

Korzystając z „uproszczonego” wzoru na symbol Newtonasymbol Newtonasymbol Newtona obliczymy $(\begin{matrix} 8 \\ 3 \end{matrix})$ i $(\begin{matrix} 10 \\ 7 \end{matrix})$ .

$(\begin{matrix} 8 \\ 3 \end{matrix}) = \frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3} = 56$

$(\begin{matrix} 10 \\ 7 \end{matrix}) = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7} = 120$

Własności symbolu Newtona

Poznamy teraz kilka podstawowych twierdzeń związanych z symbolem Newtona.

Własność 1 symbolu Newtona

Twierdzenie: Własność 1 symbolu Newtona

Dla każdej liczby naturalnej $n$ i każdej liczby naturalnej $k$ takiej, że $0 \leq k \leq n$ spełniona jest równość:

(\begin{matrix} n \\ k \end{matrix}) = (\begin{matrix} n \\ n - k \end{matrix})

Dowód

Zauważmy, że $k = n - (n - k)$ . Zatem:

(\begin{matrix} n \\ k \end{matrix}) = \frac{n!}{k! \cdot (n - k)!} = \frac{n!}{(n - (n - k))! \cdot (n - k)!} = (\begin{matrix} n \\ n - k \end{matrix})

Przykład 5

Korzystając z powyższego twierdzenia możemy zapisać:

$(\begin{matrix} 10 \\ 2 \end{matrix}) = (\begin{matrix} 10 \\ 10 - 2 \end{matrix}) = (\begin{matrix} 10 \\ 8 \end{matrix})$

$(\begin{matrix} 6 \\ 4 \end{matrix}) = (\begin{matrix} 6 \\ 6 - 4 \end{matrix}) = (\begin{matrix} 6 \\ 2 \end{matrix})$

$(\begin{matrix} n \\ 7 \end{matrix}) = (\begin{matrix} n \\ n - 7 \end{matrix})$ , gdy $n \geq 7$

Własność 2 symbolu Newtona

Twierdzenie: Własność 2 symbolu Newtona

Dla każdej liczby naturalnej $n > 1$ i każdej liczby naturalnej $k$ takiej, że $1 \leq k \leq n$ spełniona jest równość:

k \cdot (\begin{matrix} n \\ k \end{matrix}) = n \cdot (\begin{matrix} n - 1 \\ k - 1 \end{matrix})

Dowód

Oznaczmy przez $L$ – lewą stronę dowodzonej równości, przez $P$ – prawą stronę równości.

Korzystamy z definicji symbolu Newtona.

L = k \cdot (\begin{matrix} n \\ k \end{matrix}) = \frac{k \cdot n!}{k! \cdot (n - k)!}

Przekształcamy odpowiednio zapisaną równość.

L = \frac{k \cdot (n - 1)! \cdot n}{k! \cdot ((n - 1) - (k - 1))!} = \frac{n \cdot k}{k} \cdot \frac{(n - 1)!}{(k - 1)! \cdot ((n - 1) - (k - 1))!}

Korzystamy z tego, że $\frac{(n - 1)!}{(k - 1)! \cdot ((n - 1) - (k - 1))} = (\begin{matrix} n - 1 \\ k - 1 \end{matrix})$ i skracamy przez $k$ .

L = n \cdot (\begin{matrix} n - 1 \\ k - 1 \end{matrix})

L = P

Przykład 6

Korzystając z powyższego twierdzenia, obliczymy $4 (\begin{matrix} 6 \\ 4 \end{matrix})$ oraz $5 (\begin{matrix} 10 \\ 5 \end{matrix})$ .

$4 (\begin{matrix} 6 \\ 4 \end{matrix}) = 6 (\begin{matrix} 6 - 1 \\ 4 - 1 \end{matrix}) = 6 (\begin{matrix} 5 \\ 3 \end{matrix}) = 6 \cdot \frac{5!}{3! \cdot 2!} = 6 \cdot \frac{4 \cdot 5}{2} = 60$

$5 (\begin{matrix} 10 \\ 5 \end{matrix}) = 10 (\begin{matrix} 9 \\ 4 \end{matrix}) = 10 \cdot \frac{9!}{4! \cdot 5!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6}{24} = 1260$

Własność 3 symbolu Newtona

Twierdzenie: Własność 3 symbolu Newtona

Dla każdej liczby naturalnej $n$ i każdej liczby naturalnej $k$ takiej, że $0 \leq k \leq n$ zachodzi równość:

(\begin{matrix} n \\ k \end{matrix}) + (\begin{matrix} n \\ k + 1 \end{matrix}) = (\begin{matrix} n + 1 \\ k + 1 \end{matrix})

Dowód

Oznaczmy przez $L$ – lewą stronę dowodzonej równości, przez $P$ – prawą stronę równości.

L = (\begin{matrix} n \\ k \end{matrix}) + (\begin{matrix} n \\ k + 1 \end{matrix}) = \frac{n!}{k! \cdot (n - k)!} + \frac{n!}{(k + 1)! \cdot (n - k - 1)!}

Rozszerzamy pierwszy składnik przez $k + 1$ , a drugi przez $n - k$ , aby w konsekwencji uzyskać wspólny mianownik ułamków.

L = \frac{n! \cdot (k + 1)}{k! \cdot (k + 1) \cdot (n - k)!} + \frac{n! \cdot (n - k)}{(k + 1)! \cdot (n - k - 1)! \cdot (n - k)}

Wykorzystujemy własności silni.

L = \frac{n! \cdot (k + 1)}{(k + 1)! \cdot (n - k)!} + \frac{n! \cdot (n - k)}{(k + 1)! \cdot (n - k)!}

Dodajemy ułamki.

L = \frac{n! \cdot (k + 1) + n! \cdot (n - k)}{(k + 1)! \cdot (n - k)!}

Wyłączamy $n!$ przed nawias i korzystamy z własności silni.

L = \frac{n! \cdot (k + 1 + n - k)}{(k + 1)! \cdot (n - k)!} = \frac{n! \cdot (n + 1)}{(k + 1)! \cdot (n - k)!}

L = \frac{(n + 1)!}{(k + 1)! \cdot ((n + 1) - (k + 1))!} = (\begin{matrix} n + 1 \\ k + 1 \end{matrix})

L = P

Przykład 7

Korzystając z powyższego twierdzenia, można zapisać:

$(\begin{matrix} 8 \\ 3 \end{matrix}) + (\begin{matrix} 8 \\ 4 \end{matrix}) = (\begin{matrix} 9 \\ 4 \end{matrix})$

$(\begin{matrix} 10 \\ 2 \end{matrix}) + (\begin{matrix} 10 \\ 3 \end{matrix}) = (\begin{matrix} 11 \\ 3 \end{matrix})$

$(\begin{matrix} n \\ 6 \end{matrix}) + (\begin{matrix} n \\ 7 \end{matrix}) = (\begin{matrix} n + 1 \\ 7 \end{matrix})$

Związek symbolu Newtona z trójkątem Pascala

Zauważmy, że kolejnym wyrazom trójkąta Pascala można przyporządkować odpowiednie symbole Newtona. W trójkącie Pascala każdy wyraz (poza skrajnym) jest sumą dwu wyrazów stojących bezpośrednio nad nim.

Schemat ten odpowiada zależności

(\begin{matrix} n \\ k \end{matrix}) = (\begin{matrix} n - 1 \\ k - 1 \end{matrix}) + (\begin{matrix} n - 1 \\ k \end{matrix})

zapisanej we wzorze rekurencyjnym.

R1TNLmfUPDrxC

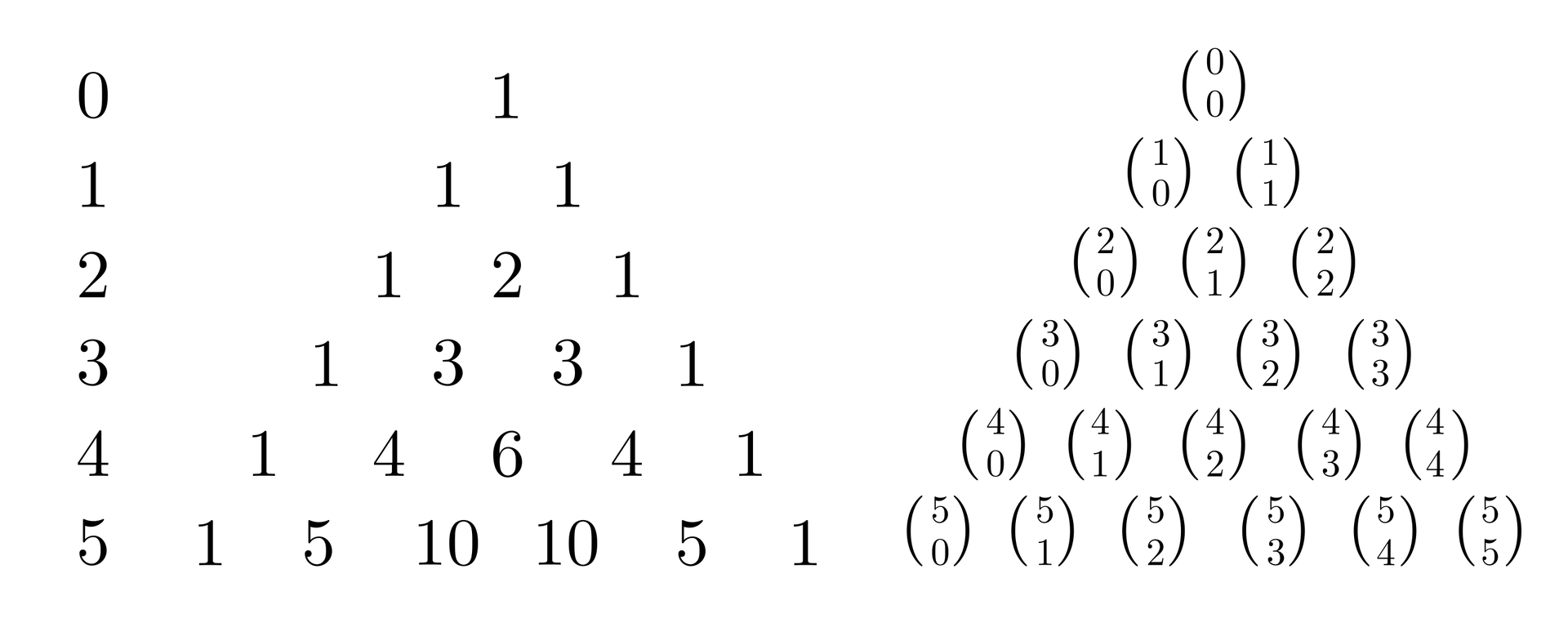
Zdjęcie przedstawia związek symbolu z trójkątem pascala.

Wiemy już, że suma wyrazów w $n$ –tym wierszu trójkąta Pascala jest równa $2^{n}$ .

Wynika stąd ważna własność symbolu Newtona:

(\begin{matrix} n \\ 0 \end{matrix}) + (\begin{matrix} n \\ 1 \end{matrix}) + . . . + (\begin{matrix} n \\ n - 1 \end{matrix}) + (\begin{matrix} n \\ n \end{matrix}) = 2^{n}

Przykład 8

Rozwiążemy równanie

$4 \cdot [(\begin{array}{l} 5 \\ 0 \end{array}) + (\begin{array}{l} 5 \\ 1 \end{array}) + (\begin{array}{l} 5 \\ 2 \end{array}) + (\begin{array}{l} 5 \\ 3 \end{array}) + (\begin{array}{l} 5 \\ 4 \end{array}) + (\begin{array}{l} 5 \\ 5 \end{array})] = 8^{x}$

Przekształcając lewą stronę równania, skorzystamy ze wzoru na sumę kolejnych symboli Newtona.

$4 \cdot 2^{5} = 8^{x}$

Liczby $4$ i $8$ zapisujemy jako potęgi liczby $2$ .

$2^{2} \cdot 2^{5} = 2^{3 x}$

$2^{7} = 2^{3 x}$

Porównujemy wykładniki potęg o tych samych podstawach.

$7 = 3 x$

$x = \frac{7}{3} = 2 \frac{1}{3}$

Odpowiedź:

Rozwiązaniem równania jest liczba $2 \frac{1}{3}$ .

Słownik

symbol Newtona

to liczba $(\begin{matrix} n \\ k \end{matrix})$ , gdzie $n \in ℕ$ , $k \in ℕ$ i $k \leq n$

Wprowadzenie

Animacja

Pojęcie silni – przypomnienie

Symbol Newtona

Własności symbolu Newtona

Związek symbolu Newtona z trójkątem Pascala

Słownik