Przeczytaj

Przypomnijmy, że współrzędne punktów podajemy w nawiasie okrągłym. Na przykład współrzędne punktu $A$ , który na osi liczbowej odpowiada liczbie $5$ , oznaczymy jako $A = (5)$ . Dla odróżnienia od współrzędnych punktu współrzędne wektora będziemy podawać w nawiasie kwadratowym.

R15DiaAUpmv0Z

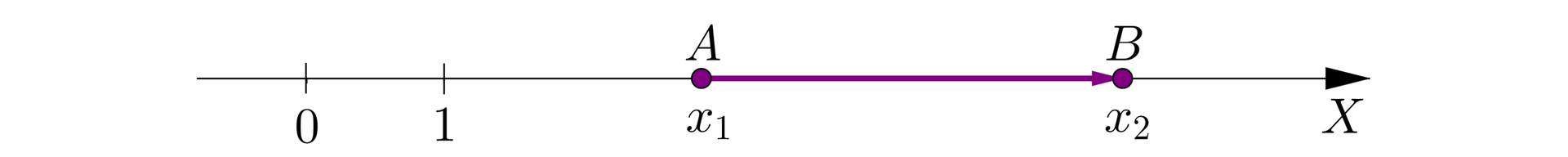
Ilustracja przedstawia poziomą oś X. Po lewej stronie osi zaznaczone są punkty zero i jeden. Mniej więcej na środku zaznaczony jest punkt A równy X 1, na prawo punkt B równy X 2. Z punktu A do punktu B poprowadzony jest wektor AB.

Współrzędną wektora na osiwspółrzędna wektora na osiWspółrzędną wektora na osi liczbowej definiujemy jako różnicę współrzędnej końca i współrzędnej początku.

Jeśli $A = (x_{1})$ , $B = (x_{2})$ , to współrzędną wektora $\vec{A B}$ jest liczba $x_{2} - x_{1}$ , co zapisujemy $\vec{A B} = [x_{2} - x_{1}]$ .

Możemy zauważyć, że wektor zaczepiony w początku osi liczbowej ma współrzędną równą współrzędnej końca tego wektora. Ponadto wektor zerowy ma współrzędną na osi równą zeru: $\vec{0} = [0]$ .

RKME9qArWBs4l

Ilustracja przedstawia poziomą oś X. Po lewej stronie osi zaznaczone są punkty zero i jeden. Zaznaczony jest punkt O równy 0 oraz po prawej stronie punkt P równy X. Z punktu O do punktu P poprowadzony jest wektor OP równy x.

Przykład 1

Jeśli $A = (- 5)$ , $B = (- 3)$ , to $\vec{A B} = [- 3 - (- 5)] = [2]$

o równości wektorów

Twierdzenie: o równości wektorów

Dwa wektory na osi liczbowej są równe wtedy i tylko wtedy, gdy mają równe współrzędne.

Dowód

Dowód pozostawiamy jako ćwiczenie.

Przykład 2

Wyznacz wartość parametru $m$ tak, aby wektory o współrzędnych $\vec{u} = [m^{2} - 3]$ i $\vec{v} = [- 2 m - 4]$ były równe.

Zgodnie z powyższym twierdzeniem wektory $\vec{u}$ i $\vec{v}$ będą równe wtedy i tylko wtedy gdy ich współrzędne będą równe, czyli gdy spełnione będzie równanie $m^{2} - 3 = - 2 m - 4$ , które można przekształcić do postaci $m^{2} + 2 m + 1 = 0$ . Po zastosowaniu wzoru skróconego mnożenia otrzymujemy równanie ${(m + 1)}^{2} = 0$ , którego jedynym pierwiastkiem jest $m = - 1$ . Zatem wektory $\vec{u} = [m^{2} - 3]$ i $\vec{v} = [- 2 m - 4]$ są równe dokładnie wtedy, gdy $m = - 1$ .

Poniższe twierdzenia pokazują, jak wyznaczyć współrzędne sumy i różnicy wektorów na osi oraz współrzędną iloczynu wektora i liczby.

suma wektorów

Twierdzenie: suma wektorów

Suma wektorów na osisuma wektorów na osiSuma wektorów na osi ma współrzędną równą sumie współrzędnych dodawanych wektorów: jeśli $\vec{u} = [a_{1}]$ , $\vec{v} = [a_{2}]$ , to $\vec{u} + \vec{v} = [a_{1} + a_{2}]$ .

Dowód

Niech $\vec{u} = \vec{A B}$ , $\vec{v} = \vec{B C}$ , gdzie $A = (x_{1})$ , $B = (x_{2})$ , $C = (x_{3})$ . Wówczas $\vec{u} + \vec{v} = \vec{A B} + \vec{B C} = \vec{A C}$ oraz $\vec{A B} = [x_{2} - x_{1}] = [a_{1}]$ , $\vec{B C} = [x_{3} - x_{2}] = [a_{2}]$ . Zatem $\vec{u} + \vec{v} = \vec{A B} + \vec{B C} = \vec{A C} = [x_{3} - x_{1}] = [(x_{3} - x_{2}) + (x_{2} - x_{1})] =$ $= [a_{2} + a_{1}]$ .

wektory przeciwne

Twierdzenie: wektory przeciwne

Współrzędna wektora przeciwnegowektor przeciwnywektora przeciwnego do wektora $\vec{u}$ jest liczbą przeciwną do współrzędnej wektora $\vec{u}$ : jeśli $\vec{u} = [a]$ , to $- \vec{u} = [- a]$ .

Dowód

Jeśli $\vec{u} = \vec{A B}$ , gdzie $A = (x_{1})$ , $B = (x_{2})$ , to $\vec{A B} = [x_{2} - x_{1}] = [a]$ oraz $- \vec{u} = \vec{B A} = [x_{1} - x_{2}] = [- (x_{2} - x_{1})] = [- a]$ .

różnica wektorów

Twierdzenie: różnica wektorów

Współrzędna różnicy wektorów na osiróżnica wektorów na osiróżnicy wektorów na osi jest równa różnicy odejmowanych wektorów: jeśli $\vec{u} = [a_{1}], \vec{v} = [a_{2}]$ , to $\vec{u} - \vec{v} = [a_{1} - a_{2}]$ .

Dowód

$\vec{u} - \vec{v} = \vec{u} + (- \vec{v}) = [a_{1}] + [- a_{2}] = [a_{1} + (- a_{2})] = [a_{1} - a_{2}]$ .

iloczyn wektora przez liczbę

Twierdzenie: iloczyn wektora przez liczbę

Współrzędna iloczynu wektora przez liczbęiloczyn wektora przez liczbęiloczynu wektora przez liczbę jest równa iloczynowi tej liczby i współrzędnej danego wektora: jeśli $\vec{u} = [a]$ , to $k \vec{u} = [k a]$ .

Dowód

Dowód pozostawiamy jako ćwiczenie.

Przykład 3

Niech $\vec{u} = [- 3]$ , $\vec{v} = [2]$ . Obliczymy $\vec{u} + \vec{v}$ , $\vec{u} - \vec{v}$ , $3 \vec{u} - 2 \vec{v}$ .

$\vec{u} + \vec{v} = [- 3] + [2] = [- 3 + 2] = [- 1]$

$\vec{u} - \vec{v} = [- 3] - [2] = [- 3 - 2] = [- 5]$

$3 \vec{u} - 2 \vec{v} = 3 \cdot [- 3] - 2 \cdot [2] = [- 9] - [4] = [- 9 - 4] = [- 13]$

Słownik

współrzędna wektora na osi

różnica między współrzędną końca wektora i współrzędną początku wektora; dla $A = (x_{1})$ , $B = (x_{2})$ wektor $\vec{A B}$ ma współrzędną $[x_{2} - x_{1}]$

suma wektorów na osi

twierdzenie orzekające, że współrzędna sumy wektorów na osi jest równa sumie współrzędnych wektorów składowych

różnica wektorów na osi

twierdzenie orzekające, że współrzędna różnicy wektorów na osi jest równa różnicy współrzędnych wektorów składowych

wektor przeciwny

twierdzenie orzekające, że współrzędna wektora przeciwnego do danego jest liczbą przeciwną do współrzędnej danego wektora

iloczyn wektora przez liczbę

twierdzenie orzekające, że współrzędna iloczynu wektora i liczby jest równa iloczynowi współrzędnej danego wektora przez tę liczbę

Wprowadzenie

Infografika

Słownik