Przeczytaj
Wykonanie równocześnie kilku przekształceń wykresu funkcji logarytmicznejfunkcji logarytmicznej powoduje zmianę zarówno położenia samego wykresu względem osi układu współrzędnych, jak i zmianę własności tej funkcji.
Omówimy przesunięcie wykresu funkcji logarytmicznej określonej wzorem , gdzie , wzdłuż osi oraz osi układu współrzędnych.
Wykres funkcji określonej wzorem otrzymujemy przez przesunięcie wykresu funkcji o jednostek w prawo () lub o jednostek w lewo () oraz o jednostek w górę () lub o jednostek w dół ().
Naszkicujemy w jednym układzie współrzędnych wykresy funkcji określonych wzorami oraz . W tym celu w tabelach przedstawimy wartości tych funkcji dla kilku argumentów.
Wykresy tych funkcji przedstawiają się następująco:
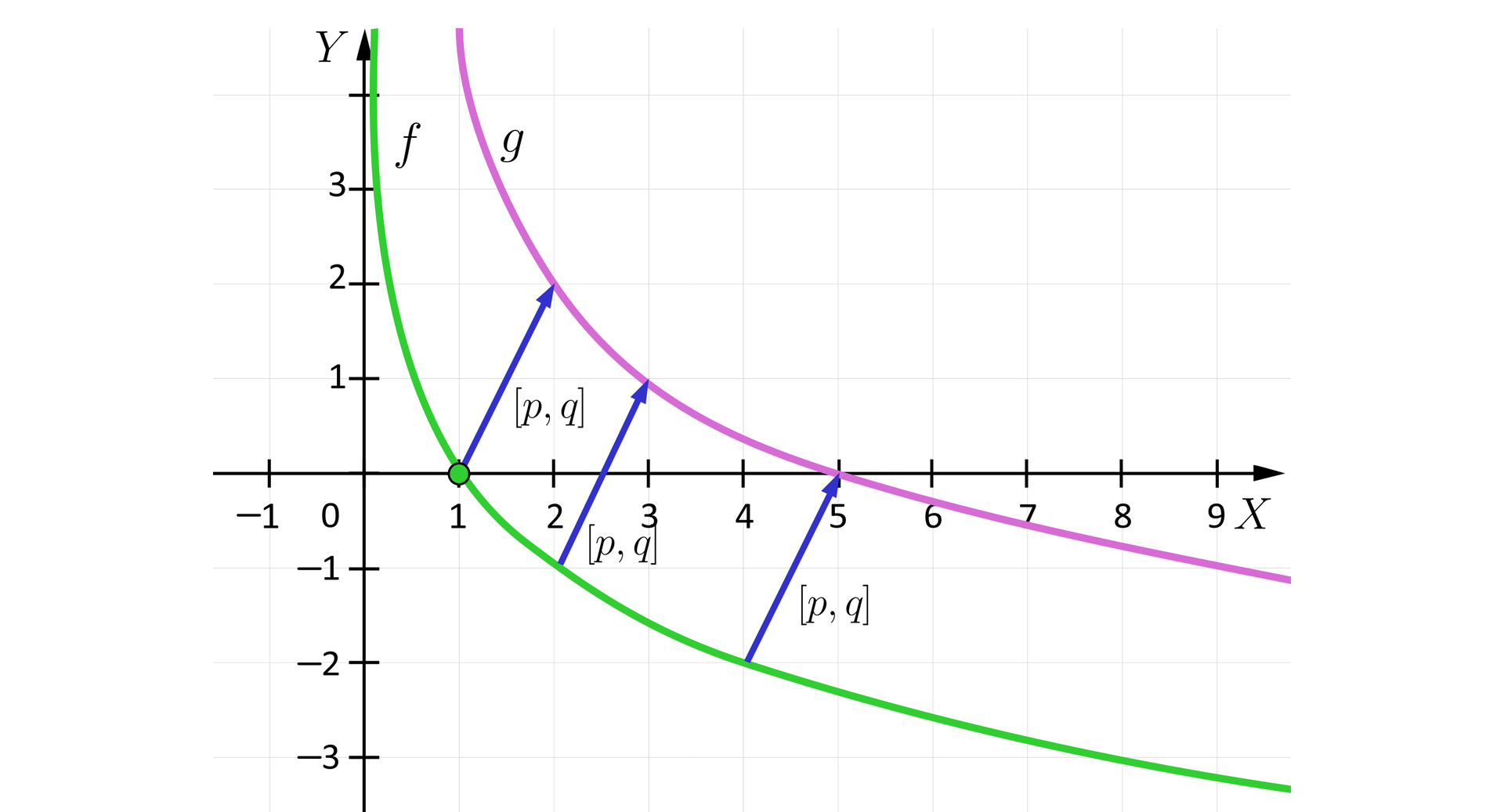
Analizując położenie wykresów oraz wzory tych funkcji możemy zauważyć, że:
wykres funkcji możemy otrzymać przez przesunięcie wykresu funkcji o jednostkę w prawo oraz jednostki w górę,
dziedziną funkcji jest zbiór , a dziedziną funkcji jest zbiór ,
zbiorem wartości obu funkcji jest zbiór liczb rzeczywistych,
miejscem zerowym funkcji jest , a miejscem zerowym funkcji jest ,
asymptotą wykresu funkcji jest prosta , a asymptotą wykresu funkcji jest prosta ,
funkcja przyjmuje wartości ujemne tylko dla argumentów większych od , a funkcja przyjmuje wartości ujemne tylko dla argumentów większych od ,
funkcja przyjmuje wartości dodatnie tylko dla argumentów , a funkcja przyjmuje wartości dodatnie tylko dla argumentów .
Asymptotą wykresu funkcji określonej wzorem jest prosta o równaniu .
Mając dany wzór funkcji przed przekształceniem jej wykresu oraz podane przekształcenie, możemy wyznaczyć wzór funkcji po przesunięciu jej wykresu wzdłuż osi układu współrzędnychprzesunięciu jej wykresu wzdłuż osi układu współrzędnych.
Wykres funkcji określonej wzorem przesunięto wzdłuż osi o jednostki w lewo oraz wzdłuż osi o jednostki w dół. Wyznaczymy wzór funkcji otrzymanej po przesunięciu wykresu.
Wzór funkcji logarytmicznej po przesunięciu wykresu wzdłuż osi oraz osi zapisujemy w postaci .
Z zadania wynika, że oraz .
Zatem wzór funkcji po przekształceniach przyjmuje postać .
Na rysunku przedstawiono wykres funkcji logarytmicznej określonej wzorem .

Wyznaczymy:
a) równanie asymptoty oraz dziedzinę tej funkcji,
b) miejsce zerowe tej funkcji,
c) argumenty, dla których funkcja przyjmuje wartości niedodatnie.
Rozwiązania:
a) Ponieważ , zatem asymptotą wykresu funkcji jest prosta o równaniu .
Dziedziną tej funkcji jest zbiór .
b) Chcąc wyznaczyć miejsce zerowe tej funkcji, rozwiążemy równanie .
Po rozwiązaniu równania otrzymujemy . Uwzględniając, że dziedziną funkcji jest zbiór , potwierdzamy, że miejscem zerowym tej funkcji jest liczba .
c) Z wykresu możemy odczytać, że dla .
Z wykresu funkcji logarytmicznej możemy odczytać własności potrzebne do wyznaczenia jej wzoru.
Na wykresie przedstawiono funkcję określoną wzorem . Wyznaczymy wzór tej funkcji.
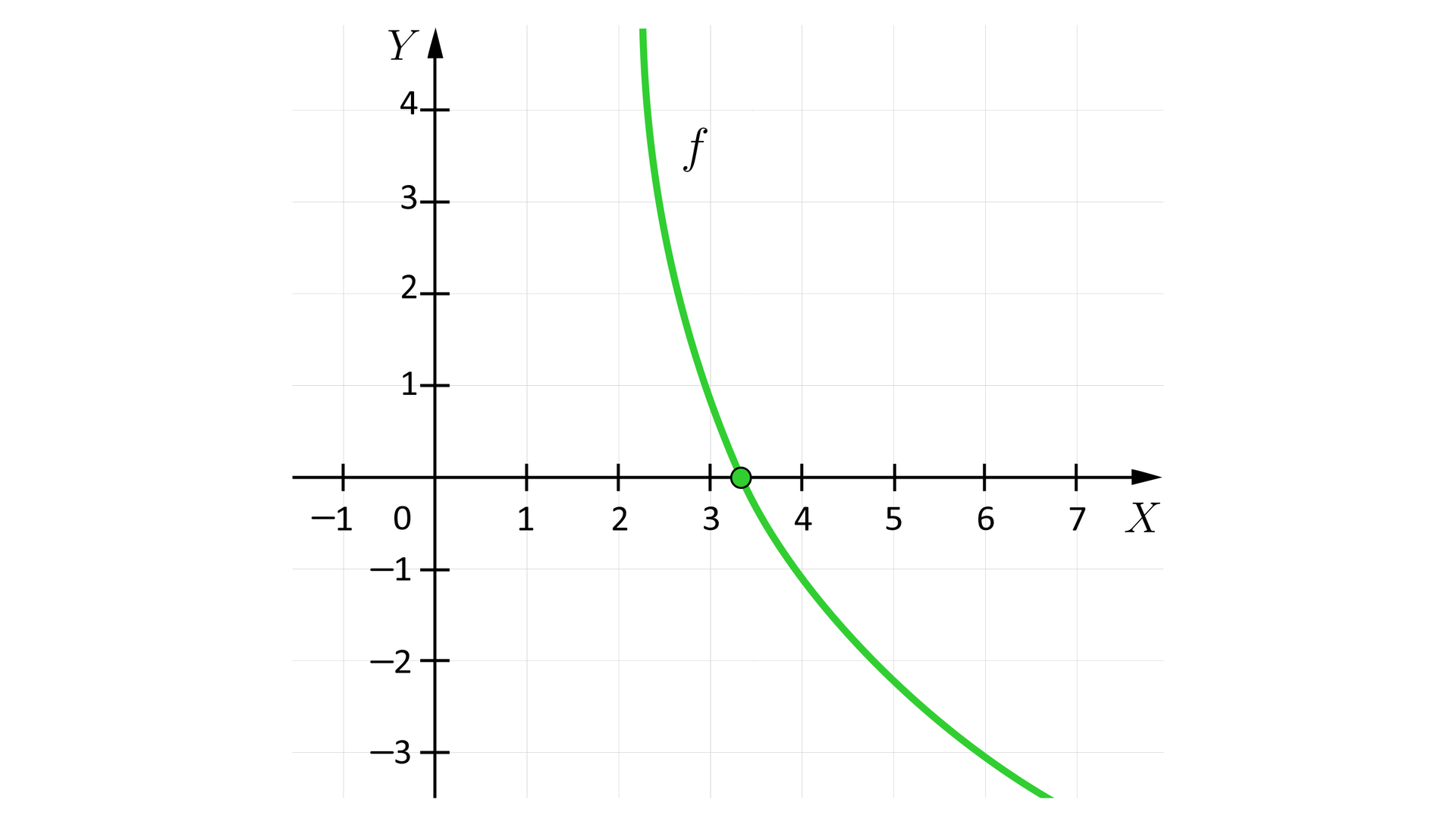
Z wykresu możemy odczytać, że:
asymptotą wykresu funkcji jest prosta , zatem ,
do wykresu funkcji należy punkt o współrzędnych , zatem, w celu wyznaczenia wartości rozwiązujemy równanie .
Korzystając z praw działań na logarytmach, równanie możemy zapisać w postaci , a zatem .
Szukana funkcja wyraża się zatem wzorem .
Do wykresu funkcji określonej za pomocą wzoru należą punkty o współrzędnych oraz . Wyznaczymy wartości parametrów i .
W celu wyznaczenia wartości parametrów i zapisujemy układ równań .
Rozwiązanie układu sprowadza się do rozwiązania równania .
Równanie to zapisujemy w postaci , co po przekształceniu jest równoważne równaniu .
Zatem , więc .
Wartość obliczymy z pierwszego równania układu równań.
, więc .
Wzór funkcji przedstawia się następująco: .
Słownik
funkcja określona wzorem , gdzie oraz
przesunięcie wykresu funkcji o jednostek w prawo () lub o jednostek w lewo () oraz o jednostek w górę () lub o jednostek w dół ()