Przeczytaj

W tym materiale zastanowimy się, co to znaczy dodać do siebie nieskończenie wiele liczb i jaki jest wynik tego działania.

Weźmy przykład następujący:

$1 - 1 + 1 - 1 + 1 - 1 + . . .$

Może zrobimy tak:

$(1 - 1) + (1 - 1) + (1 - 1) + . . . = 0 + 0 + 0 . . . = 0$ .

Czyli pogrupowaliśmy po dwa składniki sumy i dodalismy pogrupowane elementy i otrzymalismy $0$ .

A może spróbujemy tak:

$1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 0) + . . . = 1 + 0 + 0 + 0 + . . . = 1$ .

Tu równeż pogrupowaliśmy składniki, ale grupowanie zaczęliśmy od drugiego składnika. Ale tym razem wyszło nam $1$ , czyli wynik inny niż poprzednio.

A może oznaczmy sumę $s = 1 - 1 + 1 - 1 + 1 - 1 + . . .$

Wówczas zauważamy, że $s = 1 - (1 - 1 + 1 - 1 + 1 - 1 + . . .)$ , czyli $s = 1 - s$ , gdyż wyrażenie w nawiasie jest równe $s$ .

Stąd otrzymujemy: $s = \frac{1}{2}$ .

Zauważmy, że za każdym razem, w zależności od przyjętej metody, otrzymujemy inny wynik. To znaczy, że nasze podejście do sumowania nieskończenie wielu elementów jest niepoprawne - nie możemy dostawać różnych wyników przy sumowaniu tych samych elementów ustawionych w tej samej kolejności. Dodajmy, że wszystkie otrzymane wyniki w świetle przyjętej poniżej definicji są BŁĘDNE.

Musimy zdefiniować w taki sposób sumowanie, aby wynik był jednoznaczny.

szeregu liczbowego

Definicja: szeregu liczbowego

Szeregiem o wyrazach $a_{1}, a_{2}, a_{3}, . . .$ nazywamy ciąg, którego kolejnymi wyrazami są sumy początkowych wyrazów ciągu $(a_{n})$ :

$s_{1} = a_{1}$ ,

$s_{2} = a_{1} + a_{2}$ ,

$s_{3} = a_{1} + a_{2} + a_{3}$ ,

...

Liczby $s_{1}, s_{2}, s_{3}, . . .$ nazywane są sumami częściowymi szeregu o wyrazach $a_{1}, a_{2}, a_{3}, . . .$ Szereg o wyrazach $a_{1}, a_{2}, a_{3}, . . .$ oznaczamy symbolem $a_{1} + a_{2} + a_{3} + . . .$ lub symbolem $\sum_{n = 1}^{\infty} a_{n}$ .

Jeżeli ciąg sum częściowych szeregu ma granicę, to nazywamy ją sumą szeregu, jeżeli suma szeregu jest skończona, to szereg nazywamy zbieżnym, jeżeli suma szeregu jest nieskończona lub jeżeli ciąg sum częściowych szeregu nie ma granicy, to szereg nazywamy rozbieżnym. Jeżeli szereg ma sumę skończoną, to oznaczamy ją tak jak szereg $a_{1} + a_{2} + a_{3} + . . .$ lub symbolem $\sum_{n = 1}^{\infty} a_{n}$ .

Przykład 1

Wracamy do przykładu $1 - 1 + 1 - 1 + 1 - 1 + . . . = \sum_{n = 1}^{\infty} {(- 1)}^{n + 1}$ .

Rozwiązanie

Mamy ciąg $a_{n} = {(- 1)}^{n + 1}$ .

Zobaczmy jak wygląda ciąg sum częsciowych:

$s_{1} = 1$ ,

$s_{2} = 1 - 1 = 0$ ,

$s_{3} = 1 - 1 + 1 = 1$ ,

$s_{4} = 1 - 1 + 1 - 1 = 0$ ,

i tak dalej.

Zatem ciąg $(s_{n})$ jest ciągiem $1, 0, 1, 0, 1, 0, . . .$ rozbieżnym.

Zatem szereg $\sum_{n = 1}^{\infty} {(- 1)}^{n + 1}$ jest szeregiem rozbieżnym.

Przykład 2

Zbadamy zbieżność szeregu: $\sum_{n = 1}^{\infty} (\sqrt{n + 1} - \sqrt{n})$ .

Rozwiązanie

Zapiszmy kolejne sumy częściowe ciągu $a_{n} = \sqrt{n + 1} - \sqrt{n}$ :

$s_{1} = \sqrt{2} - \sqrt{1}$ ,

$s_{2} = (\sqrt{2} - \sqrt{1}) + (\sqrt{3} - \sqrt{2}) = \sqrt{3} - \sqrt{1}$ ,

$s_{3} = (\sqrt{2} - \sqrt{1}) + (\sqrt{3} - \sqrt{2}) + (\sqrt{4} - \sqrt{3}) = \sqrt{4} - \sqrt{1}$ ,

...

Zatem wzór ciągu sum częściowych jest następujący:

$s_{n} = (\sqrt{2} - \sqrt{1}) + (\sqrt{3} - \sqrt{2}) + (\sqrt{4} - \sqrt{3}) + \dots + (\sqrt{n + 1} - \sqrt{n}) =$

$= \sqrt{n + 1} - \sqrt{1} = \sqrt{n + 1} - 1$ .

Ponieważ

$\lim_{n \to \infty} s_{n} = \lim_{n \to \infty} (\sqrt{n + 1} - \sqrt{1}) = + \infty$ ,

zatem szereg $\sum_{n = 1}^{\infty} (\sqrt{n + 1} - \sqrt{n})$ jest rozbieżny.

Przykład 3

Zbadamy zbieżność szeregu: $\sum_{n = 1}^{\infty} {(\frac{1}{2})}^{n}$ .

Rozwiązanie

Zapiszmy kolejne sumy częściowe ciągu $a_{n} = {(\frac{1}{2})}^{n}$ :

$s_{1} = \frac{1}{2}$

$s_{2} = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}$

$s_{3} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} = \frac{7}{8}$

Możemy zauważyć, że sumy częściowe to sumy początkowych wyrazów ciągu geometrycznego o pierwszym wyrazie $a_{1} = \frac{1}{2}$ i ilorazie $q = \frac{1}{2}$ . Zatem możemy zastosować wzór na sumę początkowych wyrazówwzór na sumę początkowych wyrazów:

$s_{n} = \frac{1}{2} \frac{1 - {(\frac{1}{2})}^{n}}{1 - \frac{1}{2}}$

czyli

$s_{n} = 1 - {(\frac{1}{2})}^{n}$ .

Ponieważ ciąg $b_{n} = {(\frac{1}{2})}^{n}$ zmierza do $0$ , zatem granicą ciągu $s_{n} = 1 - {(\frac{1}{2})}^{n}$ jest $1$ .

Wobec tego szereg $\sum_{n = 1}^{\infty} {(\frac{1}{2})}^{n}$ jest zbieżny do $1$ .

Ten przykład możemy zwizualizować na poniższym rysunku: w kwadracie o boku $1$ sumujemy pola prostokątów o polach kolejno: $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, . . .$ Łatwo zauważyć, że prostokąty te wypełniają cały kwadrat, czyli nieskończona suma wszystkich pól prostokątów jest równa $1$ .

R1GAAHkxGSIXR

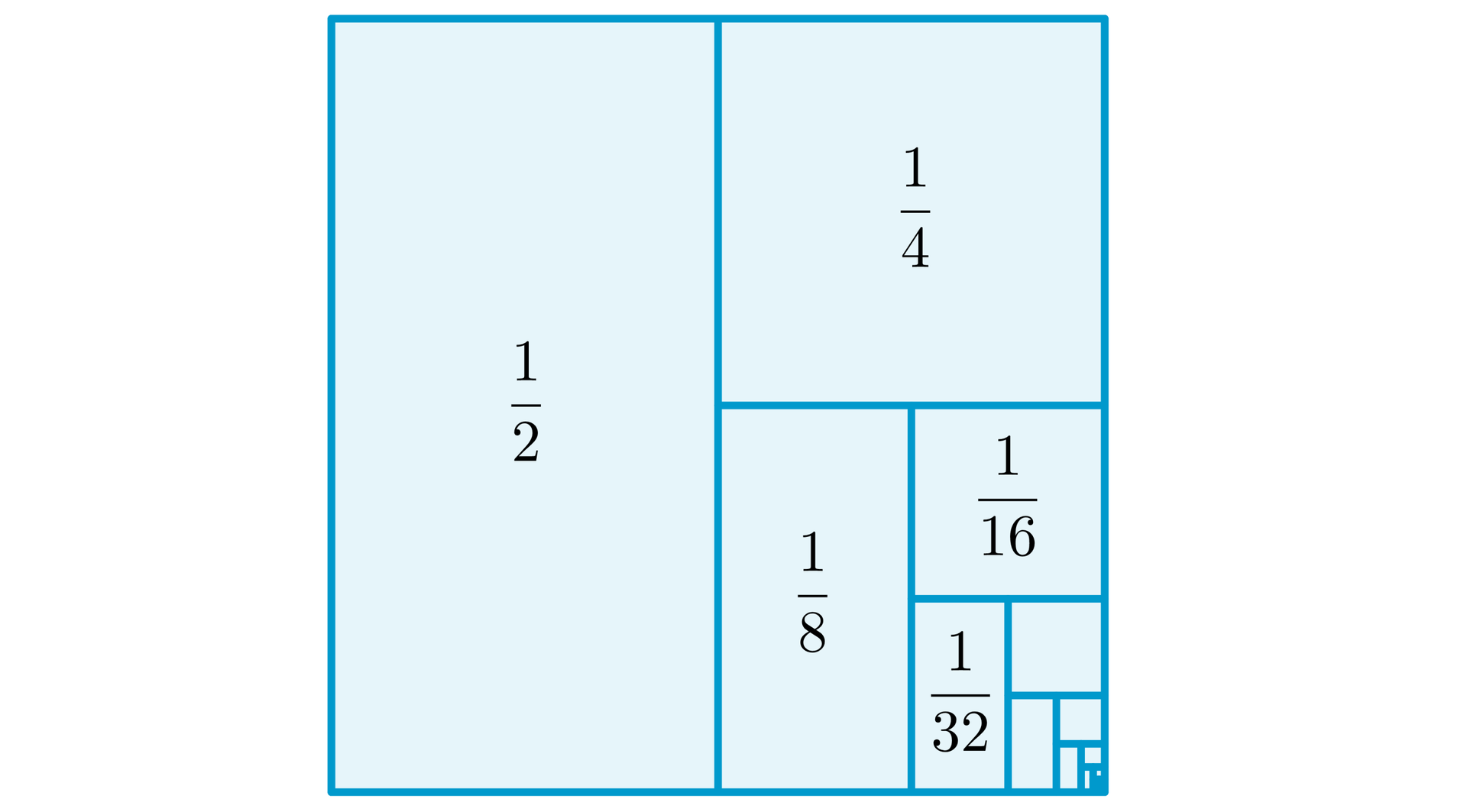
Grafika przedstawia kwadrat, który jest podzielony na mniejsze prostokąty. Pierwszy prostokąt stanowi lewą połowę kwadratu, jego poziomy bok stanowi połowę podstawy kwadratu, a pionowy jest równy bokowi kwadratu. Prostokąt ten jest podpisany 1/2. Z prawej strony tego prostokąta znajduje się kwadrat oraz prostokąt. Kwadrat o boku równym 1/4 boku dużego kwadratu. Kwadrat ten znajduje się w lewym górnym rogu pierwszego kwadratu i jest podpisany 1/4. Pod tym kwadratem znajduje się prostokąt. Pionowa ściana tego prostokąta przylega do prawego boku prostokąta z podpisem 1/2. i ma długość 1/4 boku największego kwadratu. Pozioma ściana tego prostokąta m długość 1/8 boku największego kwadratu. Prostokąt ten jest podpisany 1/8. Z prawej strony tego prostokąta znajduje się kwadrat oraz prostokąt. Kwadrat przylega do kwadratu z podpisem 1/8 oraz kwadratu z podpisem 1/4. Jego boki mają długości równe połowie długości boków kwadratu z podpisem 1/4. Pod tym kwadratem znajduje się prostokąt. Pozioma ściana tego prostokąta ma połowę długości kwadratu z podpisem 1/16, natomiast pionowa ściana połowę długości ściany prostokąta z podpisem 1/8. Prostokąt ten jest podpisany 1/32. Obok tego prostokąta znajduje się kwadrat i prostokąt i są ułożone w taki sam sposób jak poprzednie figury i tak dalej, aż figury są tak małe, że ciężko je rozróżnić.

Przykład 4

Zbadamy zbieżność szeregu: $\sum_{n = 1}^{\infty} \frac{1}{n (n + 1)}$ .

Rozwiązanie

Wykorzystamy znaną zależność: $\frac{1}{n (n + 1)} = \frac{1}{n} - \frac{1}{n + 1}$ .

Wówczas ciąg sum częściowych szeregu $\frac{1}{n (n + 1)} = \frac{1}{n} - \frac{1}{n + 1}$ ma postać:

$s_{n} = \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \dots + \frac{1}{n \cdot (n + 1)} =$

$= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \dots + \frac{1}{n} - \frac{1}{n + 1} = 1 - \frac{1}{n + 1}$ .

Zauważmy, że ciąg $s_{n} = 1 - \frac{1}{n + 1}$ jest zbieżny i jego granicą jest $1$ .

Zatem szereg $\sum_{n = 1}^{\infty} \frac{1}{n (n + 1)}$ jest zbieżny.

Przykład 5

Zbadamy zbieżność szeregu: $\sum_{n = 1}^{\infty} \frac{1}{(2 n - 1) (2 n + 1)}$ .

Rozwiązanie

Wykorzystamy zależność podobną do tej z poprzedniego przykładu: $\frac{1}{(2 n - 1) (2 n + 1)} = \frac{1}{2} (\frac{1}{2 n - 1} - \frac{1}{2 n + 1})$ .

Wówczas ciąg sum częściowych szeregu $\sum_{n = 1}^{\infty} \frac{1}{(2 n - 1) (2 n + 1)}$ ma postać:

$s_{n} = \frac{1}{1 \cdot 3} + \frac{1}{3 \cdot 5} + \dots + \frac{1}{(2 n - 1) (2 n + 1)} =$

$= \frac{1}{2} (1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + \dots + \frac{1}{2 n - 1} - \frac{1}{2 n + 1}) = \frac{1}{2} (1 - \frac{1}{2 n + 1})$

Zauważmy, że ciąg $s_{n} = \frac{1}{2} (1 - \frac{1}{2 n + 1})$ jest zbieżny i jego granicą jest $\frac{1}{2}$ .

Zatem szereg $\sum_{n = 1}^{\infty} \frac{1}{(2 n - 1) (2 n + 1)}$ jest zbieżny.

Przykład 6

Zbadamy zbieżność szeregu: $\sum_{n = 1}^{\infty} n$ .

Rozwiązanie

Ciąg sum częściowych szeregu $\sum_{n = 1}^{\infty} n$ ma postać:

$s_{n} = 1 + 2 + 3 + . . . + n$ ,

czyli

$s_{n} = \frac{n (n + 1)}{2}$

Ciąg $s_{n} = \frac{n (n + 1)}{2}$ jest rozbieżny do $+ \infty$ , zatem szereg $\sum_{n = 1}^{\infty} n$ jest rozbieżny.

Przykład 7

Mając dany ciąg sum częściowych $s_{n} = 2 - \frac{1}{n^{2}}$ szeregu $\sum_{n = 1}^{\infty} a_{n}$ znaleźć wzór ciągu $(a_{n})$ .

Rozwiązanie

Dla liczb naturalnych $n > 1$ możemy zauważyć, że zachodzi następująca zależność:

$s_{n} - s_{n - 1} = (a_{1} + a_{2} + . . . . + a_{n}) - (a_{1} + a_{2} + . . . . + a_{n - 1}) = a_{n}$ .

Zatem w przypadku ciągu z zadania możemy zapisać:

$a_{n} = 2 - \frac{1}{n^{2}} - (2 - \frac{1}{{(n - 1)}^{2}}) = \frac{n^{2} - {(n - 1)}^{2}}{n^{2} {(n - 1)}^{2}} = \frac{2 n - 1}{n^{2} {(n - 1)}^{2}}$ .

Osobno obliczymy wzór na $a_{1}$ :

$a_{1} = s_{1} = 1$ .

Ważne!

Zwróćmy uwagę na to, że w ostatnim przykładzie wyraz $a_{1}$ był obliczany osobno. Dlaczego to jest takie ważne?

Zauważmy, że gdybyśmy wzięli ciąg sum częściowych $s_{n} = 1 - \frac{1}{n^{2}}$ szeregu $\sum_{n = 1}^{\infty} a_{n}$ , to dla liczb naturalnych $n > 1$ , ciąg $(a_{n})$ ma taki sam wzór, jak w przykładzie poprzednim. Ciągi różnią się tylko pierwszym wyrazem.

Słownik

suma początkowych wyrazów ciągu geometrycznego

Jeżeli ciąg $(a_{n})$ jest ciągiem geometrycznym o ilorazie $q$ , to suma $n$ początkowych wyrazów tego ciągu jest równa:

$s_{n} = a_{1} \frac{1 - q^{n}}{1 - q}$ , gdy $q \neq 1$ ,
$s_{n} = n \cdot a_{1}$ , gdy $q = 1$

Wprowadzenie

Infografika

Słownik