Przeczytaj
Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej.
Cosinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.
W trakcie lekcji poznamy i wykorzystamy wzór na jedynkę trygonometrycznąjedynkę trygonometryczną.
Dla dowolnego kąta ostrego w trójkącie prostokątnym zachodzi równość:
Wzór ten nazywamy jedynką trygonometryczną.
Narysujmy dowolny trójkąt prostokątny o przyprostokątnych długości i , przeciwprostokątnej długości oraz kącie ostrym , leżącym przy boku .
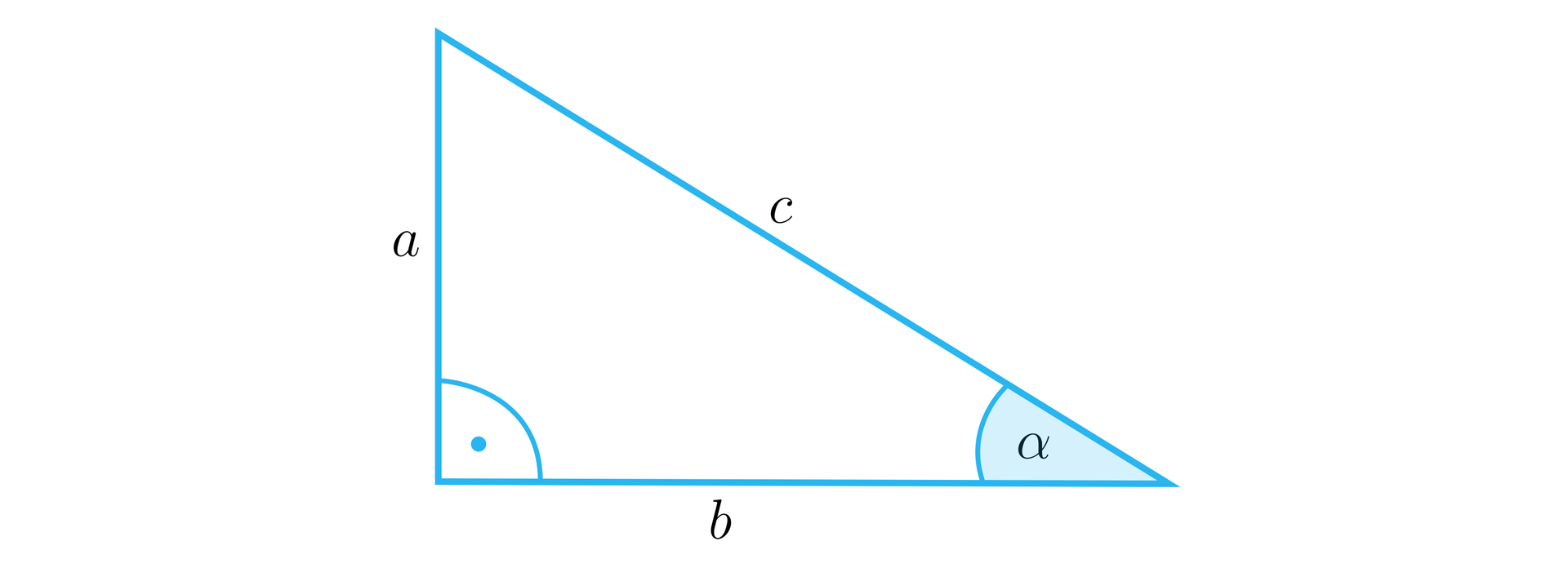
Z definicji funkcji trygonometrycznych wiadomo, że:
oraz .
Zatem:
.
Stosując równanie jedynki trygonometrycznej możemy wyznaczyć wartość sinusa kąta mając podany cosinus lub odwrotnie. Wzór ten stosujemy również dla kątów większych od .
Wyznaczymy wartość , jeżeli dany jest oraz jest kątem ostrym.
W celu wyznaczenia wartości wykorzystamy wzór .
Podstawiamy wartość .
Otrzymujemy równanie:
.
Stąd , więc lub . Ponieważ kąt jest ostry, zatem .
Dla dowolnego kąta mamy, że oraz , zaś dla zachodzą warunki: oraz .
Wyznaczymy wartość , jeżeli dany jest oraz jest kątem ostrym.
W celu wyznaczenia wartości wykorzystamy wzór .
Podstawiamy wartość .
Otrzymujemy równanie:
.
Stąd , więc lub . Ponieważ kąt jest ostry, zatem .
Sprawdzimy, czy istnieje taki kąt , dla którego oraz .
Podane wartości oraz podstawiamy do jedynki trygonometrycznej.
Otrzymujemy: .
Ponieważ , zatem nie istnieje taki kąt.
Wyznaczymy wartość oraz , jeżeli wiadomo że jest kątem ostrym oraz sinus tego kąta jest dwa razy większy od cosinusa.
Z zadania możemy ułożyć następujący warunek:
.
Podany warunek podstawiamy do jedynki trygonometrycznej. Otrzymujemy równanie:
, zatem .
Czyli , więc lub .
Ponieważ jest kątem ostrym, zatem oraz .
Wyznaczymy wartość wyrażenia , jeżeli .
Wykorzystamy wzór skróconego mnożenia na kwadrat sumy.
Zatem mamy:
.
Wiadomo, że stosunek sinusa pewnego kąta ostrego do cosinusa tego kąta wynosi . Wyznaczymy wartość wyrażenia .
Z warunku podanego w zadaniu mamy, że , zatem .
Podstawiamy to wyrażenie do jedynki trygonometrycznej i otrzymujemy: , co po przekształceniu daje .
Z równania otrzymujemy, że , więc , bo jest kątem ostrym.
Zatem .
Szukana suma wynosi .
Słownik
dla dowolnego kąta zachodzi równość