Przeczytaj

Rozważmy najpierw średnią geometryczną dwóch liczb.

Średnia geometryczna (średnia proporcjonalna) dwóch liczb

Definicja: Średnia geometryczna (średnia proporcjonalna) dwóch liczb

Średnią geometryczną dwóch liczb dodatnich $a$ i $b$ nazywamy taką liczbę dodatnią $c$ , że

\frac{a}{c} = \frac{c}{b}

Z definicji wynika, że $c^{2} = a b$ , zatem $c = \sqrt{a b}$ .

Geometrycznie możemy określić średnią geometryczną jako długość boku kwadratu, którego pole jest równe polu prostokąta o bokach długości $a$ i $b$ .

RyZ6mTCQS5Ar7

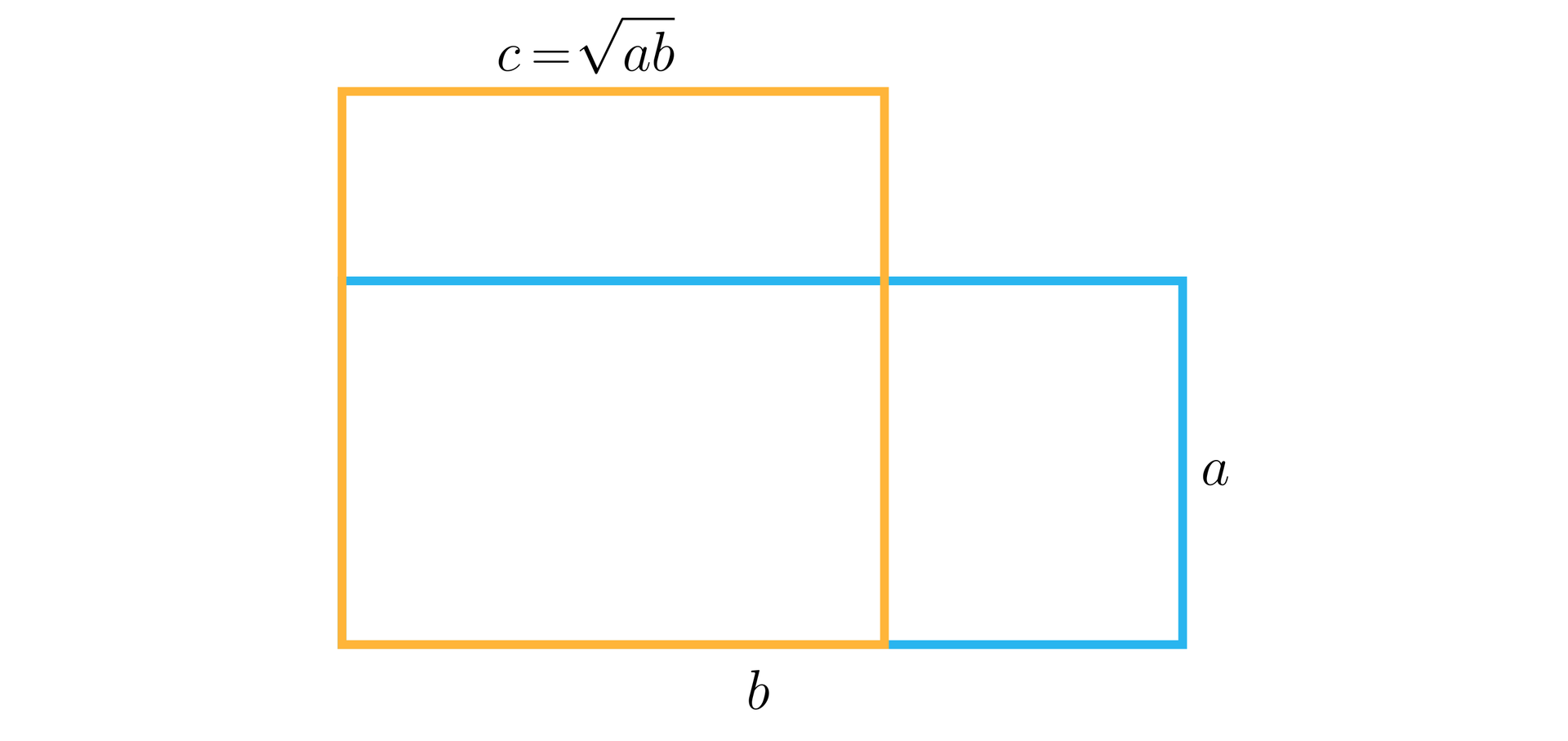
Rysunek przedstawia kwadrat i prostokąt o wspólnym lewym dolnym wierzchołku. Bok kwadratu jest krótszy niż podstawa prostokąta i jednocześnie dłuższy, niż pionowy bok prostokąta, więc w górnej części kwadrat wystaje nad prostokątem, a po prawej stronie prostokąt wystaje za kwadrat. Podstawa prostokąta to b, a jego pionowy bok to b, natomiast bok kwadratu to c=ab.

Ważne!

Często w obliczeniach, szczególnie statystycznych, średnią geometryczną oznaczamy: ${\bar{x}}_{g}$ lub $G$ .

Przykład 1

Obliczymy średnią geometrycznąśrednią geometryczną:

liczb $4$ i $16$
${\bar{x}}_{g} = \sqrt{4 \cdot 16} = \sqrt{64} = 8$ ,

liczb $2$ i $3$
${\bar{x}}_{g} = \sqrt{2 \cdot 3} = \sqrt{6}$ .

Zauważmy, że średnia geometryczna może być liczbą wymierną dodatnią, bądź niewymierną dodatnią. Nie może być zerem, ani liczbą ujemną, gdyż zakładamy, że określamy średnią geometryczną tylko dla wartości dodatnich (w przeciwieństwie np. do średniej arytmetycznej).

Definicję średniej geometrycznej można uogólnić, na przypadek $n$ liczb.

Średnia geometryczna

Definicja: Średnia geometryczna

Średnią geometryczną $n$ liczb dodatnich $a_{1}$ , $a_{2}$ , $a_{3}$ , $. . .$ , $a_{n}$ , gdzie $n = 2, 3, 4, . . .$ nazywamy liczbę

{\bar{x}}_{g} = \sqrt[n]{a_{1} \cdot a_{2} \cdot a_{3} \cdot . . . \cdot a_{n}}

W przypadku trzech liczb $a$ , $b$ , $c$ średnią geometryczną tych liczb można interpretować, jako długość krawędzi sześcianu, którego objętość jest równa objętości prostopadłościanu o długościach krawędzi $a$ , $b$ , $c$ .

Przykład 2

Obliczymy średnią geometryczną:

liczb $2$ , $2$ , $4$ , $16$
${\bar{x}}_{g} = \sqrt[4]{2 \cdot 2 \cdot 4 \cdot 16} = \sqrt[4]{256} = 4$ ,

liczb $4$ , $5$ , $6$ , $10$ , $11$ , $13$
${\bar{x}}_{g} = \sqrt[6]{4 \cdot 5 \cdot 6 \cdot 10 \cdot 11 \cdot 13} = \sqrt[6]{171600} \approx 7, 45$ .

W przypadku odliczania średniej geometrycznej dużej liczby danych, obliczanie pierwiastków wyższych stopni może sprawiać kłopot, zatem wygodniej jest korzystać wtedy z postaci zlogarytmowanej tej średniej.

Na przykład jeśli liczby $a$ , $b$ , $c$ są dodatnie i $c = \sqrt{a b}$ to

\log c = \log (\sqrt{a b})

Z własności logarytmu potęgi i logarytmu iloczynu wynika, że

\log c = \frac{\log a + \log b}{2}

Zatem logarytm przekształca zależności zapisane za pomocą iloczynu w zależności zapisane za pomocą sumy. Zauważmy też, że liczby $\log a$ , $\log b$ , $\log c$ tworzą ciąg arytmetyczny.

Średnia geometryczna danych liczb dodatnich jest zawsze nie mniejsza od średniej harmonicznej tych liczb i nie większa od ich średniej arytmetycznej.

Nierówność między średnimi

Twierdzenie: Nierówność między średnimi

Dla dodatnich liczb rzeczywistych $a_{1}$ , $a_{2}$ , $. . .$ , $a_{n}$ zachodzą następujące zależności

\frac{n}{\frac{1}{a_{1}} + \frac{1}{a_{2}} + . . . + \frac{1}{a_{n}}} \leq \sqrt[n]{a_{1} \cdot a_{2} \cdot . . . \cdot a_{n}} \leq \frac{a_{1} + a_{2} + . . . + a_{n}}{n}

Średnia geometryczna a ciąg geometryczny

Przypomnimy teraz zależność między trzema kolejnymi wyrazami ciągu geometrycznego.

Zależność między trzema kolejnymi wyrazami ciągu geometrycznego

Twierdzenie: Zależność między trzema kolejnymi wyrazami ciągu geometrycznego

Jeżeli ciąg $(a_{n})$ jest ciągiem geometrycznym o wyrazach dodatnich, to każdy wyraz tego ciągu (za wyjątkiem wyrazu pierwszego i ostatniego – w przypadku ciągu skończonego) jest średnią geometryczną wyrazów z nim sąsiadujących.

a_{n} = \sqrt{a_{n - 1} \cdot a_{n + 1}}

dla $n = \{2, 3, 4, . . .\}$ .

Powyższą zależność można uogólnić:

Jeżeli $(a_{n})$ jest ciągiem geometrycznym o wyrazach dodatnich, $a_{n}$ nie jest ani pierwszym wyrazem ciągu, ani ostatnim, to

a_{n} = \sqrt{a_{n - k} \cdot a_{n + k}}

dla $n = \{2, 3, 4, . . .\}$ , $k = \{1, 2, 3, . . .\}$ i $k < n$ .

Przykład 3

Liczby dodatnie $x + 4$ , $2 x$ , $x - \frac{1}{5}$ , w podanej kolejności, tworzą ciąg geometryczny. Znajdziemy wyrazy tego ciągu.

Liczby $x + 4$ , $2 x$ , $x - \frac{1}{5}$ są liczbami dodatnimi, czyli:

$x + 4 > 0 \Rightarrow x > - 4$ i $2 x > 0 \Rightarrow x > 0$ i $x - \frac{1}{5} > 0 \Rightarrow x > \frac{1}{5}$ .

Zatem $x > \frac{1}{5}$ .

Wiemy, że wyraz środkowy, czyli $2 x$ jest średnią geometryczną wyrazów skrajnych, czyli:

$2 x = \sqrt{(x + 4) (x - \frac{1}{5})}$

Obie strony zapisanej równości są dodatnie, więc możemy podnieść je do kwadratu i wykonać wskazane działania.

$4 x^{2} = x^{2} - \frac{1}{5} x + 4 x - \frac{4}{5}$

Otrzymane równanie kwadratowe sprowadzamy do postaci ogólnej i rozwiązujemy.

$3 x^{2} - \frac{19}{5} x + \frac{4}{5} = 0 | \cdot 5$

$15 x^{2} - 19 x + 4 = 0$

$∆ = 121$

$\sqrt{∆} = 11$

$x_{1} = \frac{19 - 11}{30} = \frac{4}{15} > \frac{1}{5}$

$x_{2} = \frac{19 + 11}{30} = 1 > \frac{1}{5}$

Obie uzyskane liczby są większe od $\frac{1}{5}$ , więc spełniają warunki zadania. Istnieją więc dwa ciągi o własnościach podanych w treści zadania.

Dla $x_{1} = \frac{4}{15}$ otrzymujemy:

$\frac{4}{15} + 4 = \frac{64}{15}$

$2 \cdot \frac{4}{15} = \frac{8}{15}$

$\frac{4}{15} - \frac{1}{5} = \frac{1}{15}$

Dla $x_{2} = 1$ otrzymujemy:

$1 + 4 = 5$

$2 \cdot 1 = 2$

$1 - \frac{1}{5} = \frac{4}{5}$

Odpowiedź:

Istnieją dwa ciągi spełniające warunki zadania: $(\frac{64}{15}, \frac{8}{15}, \frac{1}{15})$ i $(5, 2, \frac{4}{5})$ .

Przykład 4

Ciąg $(a_{1}, a_{2}, a_{3}, . . ., a_{n})$ jest ciągiem geometrycznym o wyrazach dodatnich. Wykażemy, że średnia geometryczna jego wszystkich wyrazów jest równa średniej geometrycznej wyrazu pierwszego i ostatniego.

Mamy wykazać, że $\sqrt[n]{a_{1} \cdot a_{2} \cdot a_{3} \cdot . . . \cdot a_{n}} = \sqrt{a_{1} \cdot a_{n}}$ .

Oznaczmy:
$q$ – iloraz ciągu.

Wyrazy ciągu są dodatnie, zatem $q > 0$ .

Przekształcimy każdą ze stron dowodzonej równości, zapisując wyrazy ciągu za pomocą wyrazu pierwszego i ilorazu.

Zaczniemy od lewej strony.

$L = \sqrt[n]{a_{1} \cdot a_{2} \cdot a_{3} \cdot . . . \cdot a_{n}}$

$L = \sqrt[n]{a_{1} \cdot a_{1} \cdot q \cdot a_{1} \cdot q^{2} \cdot . . . \cdot a_{1} \cdot q^{n - 1}}$

Korzystamy z własności iloczynu potęg o tych samych podstawach – wykładniki dodajemy.

$L = \sqrt[n]{{a_{1}}^{n} \cdot q^{1 + 2 + 3 + . . . + n - 1}}$

Suma $1 + 2 + 3 + . . . + n - 1$ to suma kolejnych wyrazów ciągu arytmetycznego, zatem

$1 + 2 + 3 + . . . + n - 1 = \frac{1 + n - 1}{2} \cdot (n - 1) = \frac{n (n - 1)}{2}$

Otrzymujemy:

$L = \sqrt[n]{{a_{1}}^{n} \cdot q^{\frac{n (n - 1)}{2}}}$

Liczby $a_{1}$ i $q$ są dodatnie, więc

$L = a_{1} \cdot q^{\frac{n - 1}{2}}$

Teraz pora na przekształcenie prawej strony dowodzonej równości.

$P = \sqrt{a_{1} \cdot a_{n}}$

$P = \sqrt{a_{1} \cdot a_{1} \cdot q^{n - 1}}$

$P = \sqrt{{a_{1}}^{2} \cdot q^{n - 1}}$

Zapisując pierwiastek w postaci potęgi o wykładniku ułamkowych, otrzymujemy

$P = {({a_{1}}^{2} \cdot q^{n - 1})}^{\frac{1}{2}}$

$P = a_{1} \cdot q^{\frac{n - 1}{2}}$

Zatem:

$P = L$ , co kończy dowód.

Średnia geometryczna w statystyce

W statystyce średnia geometryczna znajduje zastosowanie przy badaniu średniego tempa zmian zjawisk, gdy zjawiska zmieniają się w ujęciu dynamicznym. Średnia geometryczna mówi o wzroście lub spadku wartości danej zmiennej w badanym okresie, co jest szczególnie przydatne przy analizie wyników inwestycyjnych. Średnią geometryczną często wtedy wyrażamy w procentach.

Przykład 5

Pan Kowalski zainwestował kwotę $100 zł$ . W trzech kolejnych latach kapitał zainwestowany osiągnął następujące wartości: $80 zł$ na koniec pierwszego roku, $50 zł$ na koniec drugiego roku, $90 zł$ na koniec trzeciego roku. Obliczymy średnią stopę zwrotu zainwestowanego kapitału na koniec rozważanego okresu.

Stopa zwrotu to wyrażony w procentach zwrot osiągnięty z inwestycji w danym roku w relacji do jej kosztu.

Aby obliczyć, czy inwestycja przynosi zysk czy straty w dłuższym okresie czasu, obliczamy średnią geometryczną tzw. indeksów. Indeks to miernik, który porządkuje wyniki pewnej liczby szczegółowych obserwacji, charakteryzuje zmiany w czasie. Indeks obliczymy jako iloraz kapitału w okresie $n$ przez kapitał w okresie $n - 1$ .

Obliczenia zapiszemy w tabelce.

Okres	Wartość kapitału	Indeks
$0$	$100$	$-$
$1$	$80$	$\frac{80}{100} = 0, 8$
$2$	$50$	$\frac{50}{80} = 0, 625$
$3$	$90$	$\frac{90}{50} = 1, 8$
Iloczyn indeksów		$0, 8 \cdot 0, 625 \cdot 1, 8 = 0, 9$
Średnia geometryczna indeksów		$\sqrt[3]{0, 9} \approx 0, 9655$
Średnia stopa zwrotu (średnia geometryczna indeksów $- 1$ )		$0, 9655 - 1 = - 0, 0345$
Średnia stopa zwrotu wyrażona w procentach		$- 3, 45 %$

Odpowiedź:

Średnia stopa zwrotu to około $(- 3, 45 %)$ .

Przykład 6

W tabelce przedstawione są dane na temat liczby posiadanych samochodów przez mieszkańców pewnego miasta, w latach $2017 - 2020$ .

Rok	Liczba samochodów
$2017$	$345010$
$2018$	$328000$
$2019$	$426800$
$2020$	$401364$

Ustalimy średnie tempo zmian liczby samochodów w badanym okresie.

Najpierw ustalamy tempo zmian w dwóch kolejnych latach.

$\frac{328000}{345010} \approx 0, 95$

$\frac{426800}{328000} \approx 1, 30$

$\frac{401364}{426800} \approx 0, 94$

Wyznaczamy średnią geometryczną znalezionych liczb.

${\bar{x}}_{g} = \sqrt[3]{0, 95 \cdot 1, 30 \cdot 0, 94} \approx 1, 05$

W badanym okresie średni przyrost liczby samochodów wyniósł $(1, 05 - 1) \cdot 100 % = 5 %$ .

Zastosowanie geometryczne średniej geometrycznej

W wielu problemach geometrycznych pojawiają się zagadnienia, których rozwiązanie prowadzi do uzyskania średniej geometrycznej. Średnia geometryczna jest istotą złotego podziału, wykorzystuje się ją do przybliżonej konstrukcji kwadratury koła, czy konstrukcji siedemnastokąta foremnego.

Przykład 7

Przekątne trapezu $A B C D$ przecinają się w punkcie $E$ i dzielą trapez na cztery trójkąty takie, że $P_{△ A E D} = P_{△ B E C}$ (patrz rysunek). Można udowodnić, że $P_{△ A E D} = \sqrt{P_{△ A B E} \cdot P_{△ C D E}}$ .
R27230ofMkuhH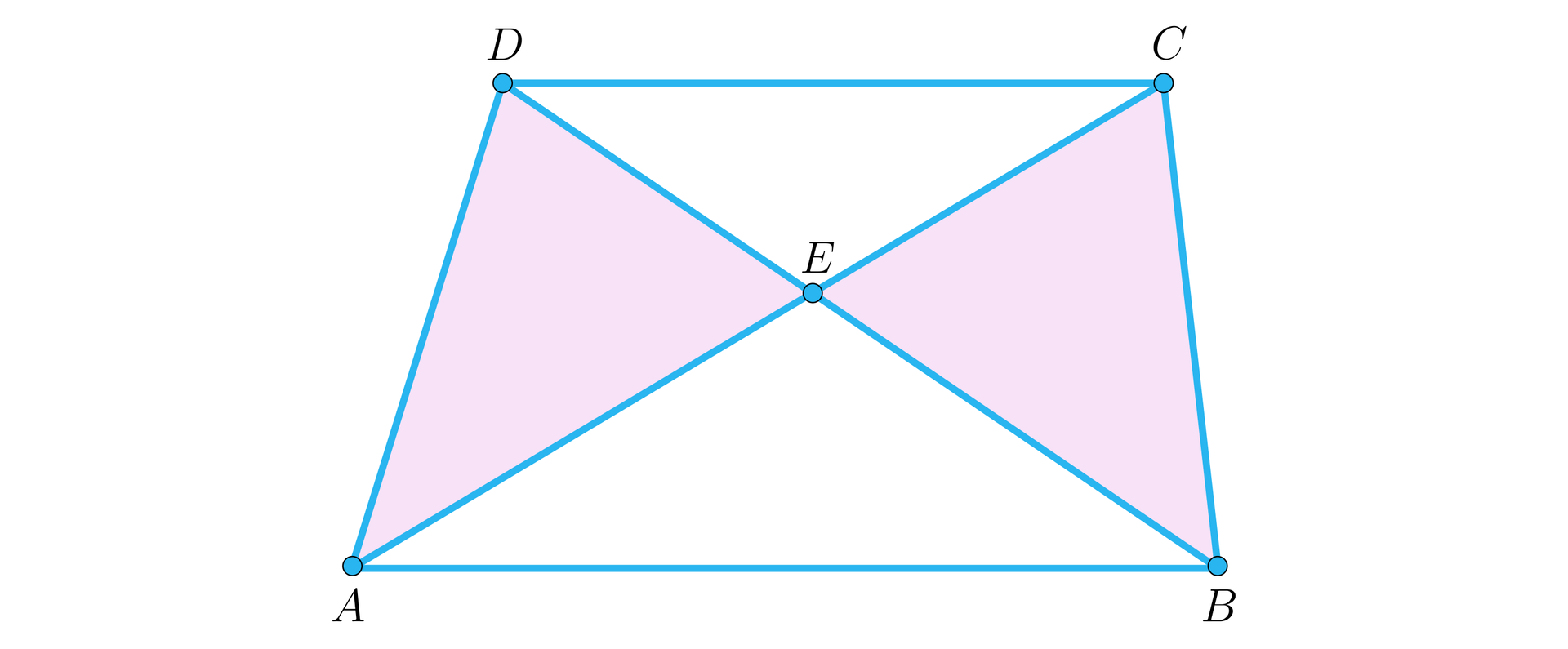

Jeżeli w trójkątach $A B D$ i $B C E$ boki $A D$ i $B E$ są równoległe oraz boki $B D$ i $C E$ są równoległe (patrz rysunek), to $P_{△ B E D} = \sqrt{P_{△ A B D} \cdot P_{△ B C E}}$ .
Rez681k5gLtRh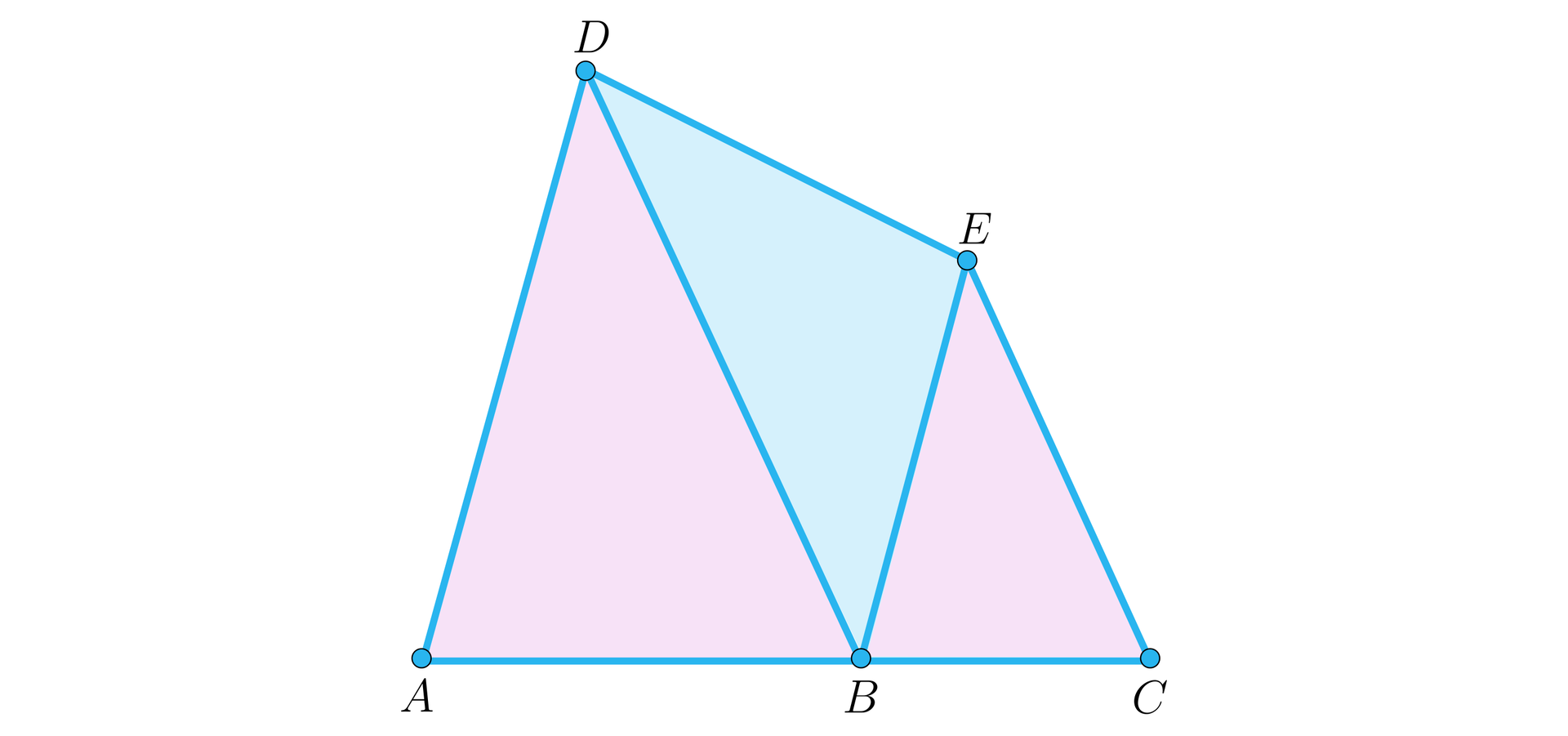
Rysunek przedstawia trzy trójkąty o wybranych wspólnych wierzchołkach. Po lewo mamy trójkąt $A B D$ . Dodajmy, że wierzchołek $A$ leży po lewej stronie, wierzchołek $B$ po prawej oraz wierzchołek $D$ w górnej części. Trójkąt ten ma wspólny jeden wierzchołek z trójkątem $B C E$ , którego wierzchołki rozkładają się następująco: wierzchołek $B$ leży po lewej stronie, wierzchołek $C$ po prawej oraz wierzchołek $E$ w górnej części. Oba trójkąty wyróżniono różowym tłem. Między nimi na niebiesko wyróżniono trzeci trójkąt $D B E$ , którego wierzchołki rozkładają się następująco: wierzchołek $D$ leży po lewej stronie w górnej części, wierzchołek $B$ znajduje się w dolnej środkowej części, a po prawej stronie w górnej część leży wierzchołek $E$ .

Przykład 8

Dane są odcinki o długościach $a$ i $b$ . Skonstruujemy odcinek $c$ , którego długość jest średnią geometryczną długości tych odcinków.

Rysujemy prostą, na której odkładamy odcinki $|O A| = a$ i $|A B| = b$ .

Kreślimy półokrąg o średnicy $O B$ .

Przez punkt $A$ prowadzimy prostą prostopadłą do prostej $O B$ .

Prosta ta przecina półokrąg w punkcie $C$ .

Odcinek $|C A| = \sqrt{a b} = c$ .

RkHq4WswltmXe

Rysunek przedstawia trójkąt OBC, w którym odcinek OB jest poziomą podstawą. Z wierzchołka C poprowadzono wysokość opisaną jako ab do punktu A, która podzieliła podstawę na dwie części: lewą a będącą odcinkiem OA oraz prawą b będącą odcinkiem AB. Z punktu O do punktu B poprowadzono na zewnątrz trójkąta półokrąg. Wewnątrz obu trójkątów zaznaczono kąty za pomocą mały łuków narysowanych między wyznaczającymi je ramionami.

Poprawność tej konstrukcji wynika z podobieństwa trójkątów $O B C$ , $O A C$ i $C A B$ .

W trójkącie $O B C$ kąt $O C B$ jest prosty (jako kąt oparty na półokręgu), trójkąty $O A C$ i $C A B$ są również prostokątne i ich kąty ostre są odpowiednio równe.

Zatem:

$\frac{|C A|}{a} = \frac{b}{|C A|}$

${|C A|}^{2} = a b$

$|C A| = \sqrt{a b}$ .

Przykład 9

Okrąg o środku $O_{1}$ i średnicy $a$ jest styczny zewnętrznie do okręgu o środku $O_{2}$ i średnicy $b$ , przy czym $a > b$ . Prosta $p$ jest wspólną styczną do tych okręgów, odpowiednio w punktach $A$ i $B$ . Wykażemy, że $|A B| = \sqrt{a b}$ .

R5B85fTZ4hFYz

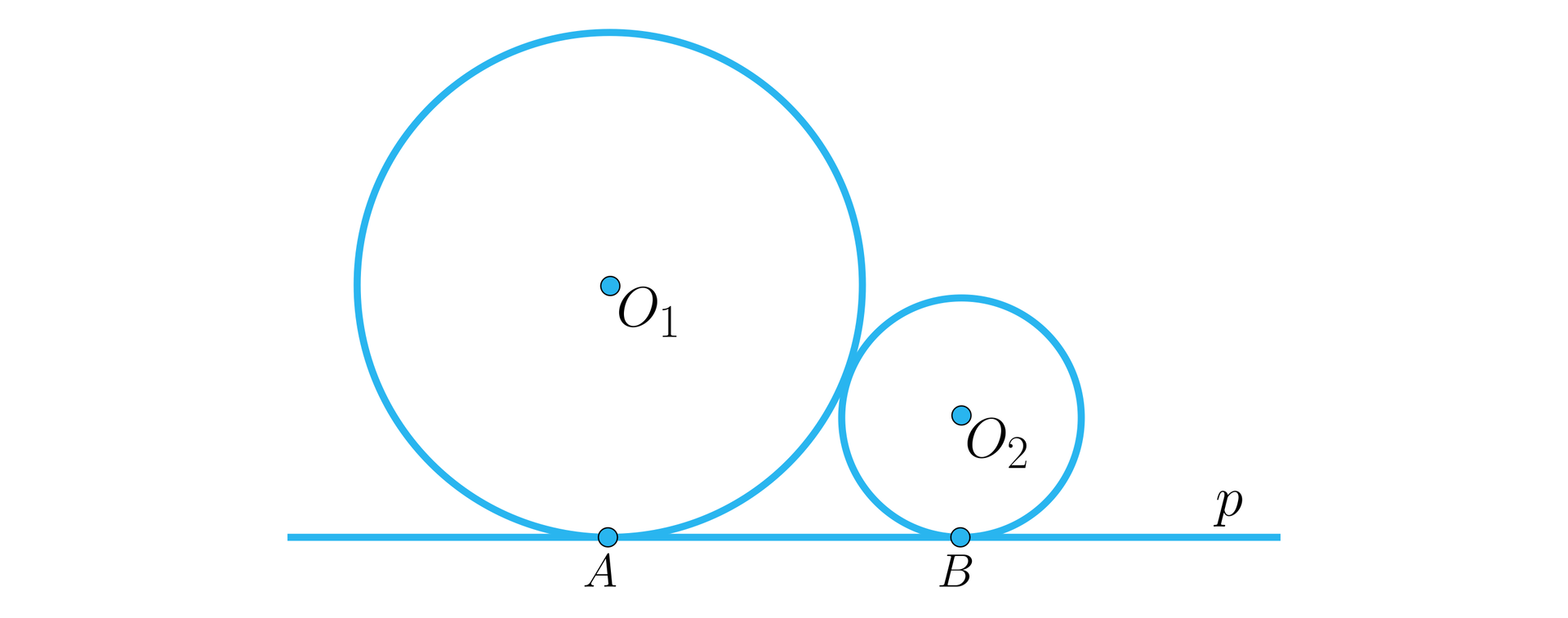
Rysunek przestawia poziomą prostą p, na której oparto dwa okręgi: lewy większy o środku w punkcie O1, którego punkt styczności z prostą to punkt A oraz lewy, mniejszy okrąg o środku w punkcie O2, którego punkt styczności z prostą to punkt B.

Rozwiązanie:

Ze środków danych okręgów poprowadźmy promienie do punktów styczności. Utworzone w ten sposób odcinki $|O_{1} A| = \frac{a}{2}$ i $| O_{2} B | = \frac{b}{2}$ są prostopadłe do prostej $p$ (promień w punkcie styczności jest prostopadły do stycznej), są więc równoległe.

Utwórzmy trójkąt $O_{1} C O_{2}$ o boku $C O_{2}$ równoległym do prostej $p$ i taki, że punkt $C$ należy do $O_{1} A$ .

Trójkąt ten jest trójkątem prostokątnym, w którym przyprostokątna $|O_{1} C| = \frac{a - b}{2}$ i przeciwprostokątna $|O_{1} O_{2}| = \frac{a + b}{2}$ .

RMcjVzjolYOV6

Korzystając z twierdzenia Pitagorasa, obliczamy długość przyprostokątnej $C O_{2}$ .

${(\frac{a - b}{2})}^{2} + {|C O_{2}|}^{2} = {(\frac{a + b}{2})}^{2}$

Po przekształceniach otrzymujemy:

$4 {|C O_{2}|}^{2} = (a^{2} + 2 a b + b^{2}) - (a^{2} - 2 a b + b^{2})$

$4 {|C O_{2}|}^{2} = 4 a b$

${|C O_{2}|}^{2} = a b$

Ponieważ $a > 0$ , $b > 0$ , jako promienie okręgów, stąd

$|C O_{2}| = \sqrt{a b}$ .

Słownik

średnia geometryczna (średnia proporcjonalna) dwóch liczb

średnią geometryczną dwóch liczb dodatnich $a$ i $b$ nazywamy taką liczbę dodatnią $c$ , że

\frac{a}{c} = \frac{c}{b}

Wprowadzenie

Infografika

Średnia geometryczna a ciąg geometryczny

Średnia geometryczna w statystyce

Zastosowanie geometryczne średniej geometrycznej

Słownik