Przeczytaj

Przypomnijmy algorytm rozkładania liczby naturalnej na czynniki pierwsze:

Po prawej stronie rozważanej liczby naturalnej $n$ stawiamy pionową kreskę.
Szukamy jakiejkolwiek liczby pierwszej $p_{1}$ , która dzieli daną liczbę – zapisujemy ją po prawej stronie kreski na wysokości liczby $n$ .
Dzielimy liczbę $n$ przez liczbę $p_{1}$ – wynik $n_{1}$ tego dzielenia zapisujemy po lewej stronie kreski pod liczbą $n$ .
Czynności 2) i 3) powtarzamy dla liczby $n_{1}$ – liczbę pierwszą $p_{2}$ dzielącą liczbę $n_{1}$ zapisujemy pod liczbą $p_{1}$ . Wynik $n_{2}$ tego dzielenia zapisujemy pod liczbą $n_{1}$ .
Algorytm kontynuujemy, aż po lewej stronie kreski pojawi się liczba $1$ .

RrCj0La98O2r4

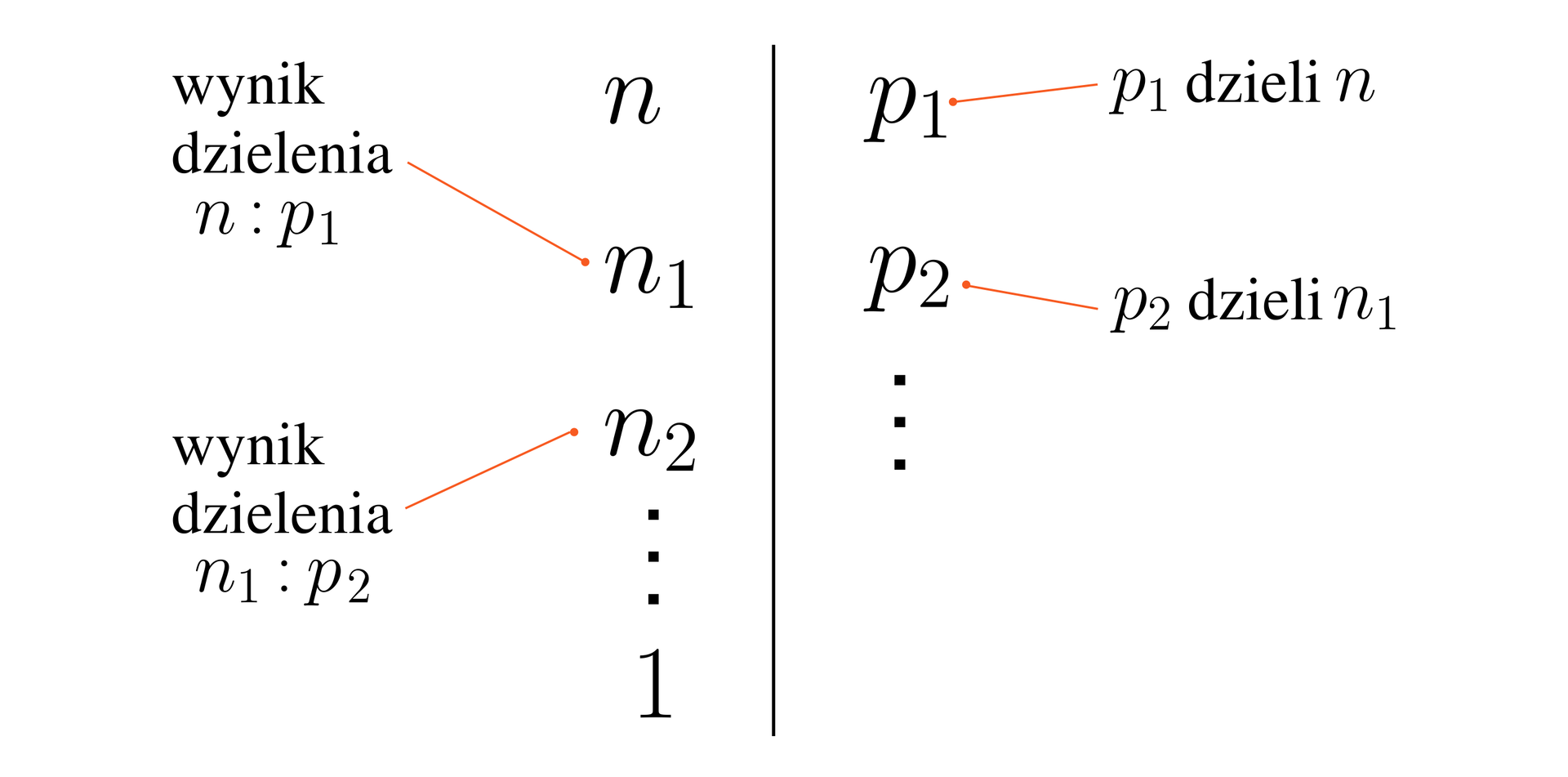
Na ilustracji przedstawiono dwa pionowe rzędy czynników oddzielone prostą. Po lewej stronie prostej zapisano, kolejno od góry n, n1, n2. Po prawej stronie prostej, równolegle do n, czynnik p1 oraz równoległe do n1 czynnik p2. Najbardziej po lewej umieszczono następujące napisy. Wynik dzielenia n÷p1, od którego poprowadzono strzałkę do n1 oraz wynik dzielenia n1÷p2, od którego poprowadzono strzałkę do n2. Najbardziej po prawej umieszczono napisy. p1 dzieli n, od którego poprowadzono strzałkę do p1 oraz p2 dzieli n1 od którego poprowadzono strzałkę do p2.

Wobec powyższego $n = p_{1} \cdot p_{2} \cdot \dots \cdot p_{k}$ .

Przykład 1

Przedstawmy liczbę $360$ w postaci iloczynu czynników pierwszych.

Zauważmy przy okazji, że kolejność znajdowania czynników pierwszych nie ma znaczenia – efekt jest taki sam, chociaż przyjęło się, że zaczynamy dzielenie od najmniejszych liczb pierwszych.

RQYTXAmD84UdV

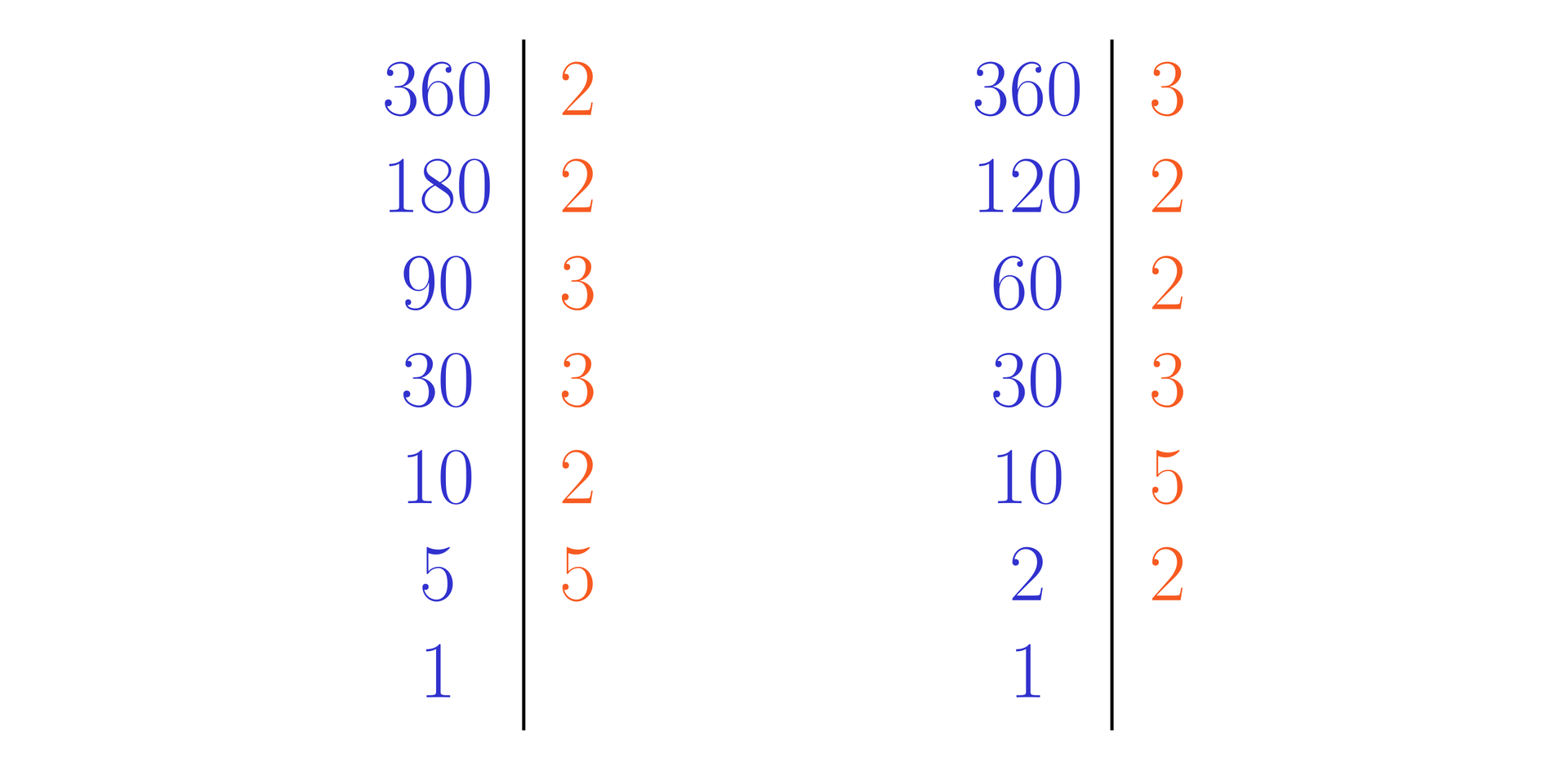
Na ilustracji przedstawiono dwa sposoby przedstawienia liczby 360 w postaci iloczynu czynników pierwszych. Sposób 1. Przedstawiono dwa pionowe rzędy liczb oddzielone prostą. Po lewej stronie prostej zapisano kolejno od góry 360, 180, 90, 30, 10, 5 oraz jeden. Po prawej stronie zapisano kolejno od góry 2, 2, 3, 3, 2 oraz pięć. Sposób 2. Przedstawiono dwa pionowe rzędy liczb oddzielone prostą. Po lewej stronie zapisano kolejno od góry 360, 120, 60, 30, 10, 2 oraz jeden. Po prawej stronie zapisano kolejno od góry 3, 2, 2, 3, 5 oraz 2.

Zatem możemy zapisać $360 = 2^{3} \cdot 3^{2} \cdot 5$ .

Zauważmy, że każdy dzielnik liczby 360 jest pewną kombinacją jego dzielników pierwszych.

Na przykład liczba $360$ dzieli się przez $8$ (bo $8 = 2 \cdot 2 \cdot 2$ ), ale nie przez $16$ (bo $16 = 2 \cdot 2 \cdot 2 \cdot 2$ ), $360$ dzieli się przez $45$ (bo $45 = 3 \cdot 3 \cdot 5$ ), ale nie przez $135$ (bo $135 = 3 \cdot 3 \cdot 3 \cdot 5$ ). Liczba $360$ nie dzieli się też przez $13$ , ani przez $26$ (bo $26 = 2 \cdot 13$ ).

Zatem każdy dzielnik $d$ liczby $360$ jest postaci $d = 2^{w_{1}} \cdot 3^{w_{2}} \cdot 5^{w_{3}}$ , przy czym $w_{1} \in \{0, 1, 2, 3\}$ , $w_{2} \in \{0, 1, 2\}$ , $w_{3} \in \{0, 1\}$ .

RWWd60vETMRiq

Na ilustracji przedstawiono tabelę składającą się z trzech kolumn. Pierwszą kolumnę od lewej zatytułowano potęga liczba dwa. Kolejno od góry wypisano liczby dwa do potęgi zerowej, dwa do potęgi pierwszej, dwa do potęgi drugiej oraz dwa do potęgi trzeciej. Środkową kolumnę zatytułowano potęga liczby trzy. Kolejno od góry wypisano liczby, trzy do potęgi zerowej, trzy do potęgi pierwszej oraz trzy do potęgi drugiej. Trzecią kolumnę zatytułowano potęga liczby pięć. Kolejno od góry wypisano liczby, pięć do potęgi zerowej oraz pięć do potęgi pierwszej. Liczby w poszczególnych kolumnach połączono strzałkami w odpowiedniej kolejności, z których powstały następujące równania 22×32×50=36, 20×31×51=15, 23×30×51=40.

Ponieważ tworząc dzielnik $d$ liczby $360$ możemy użyć dowolnej spośród potęg liczby $2$ o wykładniku $0$ , $1$ , $2$ , $3$ (co daje $4$ możliwości), dowolnej spośród potęg liczby $3$ o wykładniku $0$ , $1$ , $2$ (co daje $3$ możliwości) oraz dowolnej spośród potęg liczby $5$ o wykładniku $0$ , $1$ (co daje $2$ możliwości), to wszystkich dzielników liczby $360$ jest $4 \cdot 3 \cdot 2 = 24$ . Zauważmy jeszcze, że $1 = 2^{0} \cdot 3^{0} \cdot 5^{0}$ .

Ogólnie jeśli liczba naturalna $x$ przedstawia się jako iloczyn liczb pierwszych w następujący sposób

{p_{1}}^{k_{1}} \cdot {p_{2}}^{k_{2}} \cdot {p_{3}}^{k_{3}} \cdot . . . \cdot {p_{n}}^{k_{n}}

to każdy jej dzielnik $d$ jest postaci:

{p_{1}}^{w_{1}} \cdot {p_{2}}^{w_{2}} \cdot {p_{3}}^{w_{3}} \cdot . . . \cdot {p_{n}}^{w_{n}}

gdzie:
$w_{1} \in \{0, 1, 2, . . ., k_{1}\}$ , $w_{2} \in \{0, 1, 2, . . ., k_{2}\}$ , $w_{3} \in \{0, 1, 2, . . ., k_{3}\}$ , $. . .$ , $w_{n} \in \{0, 1, 2, . . ., k_{n}\}$ .

Wszystkich dzielników liczby

{p_{1}}^{k_{1}} \cdot {p_{2}}^{k_{2}} \cdot {p_{3}}^{k_{3}} \cdot . . . \cdot {p_{n}}^{k_{n}}

jest

(k_{1} + 1) \cdot (k_{2} + 1) \cdot (k_{3} + 1) \cdot . . . \cdot (k_{n} + 1)

Przykład 2

Wyznaczymy liczbę wszystkich dzielników liczb

a) $100$

b) $600$

a) Każdy dzielnik liczby $100 = 2^{2} \cdot 5^{2}$ ma swoim rozkładzie na czynniki pierwszerozkład na czynniki pierwszerozkładzie na czynniki pierwsze tylko i wyłącznie zerową, pierwszą lub drugą potęgę liczby $2$ oraz zerową, pierwszą lub drugą potęgę liczby $5$ . Czyli dzielnik liczby $100$ może zawierać jedynie jedną z trzech potęg liczby $2$ ( $1$ , $2$ lub $4$ ) oraz jedną z trzech potęg liczby $5$ ( $1$ , $5$ lub $25$ ). Zatem wszystkich dzielników liczby $100$ jest $3 \cdot 3 = 9$ . Wypiszmy je wszystkie:

R1RLkZMazQisC

Na ilustracji przedstawiono przykład, zobrazowany za pomocą diagramu drzewa. W rzędzie pierwszym umieszczono, kolejno od góry liczby 2 do potęgi zerowej, 2 do potęgi pierwszej oraz 2 do potęgi drugiej. Od każdej liczby odchodzą trzy strzałki do cyfr 5 do potęgi zerowej, 5 do potęgi pierwszej oraz 5 do potęgi drugiej. Od każdej potęgi liczby pięć, dla odpowiadającej jej potęgi liczby dwa, poprowadzono strzałki oraz zapisano równania. Dla potęgi 2 do zerowej 20×50=1, 20×51=5 oraz 20×52=25. Następnie dla potęgi liczby 2 do pierwszej. 21×50=2, 21×51=10 oraz 21×52=50. Dla potęgi liczby 2 do drugiej. 22×50=50, 22×51=20 oraz 22×52=100.

b) Dzielniki $d$ liczby $600 = 2^{3} \cdot 5^{2} \cdot 3$ są postaci

$d = 2^{w_{1}} \cdot 5^{w_{2}} \cdot 3^{w_{3}}$

gdzie:
$w_{1} \in \{0, 1, 2, 3\}$ , $w_{2} \in \{0, 1, 2\}$ , $w_{3} \in \{0, 1\}$ .

Zatem tworząc dzielnik liczby $600$ możemy użyć jednej z czterech potęg liczby $2$ , jednej z trzech potęg liczby $5$ oraz jednej z dwóch potęg liczby $3$ , co daje $4 \cdot 3 \cdot 2 = 24$ dzielniki.

Podsumujmy dotychczasowe rozważania w postaci twierdzenia.

Zasadnicze twierdzenie arytmetyki

Twierdzenie: Zasadnicze twierdzenie arytmetyki

Każda liczba naturalna większa od $1$ albo jest liczbą pierwszą, albo można ją jednoznacznie przedstawić w postaci iloczynu liczb pierwszych.

Jednoznaczność oznacza, że jeśli dana liczba jest przedstawiona jako iloczyn pewnych liczb pierwszych na dwa sposoby, to oba te iloczyny zawierają te same czynniki, a różnią się jedynie ich kolejnością.

Przedstawienie liczby w postaci iloczynu nazywamy rozkładem na czynniki lub faktoryzacją. Często pod pojęciem faktoryzacjifaktoryzacjafaktoryzacji rozumiemy rozkład na czynnikirozkład na czynniki pierwszerozkład na czynniki nierozkładalne, czyli w przypadku liczb – na czynniki będące liczbami pierwszymi, czasami jednak nazywamy tak dowolne przedstawienie danego obiektu matematycznego w postaci iloczynu. Znaczenie rozpoznajemy na podstawie kontekstu.

Słownik

rozkład na czynniki pierwsze

przedstawienie liczby naturalnej w postaci iloczynu liczb pierwszych; zapis zwykle zawiera naturalne potęgi liczb pierwszych

faktoryzacja

1) czynność prowadząca do przedstawienia liczby lub wyrażenia algebraicznego w postaci nietrywialnych (w przypadku liczb – różnych od $1$ ) czynników;
2) przedstawienie liczby lub wyrażenia w postaci iloczynu nietrywialnych (w przypadku liczb – różnych od $1$ ) czynników

Wprowadzenie

Animacja

Słownik