Przeczytaj

W materiale “Dzielniki i wielokrotności” przyjęliśmy następującą definicję:

Wielokrotność liczby naturalnej

n

Definicja: Wielokrotność liczby naturalnej

n

Wielokrotnością liczby naturalnej $n$ nazywamy każdy iloczyn $n$ przez dowolną liczbę naturalną.

Przykład 1

Wprost z definicji wynika, że wielokrotnościami liczby $6$ są liczby: $0$ , $6$ , $12$ , $18$ , $24$ , $30$ , $36$ , $42$ , $. . .$

Zaś wielokrotnościami liczby $4$ są liczby: $0$ , $4$ , $8$ , $12$ , $16$ , $20$ , $24$ , $28$ , $32$ , $36$ , $40$ , $. . .$

Wspólnymi wielokrotnościami liczb $6$ i $4$ są liczby: $0$ , $12$ , $24$ , $36$ , $. . .$

Najmniejszą wspólną wielokrotnością liczb $6$ i $4$ jest $0$ .

Najmniejszą dodatnią wspólną wielokrotnością liczb $6$ i $4$ jest $12$ .

Najmniejsza wspólna wielokrotność dodatnich liczb naturalnych

a

b

Definicja: Najmniejsza wspólna wielokrotność dodatnich liczb naturalnych

a

b

Najmniejszą wspólną wielokrotnością dodatnich liczb naturalnych $a$ i $b$ jest najmniejsza dodatnia liczba naturalna, która jest podzielna przez każdą z liczb $a$ i $b$ .

Analogiczną definicję można sformułować dla więcej niż dwóch liczb naturalnych.

Najmniejsza wspólna wielokrotność dodatnich liczb naturalnych

Definicja: Najmniejsza wspólna wielokrotność dodatnich liczb naturalnych

Najmniejszą wspólną wielokrotność dodatnich liczb naturalnych $a$ i $b$ oznaczamy $N W W (a, b)$ .

Wyznaczanie najmniejszej wspólnej wielokrotności metodą pokazaną w przykładzie 1 może być uciążliwe. Dlatego zwykle wykorzystujemy w tym celu rozkłady na czynniki pierwsze.

Przykład 2

Rozważymy kilka przykładów:

$N W W (2, 5) = 2 \cdot 5 = 10$ , bo $10$ to najmniejsza liczba podzielna przez $2$ i $5$ .

$N W W (2, 5, 3) = 2 \cdot 5 \cdot 3 = 30$ , bo $30$ to najmniejsza liczba podzielna przez $2$ , $5$ i $3$ .

$N W W (2^{3}, 5^{2}) = 2^{3} \cdot 5^{2} = 200$ , bo $200$ to najmniejsza liczba podzielna przez $2^{3}$ i $5^{2}$ .

$N W W (2^{3} \cdot 5^{4}, 2^{4} \cdot 5^{2}) = 2^{4} \cdot 5^{4} = 10000$ , bo $10000$ to najmniejsza liczba podzielna przez $2^{3} \cdot 5^{4}$ i $2^{4} \cdot 5^{2}$ .

$N W W (2^{3} \cdot 5^{4} \cdot 7^{2}, 2^{4} \cdot 3^{2} \cdot 5^{2}) = 2^{4} \cdot 5^{4} \cdot 7^{2} \cdot 3^{2}$ , bo $2^{4} \cdot 5^{4} \cdot 7^{2} \cdot 3^{2}$ to najmniejsza liczba podzielna przez $2^{3} \cdot 5^{4} \cdot 7^{2}$ i $2^{4} \cdot 3^{2} \cdot 5^{2}$ .

Zwróć uwagę, że rozkład na czynniki pierwsze najmniejszej wspólnej wielokrotności liczb $a$ i $b$ zawiera tylko i wyłącznie liczby pierwsze pochodzące z rozkładów liczb $a$ i $b$ .

Ponadto najmniejsza wspólna wielokrotnośćnajmniejsza wspólna wielokrotnośćnajmniejsza wspólna wielokrotność liczb, które są względnie pierwsze, jest równa ich iloczynowi.

Przykład 3

Wyznaczymy najmniejszą wspólną wielokrotność liczb $2250$ i $945$ .

Zaczniemy od rozkładu obu liczb na czynniki pierwsze:

R1LV96WLZaTlG

Ilustracja przedstawia dwa przykłady rozkładu liczby na czynniki pierwsze: liczba dwa tysiące dwieście pięćdziesiąt: podzielić przez dwa daje tysiąc sto dwadzieścia pięć podzielić przez trzy daje trzysta siedemdzieisiąt pięć podzielić przez trzy daje sto dwadzieścia pięć podzielić przez pięć daje dwadzieścia pięć podzielić przez pięć daje pięć podzielić przez pięć daje jeden. Liczba dziewięćset czterdzieści pięć podzielić przez trzy daje trzysta piętnaście podzielić przez trzy daje sto pięć podzielić przez trzy daje trzydzieści pięć podzielić przez pięć daje siedem podzielić przez siedem daje jeden.

Zatem $2250 = 2 \cdot 3^{2} \cdot 5^{3}$ oraz $945 = 3^{3} \cdot 5 \cdot 7$ .

Aby liczba dzieliła się przez $2250$ , musi dzielić się przez $2$ , drugą potęgę liczby $3$ i trzecią potęgę liczby $5$ .

Aby liczba dzieliła się przez $945$ , musi dzielić się przez $5$ , $7$ i trzecią potęgę liczby $3$ .

Najmniejsza liczba podzielna przez $2250$ i $945$ to $2 \cdot 3^{3} \cdot 5^{3} \cdot 7 = 47250$ .

Zatem $N W W (2250, 945) = 47250$ .

Zauważmy, że aby wyznaczyć najmniejszą wspólną wielokrotność dwóch liczb, wystarczy rozłożyć obie na czynniki pierwsze, a następnie pomnożyć wszystkie czynniki tworzące rozkład jednej z rozważanych liczb przez te czynniki z rozkładu drugiej, których brakuje w rozkładzie tej pierwszej.

Przykład 4

Wyznaczymy najmniejszą wspólną wielokrotność liczb $18$ , $75$ oraz $35$ .

Zauważmy, że:

R1DQrCfGzGWvv

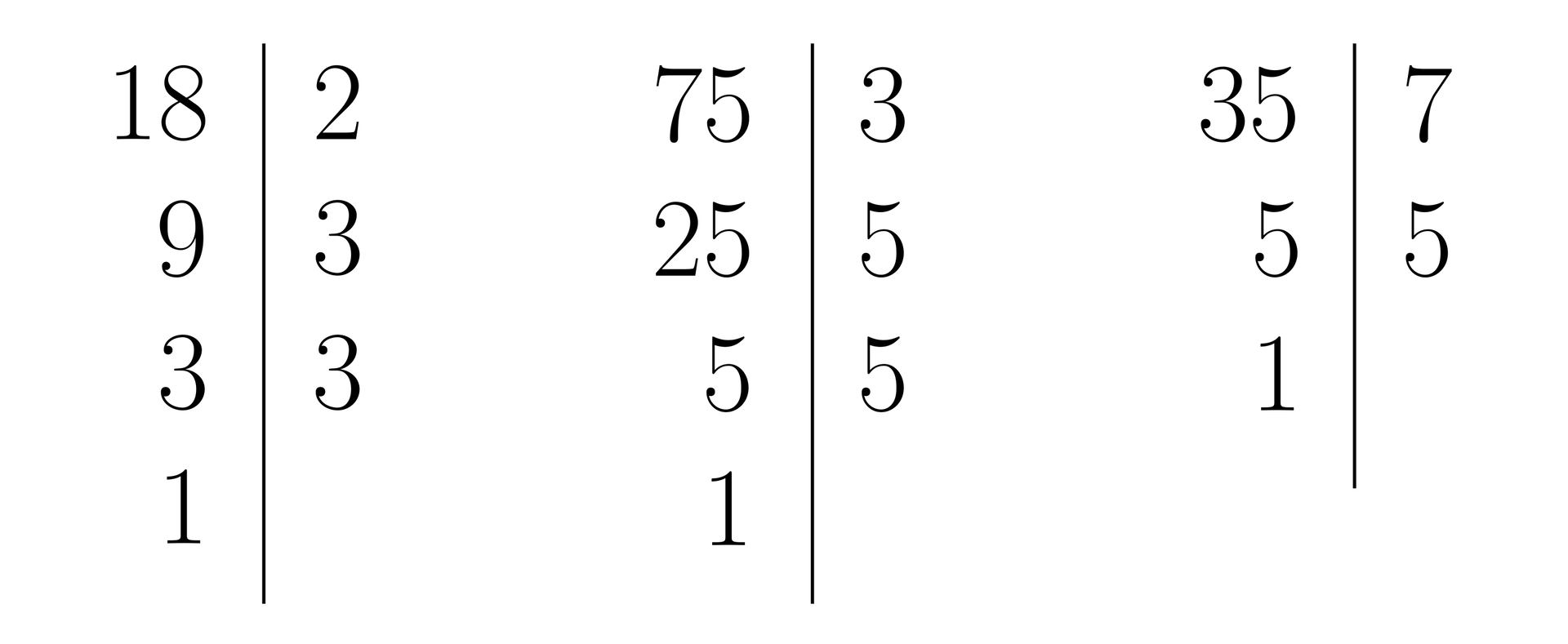
Ilustracja przedstawia trzy przykłady rozkładu liczby na czynniki pierwsze: liczba osiemnaście podzielić przez dwa daje dziewięć podzielić przez trzy daje trzy podzielić przez trzy daje jeden. Liczba siedemdziesią pięć podzielić przez trzy daje dwadzieścia pięć podzielić przez pięć daje pięć podzielić przez pięć daje jeden. Liczba trzydzieści pięć podzielić przez siedem daje pięć podzielić przez pięć daje jeden.

Aby liczba dzieliła się przez $18$ , musi dzielić się przez $2$ i drugą potęgę liczby $3$ .

Aby liczba dzieliła się przez $75$ , musi dzielić się przez $3$ i drugą potęgę liczby $5$ .

Aby liczba dzieliła się przez $35$ , musi dzielić się przez $7$ i $5$ .

Najmniejsza liczba podzielna przez $18$ , $75$ i $35$ to iloczyn liczby $2$ , drugiej potęgi liczby $3$ , drugiej potęgi liczby $5$ i liczby $7$ .

Zatem $N W W (18, 75, 35) = 2 \cdot 3^{2} \cdot 5^{2} \cdot 7 = 3150$ .

Rozważmy liczby naturalne dodatnie $a$ i $b$ . Każdą z nich można zapisać jako iloczyn ich największego wspólnego dzielnika oraz pewnej liczby naturalnej.

Zatem: $a = k \cdot d$ i $b = m \cdot d$

gdzie:
$k$ i $m$ – są liczbami naturalnymi, zaś $d = N W D (a, b)$ .

Zauważmy, że liczby $k$ i $m$ są względnie pierwsze (bo gdyby $k$ i $m$ miały dzielnik $p$ większy od $1$ , to wówczas $N W D (a, b) = d \cdot p > d$ ).

Wynika stąd, że $N W W (a, b) = k \cdot d \cdot m$ . Jeśli pomnożymy obie strony powyższej równości przez $d$ , otrzymujemy $d \cdot N W W (a, b) = k \cdot d \cdot m \cdot d$ , czyli $N W D (a, b) \cdot N W W (a, b) = a \cdot b$ .

Bardzo często stosowaną praktyką jest wyznaczanie największego wspólnego dzielnikanajwiększy wspólny dzielniknajwiększego wspólnego dzielnika dwóch liczb za pomocą algorytmu Euklidesa, a następnie obliczanie najmniejszej wspólnej wielokrotności z przekształconej postaci ostatniej równości:

N W W (a, b) = \frac{a \cdot b}{N W D (a, b)}

Przykład 5

Obliczymy $N W W (225, 420)$ korzystając ze wzoru $N W W (a, b) = \frac{a \cdot b}{N W D (a, b)}$ .

Najpierw zastosujemy algorytm Euklidesa, aby obliczyć $N W D (225, 420)$ :

$420 = 1 \cdot 225 + 195$

$225 = 1 \cdot 195 + 30$

$195 = 6 \cdot 30 + 15$

$30 = 2 \cdot 15 + 0$

Zatem $N W D (225, 420) = 15$ .

Stąd $N W W (225, 420) = \frac{225 \cdot 420}{15} = 6300$ .

Przykład 6

Udowodnimy, że wzór $N W D (a, b, c) \cdot N W W (a, b, c) = a \cdot b \cdot c$ nie jest prawdziwy dla dowolnych liczb naturalnych $a$ , $b$ , $c$ .

Rozważmy liczby $6$ , $8$ i $10$ .

Wówczas łatwo sprawdzić, że $N W D (6, 8, 10) = N W D (3 \cdot 2, 2^{3}, 2 \cdot 5) = 2$ oraz $N W W (6, 8, 10) = N W W (3 \cdot 2, 2^{3}, 2 \cdot 5) = 3 \cdot 2 \cdot 2^{2} \cdot 5 = 120$ .

Wówczas $N W D (6, 8, 10) \cdot N W W (6, 8, 10) = 2 \cdot 120 = 240$ , zaś $6 \cdot 8 \cdot 10 = 480$ ,

zatem $N W D (6, 8, 10) \cdot N W W (6, 8, 10) \neq 6 \cdot 8 \cdot 10$ .

Jeśli chcemy obliczyć najmniejszą wspólną wielokrotnośćnajmniejsza wspólna wielokrotnośćnajmniejszą wspólną wielokrotność trzech liczb naturalnych, możemy najpierw wyznaczyć najmniejszą wspólną wielokrotność $w$ dwóch spośród trzech podanych liczb, a następnie najmniejszą wspólną wielokrotność liczby $w$ i trzeciej z rozważanych liczb. Innymi słowy zachodzi zależność:

N W W (a, b, c) = N W W (a, N W W (b, c))

Słownik

najmniejsza wspólna wielokrotność

najmniejszą wspólną wielokrotnością dodatnich liczb naturalnych $a$ i $b$ nazywamy najmniejszą dodatnią liczbę naturalną, która jest podzielna przez $a$ i przez $b$

największy wspólny dzielnik

największym wspólnym dzielnikiem liczb naturalnych $a$ i $b$ nazywamy największą liczbę naturalną dodatnią, która dzieli liczbę $a$ i liczbę $b$

Wprowadzenie

Gra edukacyjna

Słownik