Przeczytaj

Jeżeli znasz już wszystkie własności ciągu geometrycznego, wiesz kiedy szereg geometryczny jest zbieżny, zastosujemy tę wiedzę do rozwiązywania zadań o charakterze egzaminacyjnym. Na tej lekcji zebrana została kolekcja zadań, które są zadaniami typu maturalnego.

Przykład 1

Dany jest ciąg geometryczny $(a_{n})$ określony wzorem $a_{n} = {(\frac{1}{2 x - 371})}^{n}$ dla $n \geq 1$ . Wszystkie wyrazy tego ciągu są dodatnie. Wyznaczymy najmniejszą liczbę całkowitą $x$ , dla której nieskończony szereg $a_{1} + a_{2} + a_{3} + \dots$ jest zbieżny. Podamy dla wyznaczonej liczby sumę szeregu $a_{1} + a_{2} + a_{3} + \dots$ .

Rozwiązanie

Zapiszmy założenie:

$2 x - 371 \neq 0$

$x \neq 185, 5$ .

Ciąg $(a_{n})$ jest ciągiem geometrycznym o ilorazie $q = \frac{1}{2 x - 371}$ .

Wyrazy ciągu $(a_{n})$ są dodatnie, zatem $a_{1} > 0$ i $q > 0$ .

Ponieważ $a_{1} = q = \frac{1}{2 x - 371} > 0$ , więc $x \in (185, 5; \infty)$

Szereg geometryczny jest zbieżnyszereg geometryczny zbieżnySzereg geometryczny jest zbieżny wtedy i tylko wtedy, gdy $| q | < 1$ lub $a_{1} = 0$ .

Ponieważ $\frac{1}{2 x - 371} > 0$ , zatem musi być spełniony warunek $\frac{1}{2 x - 371} < 1$ , co jest równoważne warunkowi $1 < 2 x - 371$ , skąd dostajemy $x > 186$ .

Zatem szereg $\sum_{n = 1}^{\infty} a_{n}$ o wyrazach dodatnich jest zbieżny dla $x \in (186, \infty)$ .

Najmniejsza liczba całkowita należąca do przedziału $(186, \infty)$ to $187$ .

Dla $x = 187$ szereg ma postać $\sum_{n = 1}^{\infty} {(\frac{1}{2 \cdot 187 - 371})}^{n} = \sum_{n = 1}^{\infty} {(\frac{1}{3})}^{n}$ , zatem jego sumą jest $\frac{\frac{1}{3}}{1 - \frac{1}{3}} = \frac{1}{2}$ .

Przykład 2

Dany jest nieskończony ciąg okręgów $(o_{n})$ o równaniach $x^{2} + y^{2} = 2^{11 - n}$ , gdzie $n \geq 1$ . Niech $P_{k}$ będzie pierścieniem ograniczonym zewnętrznym okręgiem $o_{2 k - 1}$ i wewnętrznym okręgiem $o_{2 k}$ . Obliczymy sumę pól wszystkich pierścieni $P_{k}$ , gdzie $k \geq 1$ .

Rozwiązanie

Okrąg $o_{n}$ o równaniu $x^{2} + y^{2} = 2^{11 - n}$ jest okręgiem o środku $(0, 0)$ i promieniu $r_{n} = \sqrt{2^{11 - n}}$ .

Pole koła ograniczonego okręgiem $o_{n}$ jest równe $π r_{n}^{2} = π \cdot 2^{11 - n}$ .

Pierścień $P_{k}$ jest ograniczony z zewnątrz okręgiem $o_{2 k - 1}$ o polu $π r_{2 k - 1}^{2} = π \cdot 2^{11 - (2 k - 1)} = π \cdot 2^{12 - 2 k}$ i od wewnątrz okręgiem $o_{2 k}$ o polu $π r_{2 k}^{2} = π \cdot 2^{11 - 2 k}$ .

RCIaILLc6ZIYO

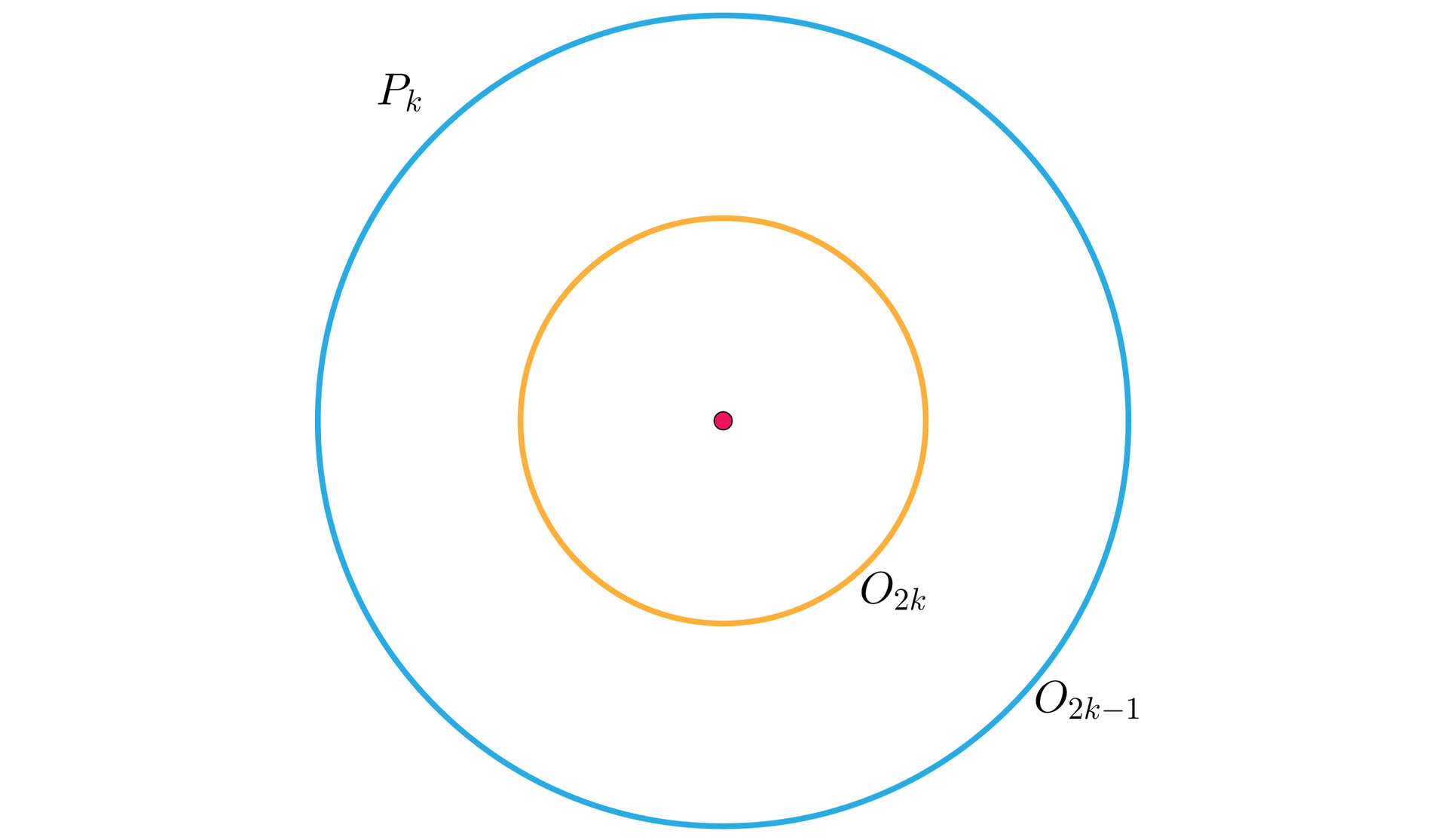
Na ilustracji przedstawiono pierścień Pk zbudowany w oparciu o dwa okręgi o wspólnym środku. Okrąg mniejszy opisany jest jako O2k, okrąf większy opisany jest jako O2k-1.

Pole pierścienia $P_{k}$ jest równe $P_{k} = π \cdot 2^{12 - 2 k} - π \cdot 2^{11 - 2 k} = π \cdot 2^{11 - 2 k} (2 - 1) = π \cdot 2^{11 - 2 k}$ .

Ponieważ mamy obliczyć sumę pól wszystkich pierścieni $P_{k}$ zauważmy, że ciąg pól $P_{k}$ jest ciągiem geometrycznym o ilorazie

$q = \frac{P_{k}}{P_{k - 1}} = \frac{π \cdot 2^{11 - 2 k}}{π \cdot 2^{11 - 2 (k - 1)}} = \frac{2^{11 - 2 k}}{2^{13 - 2 k}} = 2^{11 - 2 k - (13 - 2 k)} = 2^{- 2} = \frac{1}{4}$ .

Ponieważ iloraz spełnia warunek $|q| < 1$ , zatem szereg geometryczny $\sum_{n = 1}^{\infty} P_{n}$ jest zbieżny i jego suma jest równa: $S = \frac{2^{9} π}{1 - \frac{1}{4}} = \frac{2^{9} π}{\frac{3}{4}} = \frac{4 \cdot 2^{9} π}{3} = \frac{2^{11} π}{3} = \frac{2048 π}{3}$ .

Odpowiedź: Suma pól wszystkich pierścieni $P_{k}$ jest równa $\frac{2048 π}{3}$ .

Przykład 3

Wszystkie wyrazy nieskończonego ciągu geometrycznego $(a_{n})$ są liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest $100$ razy większa od sumy wszystkich wyrazów o numerach parzystych oraz $\log a_{1} + \log a_{2} + \log a_{3} + \dots + \log a_{100} = 100$ . Oblicz $a_{1}$ .

Rozwiązanie

Jeżeli iloraz ciągu $(a_{n})$ jest równy $q$ , to iloraz ciągu wyrazów o numerach nieparzystych jest równy $q^{2}$ oraz iloraz ciągu wyrazów o numerach parzystych jest równy $q^{2}$ . Ponieważ suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych, więc $q^{2} < 1$ . Ponieważ wszystkie wyrazy ciągu $(a_{n})$ są dodatnie, zatem $0 < q < 1$ .

Zapiszmy warunek w następujący sposób: suma wszystkich wyrazów o numerach nieparzystych jest dziesięć razy większa od sumy wszystkich wyrazów o numerach parzystych w następujący sposób:

$\frac{a_{1}}{1 - q^{2}} = 100 \frac{a_{1} q}{1 - q^{2}}$

Stąd otrzymujemy, że $q = \frac{1}{100}$ .

Teraz zajmiemy się drugim warunkiem:

$\log a_{1} + \log a_{2} + \log a_{3} + \dots + \log a_{100} = 100$ .

Wykorzystując wzór na sumę logarytmówsuma logarytmówsumę logarytmów przekształcamy równanie do postaci:

$\log (a_{1} \cdot a_{2} \cdot a_{3} \cdot \dots a_{100}) = 100$ .

Wykorzystujemy wzór na wyraz ogólny ciągu geometrycznego:

$\log (a_{1} \cdot a_{1} q \cdot a_{1} q^{2} \cdot \dots \cdot a_{1} q^{99}) = 100$

$\log (a_{1}^{100} \cdot {(\frac{1}{100})}^{1 + 2 + \dots + 99}) = 100$

Korzystamy z definicji logarytmu dziesiętnego:

$a_{1}^{100} \cdot {(\frac{1}{100})}^{1 + 2 + \dots + 99} = 10^{100}$

$a_{1}^{100} \cdot {(\frac{1}{100})}^{\frac{99 \cdot 100}{2}} = 10^{100}$

$a_{1} \cdot 10^{- 99} = 10$

Stąd otrzymujemy odpowiedź: $a_{1} = 10^{100}$ .

Przykład 4

Wartości funkcji $f : D \to ℝ$ spełniają dla każdego $x \in D$ następujące równanie

$1 + f (x) + {(f (x))}^{2} + (f (x))^{3} + \dots = \frac{1}{2 x^{2} - 3 x}$ , gdzie lewa strona równania jest sumą szeregu geometrycznego. Wyznaczymy dziedzinę, zbiór wartości i wzór funkcji $f$ .

Rozwiązanie

Aby szereg z lewej strony równania był zbieżny musi być spełniony warunek $|f (x)| < 1$ .

Wyznaczmy wzór funkcji $f$ zakładając, że jest spełniony warunek $|f (x)| < 1$ . Ze wzoru na sumę szeregu geometrycznego, mamy

$\frac{1}{1 - f (x)} = \frac{1}{2 x^{2} - 3 x}$

Stąd otrzymujemy:

$2 x^{2} - 3 x = 1 - f (x)$ .

Zatem wzór funkcji ma postać:

$f (x) = - 2 x^{2} + 3 x + 1$ .

Podamy dziedzinę korzystając z warunku $|f (x)| < 1$ :

$- 1 < - 2 x^{2} + 3 x + 1$ i $- 2 x^{2} + 3 x + 1 < 1$

Dostajemy zatem układ nierówności:

$2 x^{2} - 3 x - 2 < 0$ i $0 < 2 x^{2} - 3 x$ .

Rozwiązujemy nierówność $2 x^{2} - 3 x - 2 < 0$ :

$Δ = 9 + 16 = 25$

$x_{1} = - \frac{1}{2}$ , $x_{2} = 2$

Zatem $x \in (- \frac{1}{2}, 2)$ .

Rozwiązujemy nierówność $0 < 2 x^{2} - 3 x$ :

$0 < 2 x (x - \frac{3}{2})$

$x \in (- \infty, 0) \cup (\frac{3}{2}, + \infty)$

Zatem dziedziną funkcji jest część wspólna zbiorów: $(- \frac{1}{2}, 2)$ oraz $(- \infty, 0) \cup (\frac{3}{2}, + \infty)$ .

Zatem dziedziną funkcji jest zbiór: $(- \frac{1}{2}, 0) \cup (\frac{3}{2}, 2)$ .

Aby odczytać zbiór wartości funkcji $f$ , narysujemy wykres.

RYfSBpOCQcPNx

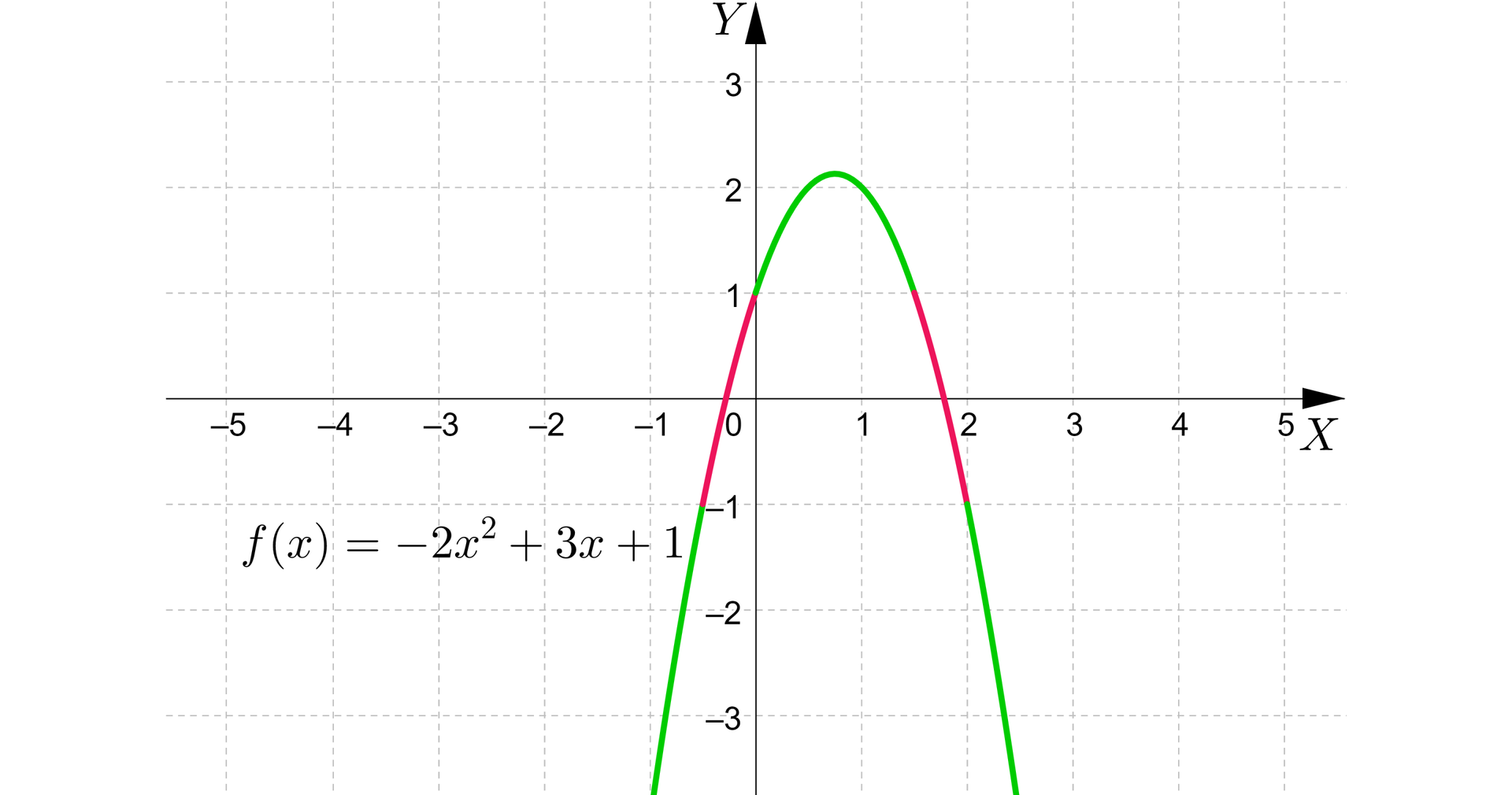
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie narysowano parabolę o ramionach skierowanych do dołu zadaną wzorem: fx=-2x2+3x+1. Wierzchołek paraboli znajduje się w pierwszej ćwiartce, a jej lewe ramię przecina oś Y w punkcie y równa się jeden. Funkcja ma dwa miejsca zerowe. Ramiona paraboli wyróżniono częściowo kolorem w dziedzinie, czyli w zbiorze -12,0∪32,2. Zbiór wartości w tym przedziale to zbiór -1, 1.

Zatem z wykresu odczytujemy, że zbiorem wartości jest przedział $(- 1, 1)$ .

Słownik

szereg geometryczny zbieżny

jeżeli $|q| < 1$ lub $a_{1} = 0$ , to szereg geometryczny $\sum_{n = 1}^{\infty} a_{1} \cdot q^{n - 1}$ jest zbieżny

jeżeli $a_{1} = 0$ , to $\sum_{n = 1}^{\infty} a_{1} \cdot q^{n - 1} = 0$

jeżeli $|q| < 1$ , to $\sum_{n = 1}^{\infty} a_{1} \cdot q^{n - 1} = \lim_{n \to \infty} S_{n} = \frac{a_{1}}{1 - q}$

suma logarytmów

jeżeli $x, y > 0$ oraz $a \in (0, 1) \cup (1, + \infty)$ , to $\log_{a} x + \log_{a} y = \log_{a} (x \cdot y)$

Wprowadzenie

Animacja

Słownik