Rozważmy ciąg, który składa się ze wszystkich liczb naturalnych: $\mathrm{1,2},\mathrm{3,4},...$. Ciąg taki możemy zapisać wzorem

Jeżeli usuniemy z tego ciągu kilka jego początkowych wyrazów, np. $a_1,a_2,a_3$, to otrzymamy ciąg $\mathrm{4,5,6,7},...$. Ten nowo otrzymany ciąg składa się z prawie wszystkich wyrazów ciągu $\left(a_n\right)$, gdyż nie zawiera jedynie trzech jego wyrazów $a_1,a_2,a_3$. Podobnie jeśli wzięlibyśmy pod uwagę ciąg

Powyższy ciąg zawiera wszystkie wyrazy ciągu $\left(a_n\right)$ za wyjątkiem wyrazów $\mathrm{101,102},103,\dots ,999$. Wyrazów tych jest dokładnie $899$ a zatem ilość skończona. Stąd możemy powiedzieć, że rozważany ciąg zawiera prawie wszytskie wyrazy ciągu $\left(a_n\right)$, tzn. wszytskie poza skończoną ilością (która w tym przypadku jest równa $899$).

Rozważmy następujący ciąg

Ciąg ten możemy zapisać wzorem $a_n=2n.$ Jest to ciąg, który składa się ze wszytskich liczb naturalnych parzystych. Każdy wyraz tego ciągu jest też oczywiście wyrazem ciągu $a_n=n$, który z kolei składa się ze wszystkich liczb naturalnych. Jednak ciąg $\mathrm{2,4},\mathrm{6,8},\dots$ nie zawiera żadnej liczby nieparzystej, które też są wyrazamu ciągu $a_n=n$. Stąd wynika, że ciąg $a_n=2n$ pomimo tego, że zawiera nieskończenie wiele wyrazów ciągu $a_n=n$ (tzn. wszystkie liczby naturalne parzyste) nie zawiera prawie wszystkich jego wyrazów, gdyż nie zawiera liczb nieparzystych, których jest nieskończenie wiele.

Niech dany będzie ciąg $(a_n)$ oraz pewien zbiór $A\subset\mathbb{R}$. Powiemy, że do zbioru $A$ należą prawie wszystkie wyrazy ciągu $(a_n)$, jeśli istnieje co najwyżej skończona liczba wyrazów ciągu $(a_n)$, które nie należą do zbioru $A$.

Rozważmy ciąg

Wypiszmy kilka kolejnych wyrazów tego ciągu

Sprawdzimy do których z podanych niżej zbiorów należą prawie wszystkie wyrazy danego ciągu.

Na początek zauważmy, że dany ciąg jest ciągiem malejącym, gdyż dla dowolnej liczby $n\in\mathbb{N}$, mamy

Wynika stąd, że największym wyrazem tego ciągu jest wyraz $a_1=2$. Wnioskujemy stąd, że $a_n\le 2$ dla każdego $n\in\mathbb{N}$. Z drugiej strony

dla każdego $n\in\mathbb{N}$. Reasumując możemy powiedzieć, że wszystkie wyrazy ciągu $(a_n)$ należą do przedziału $(1,2\rangle$.

• $A=(0,1)$. 
  Ponieważ przedział $A$ jest rozłączny z przedziałem $(1,2\rangle$ więc nie należy do niego żaden wyraz ciągu $(a_n)$. W szczególności zatem nie należą do niego prawie wszystkie wyrazy ciągu $(a_n)$.

• $B=(1,2)$. 
  Zauważmy, że do przedziału $B$ nie należy tylko pierwszy wyraz naszego ciągu, który jest równy $2$. Zatem do przedziału $B$ należą prawie wszystkie wyrazy tego ciągu (wszystkie poza pierwszym).

• $C=\langle\frac{3}{4},\frac{5}{4}\rangle$. 
  Do przedziału $C$ nie należą wyrazy $a_1=2,a_2=1\frac{1}{2},\ a_3=1\frac{1}{3}$. Wyraz $a_4=1\frac{1}{4}$ należy już do przedziału $C$. Ponieważ nasz ciąg jest malejący oraz wszystkie jego wyrazy są większe od $1$ więc wyrazy $a_5,a_6,a_7,\ldots$ również należą do przedziału $C$. Oznacza to, że prawie wszystkie wyrazy ciągu $(a_n)$ należą do przedziału $C$ (w tym przypadku wszystkie poza pierwszymi trzema).

• $D=\langle\frac{6}{5}, 2\rangle$. 
  Do przedziału $D$ należą wyrazy $a_1=2, a_2=1\frac{1}{2}, a_3=1\frac{1}{3}, a_4=1\frac{1}{4}, a_5=1\frac{1}{5}$. Ponieważ $a_6=1+\frac{1}{6}=\frac{7}{6}\notin D$ oraz ciąg $(a_n)$ jest malejący więc kolejne wyrazy $(a_7,a_8,\ldots)$ również nie należą do przedziału $D$. Zatem prawie wszystkie wyrazy ciągu $(a_n)$ nie należą do przedziału $D$ (gdyż należy do niego tylko pięć pierwszych wyrazów).

Rozważmy ciąg

Weźmy dowolne otoczenie liczbyotoczenie punktuotoczenie liczby $0$, tzn. zbiór wszystkich liczb rzeczywistych spełniających nierówność $|x-0|\lt \varepsilon$, gdzie $\epsilon$ jest dowolną, ustaloną dodatnią liczbą rzeczywistą. Zbiór ten można zapisać w postaci przedziału $(-\epsilon ,\epsilon )$. Zauważmy, że wybierając dostatecznie dużą liczbę naturalną $N\in \mathbb{N}$ ułamek $\frac{1}{N}$ będzie mniejszy od wybranej dodatniej liczby $\epsilon$. Ponieważ $\frac{1}{N+1}<\frac{1}{N}$ dla dowolnej liczby naturalnej $N$ więc wszystkie wyrazy ciągu $a_n=\frac{1}{n}$ począwszy od wyrazu $a_N$ należą do przedziału $(-\epsilon ,\epsilon )$. Obserwacja ta prowadzi do wniosku, że dla dowolnej liczby dodatniej $\epsilon$ do przedziału $(-\epsilon ,\epsilon )$ należą prawie wszystkie wyrazy ciągu $a_n=\frac{1}{n}$ (tzn. wszytskie za wyjątkiem wyrazów $a_1,a_2,a_3,\dots ,a_{N-1}$). Ilustruje to poniższa grafika.

R16aC1gv3LT0u

Ilustracja przedstawia poziomą oś $X$ od zera do jeden. Na osi zaznaczono zamalowanymi punktami następujące liczby: $0, \frac{1}{N}, \frac{1}{N-1}, \frac{1}{2}, 1$. Pomiędzy liczbami $\frac{1}{N}$ i $\frac{1}{N-1}$ oznaczono na osi również epsilon. Nad osią poziomą klamrą objęto fragment osi od zera do epsilon i podpisano następująco: "prawie wszystkie wyrazy ciągu $a_n=\frac{1}{n}$.

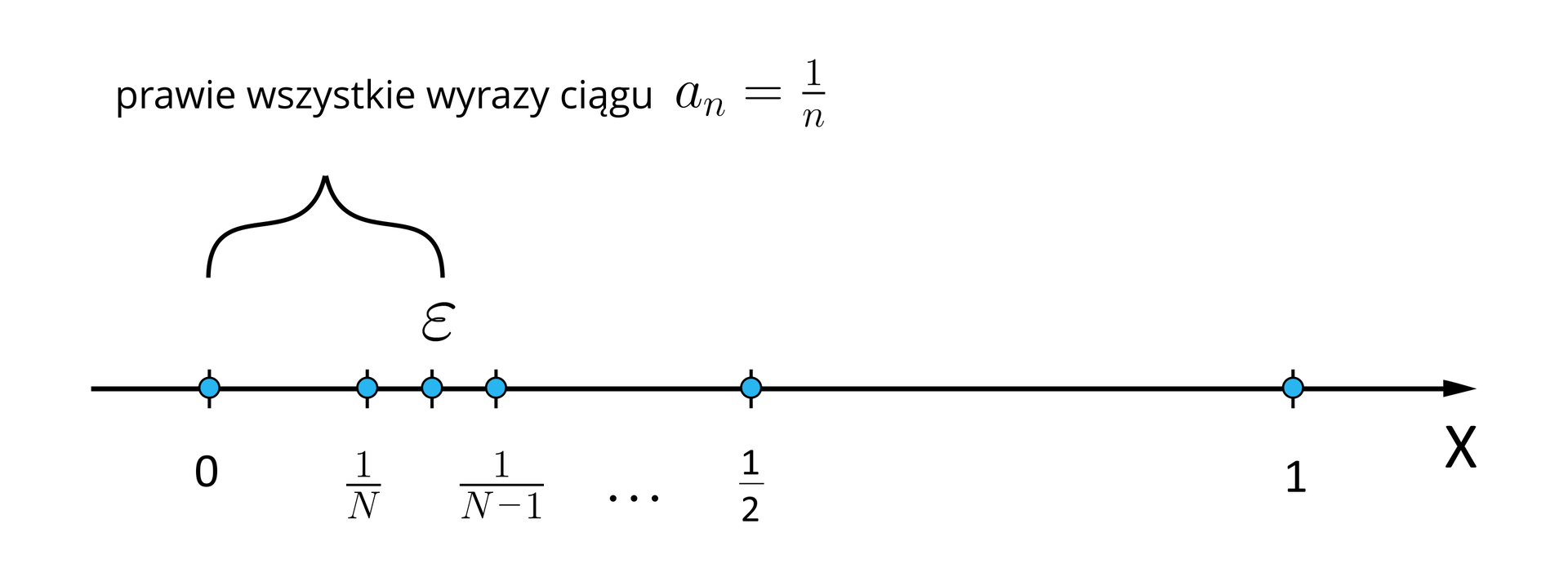
Oczywiście im liczba $\varepsilon$ będzie bliżej zera, tym liczba naturalna $N$ będzie musiała być większa aby warunek $\frac{1}{N}\lt \varepsilon$ był spełniony. Jednak wciąż nierówność ta będzie spełniona dla prawie wszystkich wyrazów ciągu $a_n=\frac{1}{n}$ ( tzn. dla ułamków $\frac{1}{N}, \frac{1}{N+1}, \frac{1}{N+2}, \ldots$).

otoczeniem punktu $x_0$ o promieniu $\epsilon >0$ nazywamy zbiór