Obliczymy wysokość budynku, którego cień ma długość $18 \mathrm{m}$ wiedząc, że kąt padania promieni słonecznych wynosi $40°$. Wynik podamy z dokładnością do $\mathrm{0,1} \mathrm{m}$.

R1XFXvI3bfT7x

Rysunek ilustruje zadanie. Głównym elementem rysunku jest trójkąt prostokątny $ABC$, który stopniowo opiszemy. W lewej górnej części ilustracji narysowano Słońce, od którego poprowadzono ukośny odcinek nachylony pod kątem czterdziestu stopni do poziomu. Na tym odcinku zaznaczono dwa punkty. Mniej więcej w jednej trzeciej długości oznaczono punkt $C$, a na końcu punkt $B$. Poniżej, trochę na prawo od Słońca narysowano także prostokąt, którego podstawa jest wyraźnie krótsza od boków. Prawy górny wierzchołek prostokąta pokrywa się z punktem $C$ odcinka poprowadzonego ze Słońca. Pionowo pod punktem $C$ zaznaczono punkt $A$ na prawym dolnym wierzchołku prostokąta. Odcinek $CA$ oznaczono jako $h$ i przy wierzchołku $A$ zaznaczono kąt prosty wewnątrz trójkąta. Podstawa trójkąta prostokątnego to poziomy odcinek $AB$ o długości 18 metrów. Przy wierzchołku zaznaczono kąt wewnętrzny o mierze czterdziestu stopni.

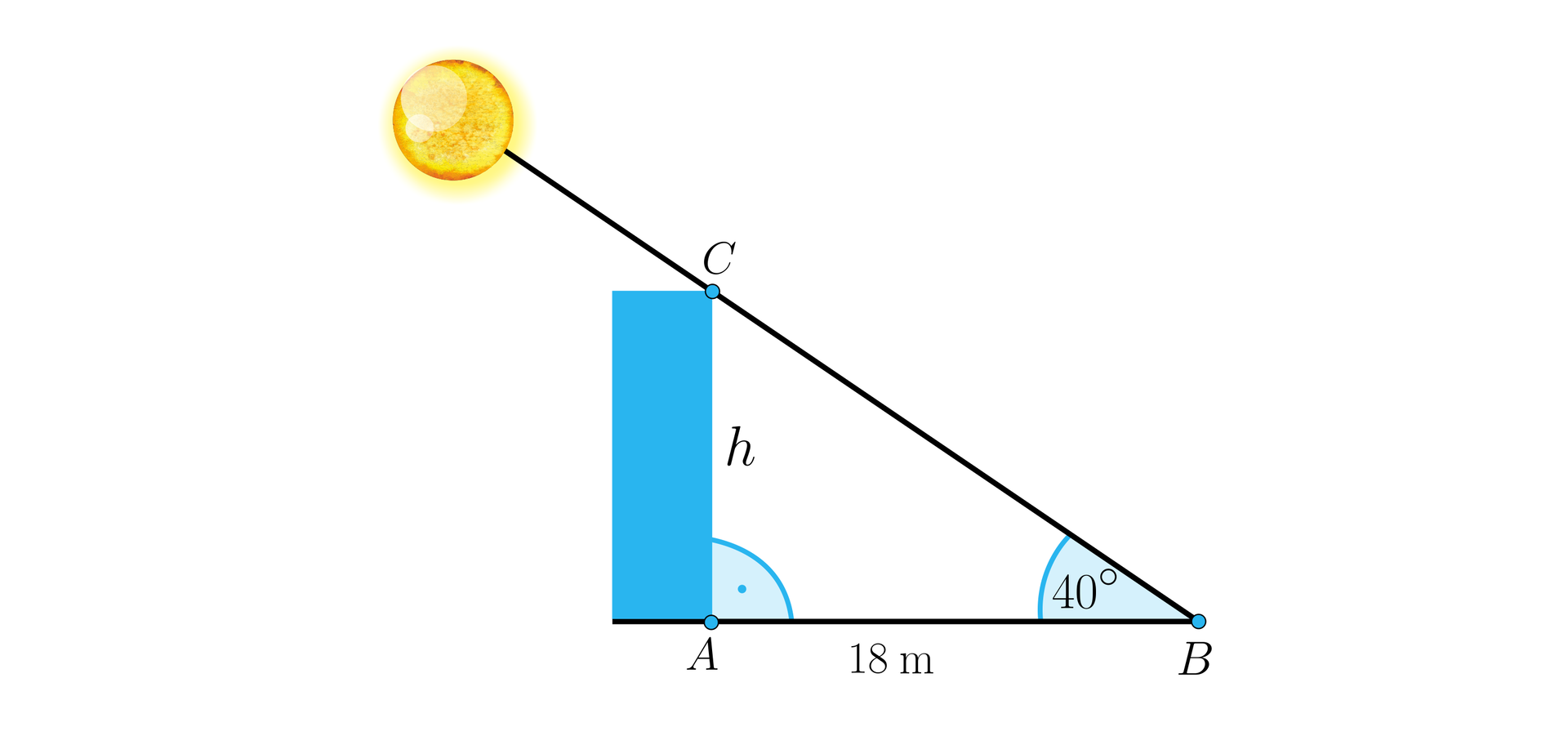
Trójkąt $ABC$ jest prostokątny, więc z definicji tangensatangens kąta ostrego $\alpha$ w trójkącie prostokątnymtangensa mamy:

$\mathrm{tg}40°=\frac{h}{18}$,

z tablic odczytujemy $\mathrm{tg}40°\approx \mathrm{0,8391}$.

Po przekształceniach otrzymujemy:

$18·0,8391\approx h$, czyli

$h\approx \mathrm{15,1038}\approx \mathrm{15,1} \mathrm{m}$.

Odpowiedź: Budynek ma około $\mathrm{15,1} \mathrm{m}$ wysokości.

Krzywa wieża w Ząbkowicach Śląskich ma wysokość $34 \mathrm{m}$ i jej odchylenie od pionu wynosi $\mathrm{2,14} \mathrm{m}$. Wyznaczmy kąt, jaki tworzy z powierzchnią ziemi ściana wieży. O ile stopni odchylona jest wieża od pionu? Podamy wynik z dokładnością do $0,1°$.

Rf5PRA7c2ddUV

Rysunek przestawia równoległobok o poziomych podstawach i ukośnych bokach. Figura położona jest na poziomej prostej. Z prawego górnego wierzchołka upuszczono pionowy odcinek narysowany linią przerywaną. Odcinek ten opisany jest jako $34$ metry i jest jednym z boków trójkąta prostokątego. Między prawym ukośnym bokiem równoległoboku a pionowym odcinkiem zaznaczono kąt beta. Bok ten jest drugim bokiem trójkąta prostokątnego. Kąt między pionowym odcinkiem narysowanym linią przerywaną a poziomą prostą oznaczono jako kąt prosty. Kąt między poziomą prostą a prawym bokiem równoległoboku wynosi alfa. Kąty alfa i beta są kątami wewnętrznymi trójkąta. Podstawa trójkąta prostokątnego wynosi $2,14$ metra.

Powstały trójkąt jest prostokątny.

$\alpha$ – kąt, jaki tworzy ściana wieży z powierzchnią ziemi.

Z definicji tangensatangens kąta ostrego $\alpha$ w trójkącie prostokątnymtangensa mamy:

$\mathrm{tg}\alpha =\frac{34}{2,14}\approx 15,8879$.

Za pomocą kalkulatora znajdujemy przybliżoną wartość kąta $\alpha$:

$\alpha \approx 86,398498$, a zatem

$\alpha \approx 86,4°$.

$\beta$ - kąt odchylenia wieży od pionu.

$\beta =90°-\alpha$, a zatem

$\beta \approx 90°-86,4°\approx 3,6°$.

Odpowiedź: Z powierzchnią ziemi ściana wieży tworzy kąt około $86,4°$. Wieża jest odchylona od pionu o około $3,6°$.

Jedną z trzech największych piramid egipskich w Gizie jest piramida Chefrena. Długość boku u podstawy tej piramidy wynosi $214,5 \mathrm{m}$, a ściany boczne są nachylone do podstawy pod kątem $53°7\text{'}48\text{'}\text{'}\approx 53°$ (kąt zaznaczono na rysunku). Obliczymy wysokość tej piramidy. Wynik podamy z dokładnością do $1 \mathrm{m}$.

Piramida ma kształt ostrosłupa o podstawie kwadratu. Na rysunku przedstawiamy sytuację z zadania:

RdO3LSnrNy6i3

Rysunek przedstawia ostrosłup prawidłowy czworokątny o krawędzi podstawy $a$, wysokości $h$ i kącie nachylenia ściany bocznej do podstawy o mierze alfa. Na rysunku przedstawiono też wyróżniony kolorem trójkąt prostokątny o przyprostokątnych $h$ i $b$, gdzie $b$ jest długości połowy krawędzi podstawy $a$. Przeciwprostokątna tego trójkąta poprowadzona jest przez środek ściany do wierzchołka bryły. W trójkącie zaznaczono kąt alfa, czyli kąt nachylenia ściany bocznej do podstawy.

gdzie

$h$ – wysokość piramidy,
$\alpha$ – kąt nachylenia ściany bocznej do podstawy piramidy,
$\alpha \approx 53°$.

Rozważany trójkąt jest prostokątny – długości jego przyprostokątnych to: $h$ i $b$. Z rysunku wynika, że $b=\frac{a}{2}$.

Z definicji tangensa mamy:

$\mathrm{tg}\alpha =\frac{h}{b}=\frac{h}{{\displaystyle \frac{1}{2}}a}=\frac{2h}{a}$.

Podstawiamy dane z zadania:

$\mathrm{tg}53°=\frac{2h}{214,5}$,

$2·h=\mathrm{tg}53°·214,5\approx 1,3270·214,5\approx 284,6415\approx 284,6$,

$h\approx \frac{284,6}{2}\approx 142,3\approx 142 \mathrm{m}$.

Odpowiedź: Wysokość piramidy Chefrena wynosi około $142 \mathrm{m}$.

Kolej gondolowa na Stok Izerski ma długość trasy $2171 \mathrm{m}$. Stacja dolna tej kolei znajduje się na wysokości $617 \mathrm{m}$ $\text{n. p. m.}$, a górna na wysokości $1060 \mathrm{m}$ $\text{n. p. m.}$ Obliczymy średnie nachylenie stoku. Podamy wynik z dokładnością do $0,1°$.
Zakładając, że wjazd gondoli odbywa się po linii prostej, obliczymy, jaka jest odległość stacji dolnej od punktu, który leży na tej samej wysokości, ale pod stacją górną.

RPJR40VCqygdM

Rysunek przedstawia trójkąt prostokątny $ABC$, gdzie bok $AB$ jest poziomą podstawą trójkąta oznaczoną jako $x$. Przy wierzchołku $A$ zaznaczono kąt alfa, przy wierzchołku $B$ znajduje się kąt prosty. Przez podstawę poprowadzono linię przerywaną i opisano przy wierzchołku $A$ następująco: stacja dolna kolei, 617 m n. p. m. Bok trójkąta $CB$ jest pionową przyprostokątną i opisany jest jako $h$. Na ilustracji poprowadzono drugą poziomą przerywaną linię przechodzącą przez wierzchołek $C$. Linia ta symbolizuje poziom 1060 m n. p. m. Przy wierzchołki $C$ dodano następujący opis: stacja górna kolei. Przekątna trójkąta opisana jest następująco: 2171 m.

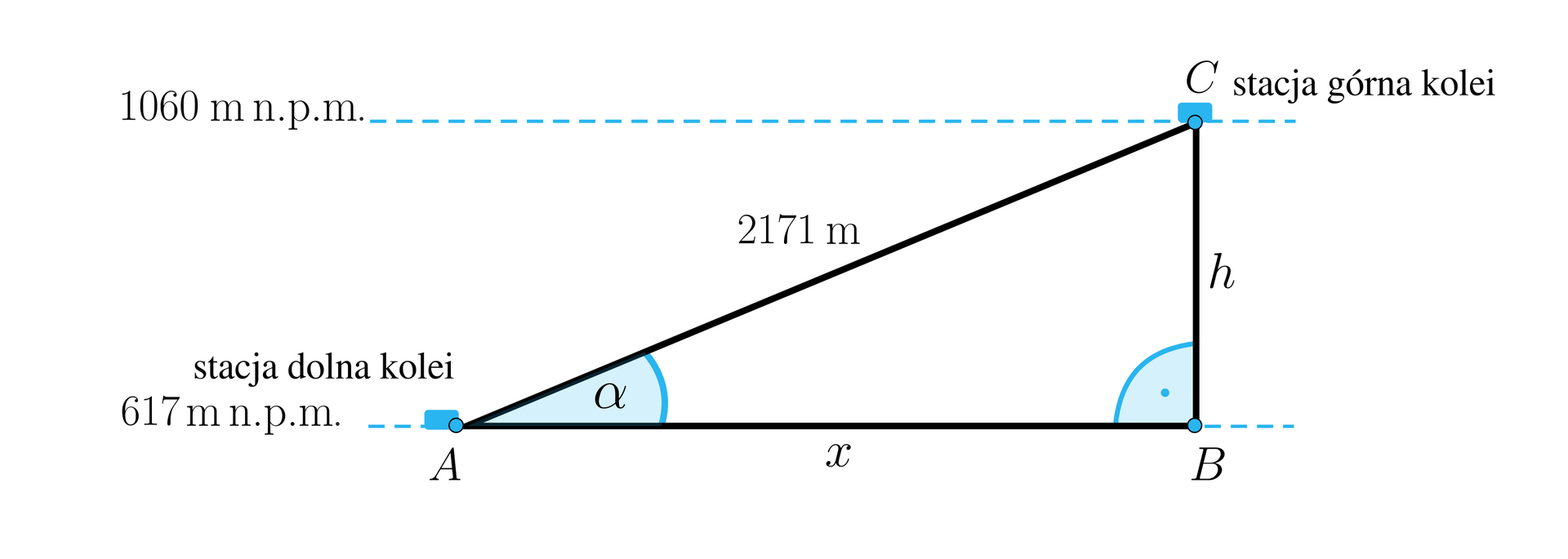
Różnica wysokości między stacją górną a dolną jest długością boku $BC$ trójkąta $ABC$. Oznaczmy:

$\left|BC\right|=h$

$h=1060-617=443 \mathrm{m}$.

Trójkąt $ABC$ jest prostokątny, więc z definicji sinusasinus kąta ostrego $\alpha$ w trójkącie prostokątnymsinusa mamy:

$\mathrm{sin\alpha }=\frac{h}{\left|AC\right|}$, gdzie

$h=443 \mathrm{m}$ oraz $\left|AC\right|=2171 \mathrm{m}$,

$\sin \alpha =\frac{443}{2171}\approx 0,2040$.

Za pomocą kalkulatora obliczamy  przybliżoną wartość kąta $\alpha$:

$\alpha =11,77°\approx 12°$.

Odległość stacji dolnej od punktu, który leży na tej samej wysokości, ale pod stacją górną, policzymy z definicji funkcji cosinuscosinus kąta ostrego $\alpha$ w trójkącie prostokątnymcosinus.

Podstawiając $\cos 12°\approx 0,9781$, otrzymujemy

$0,9781\approx \frac{x}{2171}$.

Zatem

$x\approx 0,9781·2171\approx 2123,4\approx 2123 \mathrm{m}$.

Odpowiedź: Średnie nachylenie stoku wynosi około $12°$, a punkt, który leży na tej samej wysokości, ale pod stacją górną jest odległy o około $2123 \mathrm{m}$ od stacji dolnej.

Wał ochronny ma przekrój trapezu równoramiennego, przy czym górna szerokość wału wynosi $4 \mathrm{m}$, natomiast boczne nasypy o długości $7 \mathrm{m}$ są nachylone do poziomu pod kątem $27°$. Oblicz dolną szerokość wału oraz jego wysokość.

R1Ir5UijA9Xzh

Rysunek przedstawia trapez równoramienny $ABCD$. Wewnątrz trapezu utworzono prostokąt, upuszczając z wierzchołków podstawy górnej dwa pionowe odcinki na podstawę dolną. Te odcinki to $DE$ oraz $CF$, przy czym odcinek $DE$ jest dodatkowo opisany jako wysokość trapezu, czyli $h$. Przy wierzchołkach $E$ i $F$ oznaczoną kąty proste, natomiast przy wierzchołkach podstawy dolnej $A$ oraz $B$ oznaczono kąty 27 stopni. Ramiona trapezu mają długość 7 metrów każde, a górna podstawa ma 4 metry.

$\left|EF\right|=\left|DC\right|=4 \mathrm{m}$

Trapez $ABCD$ jest równoramienny, więc $\left|AE\right|=\left|FB\right|$.

Szerokość dolnej części wału wynosi: $\left|AB\right|=\left|AE\right|+\left|EF\right|+\left|FB\right|$, a ponieważ $\left|AE\right|=\left|FB\right|$, to:

$\left|AB\right|=2\left|AE\right|+\left|DC\right|$

$\left|DC\right| =4 \mathrm{m}$, więc

$\left|AB\right|=2\left|AE\right|+4$.

Aby wyznaczyć dolną część wału, należy obliczyć długość odcinka $AE$.

Trójkąt $AED$ jest prostokątny, zatem z definicji funkcji cosinuscosinus kąta ostrego $\alpha$ w trójkącie prostokątnymcosinus mamy:

$\cos \alpha =\frac{\left|AE\right|}{\left|AD\right|}$.

Podstawiając: $\alpha =27°$, $\left|AD\right|=7$, otrzymujemy

$\cos 27°=\frac{\left|AE\right|}{7}$.

Z tablic odczytujemy wartość $\cos 27°\approx 0,8910$,

$0,8910\approx \frac{\left|AE\right|}{7}$.

Stąd

$\left|AE\right|\approx 7·0,8910\approx 6,237\approx 6,2$.

Wynik podamy z przybliżeniem do $0,1 \mathrm{m}$: $\left|AE\right|\approx 6,2 \mathrm{m}$.

Szerokość dolnej części wału, czyli długość podstawy trapezu, wynosi:

$\left|AB\right|\approx 2\left|AE\right|+4\approx 12,4+4\approx 16,4 \mathrm{m}$.

Wysokość wału obliczymy z definicji funkcji sinussinus kąta ostrego $\alpha$ w trójkącie prostokątnymsinus.

$\sin 27°=\frac{\left|ED\right|}{\left|AD\right|}$

$\left|ED\right|=h, \left|AD\right|=7 \mathrm{m}$

$\sin 27°=\frac{h}{7}$

$h·7=\sin 27°$

Ponieważ $\sin 27°\approx 0,4550$ (odczytujemy z tablic trygonometrycznych), to

$h\approx 7·0,4540\approx 3,178\approx 3,2$.

Wynik podamy z przybliżeniem do $0,1 \mathrm{m}$:

$h\approx 3,2 \mathrm{m}$.

Odpowiedź: Dolna część wału ma szerokość około $16,4 \mathrm{m}$. Wysokość wału wynosi około $3,2 \mathrm{m}$.

nazywamy stosunek długości przyprostokątnej przeciwległej kątowi $\alpha$ do długości przeciwprostokątnej.

stosunek długości przyprostokątnej przyległej do kąta $\alpha$ do długości przeciwprostokątnej

stosunek długości przyprostokątnej przeciwległej kątowi $\alpha$ do długości przyprostokątnej przyległej do kąta $\alpha$