Przeczytaj

koło

Definicja: koło

Kołem o środku $O$ i promieniu $r$ nazywamy zbiór wszystkich punktów $P$ płaszczyzny, których odległość od punktu $O$ jest mniejsza lub równa $r$ .

Punkt $P$ należy do koła o środku w punkcie $O = (a, b)$ i promieniu $r$ wtedy i tylko wtedy, gdy spełniona jest nierówność $| O P | \leq r$ .

Powyższy warunek możemy zapisać następująco: $\sqrt{{(x - a)}^{2} + {(y - b)}^{2}} \leq r$ , co prowadzi do nierówności ${(x - a)}^{2} + (y - b)^{2} \leq r^{2}$ przedstawiającej koło o środku w punkcie $O = (a, b)$ i promieniu $r$ .

Przykład 1

Nierówność $x^{2} + {(y - 1)}^{2} \leq 4$ przedstawia koło o środku w punkcie $(0, 1)$ i promieniu $2$ .

RDDUjGmfEQAr1

Grafika przedstawia poziomą oś x od minus pięciu do pięciu oraz pionową oś y od minus dwóch do trzech. Na płaszczyźnie znajduje się koło, o środku O w punkcie początek nawiasu, 0, 1, zamknięcie nawiasu. Brzeg koła przechodzi przez punkt początek nawiasu, 0, 3, zamknięcie nawiasu.

Przykład 2

Znajdziemy środek i promień koła danego nierównością $x^{2} + y^{2} - 4 x - 4 y - 8 \leq 0$ .

Rozwiązanie:

Aby wyznaczyć promień i współrzędne środka koła sprowadzimy powyższą nierówność do postaci: ${(x - a)}^{2} + {(y - b)}^{2} \leq r^{2}$ .

W tym celu przekształcamy lewą stronę nierówności wykorzystując wzory skróconego mnożenia:

$x^{2} + y^{2} - 4 x - 4 y - 8 = (x^{2} - 2 \cdot 2 x + 4) - 4 + (y^{2} - 2 \cdot 2 y + 4) - 4 - 8 =$ $= {(x - 2)}^{2} + {(y - 2)}^{2} - 16 \leq 0$ .

Otrzymujemy nierówność opisującą koło w postaci: ${(x - 2)}^{2} + {(y - 2)}^{2} \leq 16$ .

Możemy teraz odczytać, że nierówność $x^{2} + y^{2} - 4 x - 4 y - 8 \leq 0$ przedstawia koło o środku $O = (2, 2)$ i promieniu $4$ .

Przykład 3

Sprawdzimy, czy nierówności:

a) $x^{2} + y^{2} - x - y \leq 0$

b) $x^{2} + y^{2} + 12 x - 2 y + 49 \leq 0$

opisują koło.

Rozwiązanie:

Musimy sprawdzić, czy te nierówności można sprowadzić do postaci $(x - a)^{2} + (y - b)^{2} \leq r^{2}$ zwanej postacią kanoniczną.

a) Sprawdźmy pierwszą nierówność: $x^{2} + y^{2} - x - y \leq 0$ .

Zacznijmy od rozważenia równoważnej postaci: $x^{2} - x + y^{2} - y \leq 0$ :

Będziemy przekształcać równoważnie nierówności by ostatecznie sprowadzić je do postaci kanonicznej. $x^{2} - 2 \cdot \frac{1}{2} x + y^{2} - 2 \cdot \frac{1}{2} y \leq 0$

$x^{2} - 2 \cdot \frac{1}{2} x + \frac{1}{4} - \frac{1}{4} + y^{2} - 2 \cdot \frac{1}{2} y + \frac{1}{4} - \frac{1}{4} \leq 0$

${(x - \frac{1}{2})}^{2} - \frac{1}{4} + {(y - \frac{1}{2})}^{2} - \frac{1}{4} \leq 0$

${(x - \frac{1}{2})}^{2} + {(y - \frac{1}{2})}^{2} \leq \frac{1}{2}$

${(x - \frac{1}{2})}^{2} + {(y - \frac{1}{2})}^{2} \leq {(\frac{\sqrt{2}}{2})}^{2}$ .

Tym samym nierówność $x^{2} + y^{2} - x - y \leq 0$ opisuje koło o środkukoło o środku O i promieniu rkoło o środku $(\frac{1}{2}, \frac{1}{2})$ i promieniukoło o środku O i promieniu ri promieniu $\frac{\sqrt{2}}{2}$ .

b) Sprawdźmy drugą nierówność:

$x^{2} + y^{2} + 12 x - 2 y + 49 \leq 0$ .

Podobnie jak poprzednio będziemy dążyć do postaci kanonicznej, w tym celu przekształcimy nierówności równoważnie: $x^{2} + 12 x + y^{2} - 2 y + 49 \leq 0$

${(x + 6)}^{2} - 36 + {(y - 1)}^{2} - 1 + 49 \leq 0$

${(x + 6)}^{2} + {(y - 1)}^{2} \leq - 12$

Liczba $- 12$ nie jest kwadratem żadnej liczby rzeczywistej, więc nierówność $x^{2} + y^{2} - 4 x - 4 y - 8 \leq 0$ nie przedstawia koła.

Wniosek:

Nierówność $x^{2} + y^{2} - 2 a x - 2 b y + c \leq 0$ przedstawia koło wtedy i tylko wtedy, gdy $a^{2} + b^{2} - c > 0$ , promieniem tego koła jest liczba $\sqrt{a^{2} + b^{2} - c}$ a środkiem punkt $(a, b)$ .

Dowód: Nierówność $x^{2} + y^{2} - 2 a x - 2 b y + c \leq 0$ możemy zapisać równoważnie jako $(x - a)^{2} - a^{2} + (y - b)^{2} - b^{2} + c \leq 0$ , czyli $(x - a)^{2} + (y - b)^{2} \leq a^{2} + b^{2} - c$ . Jest to postać kanoniczna równania okręgu o promieniu $r$ i środku w punkcie $(a, b)$ , gdy $r^{2} = a^{2} + b^{2} - c$ . Stąd warunek $a^{2} + b^{2} - c > 0$ .

Przykład 4

Zbadamy, czy punkt $P = (- 1, 0)$ leży wewnątrz koła $(x - 1)^{2} + (y + 3)^{2} \leq 5$ .

Rozwiązanie:

Sprawdzamy, czy współrzędne punktu $P$ spełniają nierówność koła: $(x - 1)^{2} + (y + 3)^{2} \leq 5$ .

Podstawiając współrzędne do lewej stony nierówności koła otrzymujemy: $(- 1 - 1)^{2} + (0 + 3)^{2} = 4 + 9 > 5$

Zatem punkt $P$ nie należy do koła danego nierównością $(x - 1)^{2} + (y + 3)^{2} \leq 5$ .

Przedstawmy tę sytuację w układzie współrzędnych:

Z postaci kanonicznej odczytujemy, że przedstawia ona koło o środku w punkcie $O = (1, - 3)$ i promieniu $r = \sqrt{5}$ .

RRLJlYcdQ7eMb

Grafika przedstawia poziomą oś x od minus pięciu do pięciu oraz pionową oś y od minus sześciu do jeden. Na płaszczyźnie znajduje się koło, o środku O w punkcie początek nawiasu, 1, minus 3, zamknięcie nawiasu. Okrąg wyznaczający koło przecina oś y w punktach początek nawiasu, 0, minus 1, zamknięcie nawiasu oraz początek nawiasu, 0, minus 5, zamknięcie nawiasu. Dodatkowo na płaszczyźnie znajduje się punkt P o współrzędnych początek nawiasu, minus 1, 0, zamknięcie nawiasu.

Przykład 5

Dany jest prostokąt $A B C D$ o wierzchołkach $A = (1, 1)$ , $B = (7, 1)$ , $C = (7, 5)$ i $D = (1, 5)$ . Wyznaczymy minimalny promień koła, o środku umieszczonym w środku boku $A B$ , aby w całości koło zakryło ten prostokąt. Napiszemy nierówność opisującą to koło.

Rozwiązanie:

Oznaczmy przez $O$ środek odcinka $A B$ . Niech zatem $O = (x_{o}, y_{o})$ , gdzie $x_{o} = \frac{x_{A} + x_{B}}{2}$ , $y_{o} = \frac{y_{A} + y_{B}}{2}$ .

Po podstawieniu współrzędnych otrzymujemy: $x_{0} = \frac{x_{A} + x_{B}}{2} = \frac{1 + 7}{2} = 4$ i $y_{0} = \frac{y_{A} + y_{B}}{2} = \frac{1 + 1}{2} = 1$ .

RpVsmD3uR9MdR

Grafika przedstawia poziomą oś x od minus dwóch do ośmiu oraz pionową oś y od minus jeden do pięciu. Na płaszczyźnie znajduje się prostokąt z wierzchołkami o współrzędnych : A początek nawiasu, 1, 1, zamknięcie nawiasu, B początek nawiasu, 7, 1, zamknięcie nawiasu, C początek nawiasu, 7, 5, zamknięcie nawiasu, D początek nawiasu, 1, 5, zamknięcie nawiasu. Na odcinku AB zaznaczony został punkt O, którego współrzędne to początek nawiasu, 4, 1, zamknięcie nawiasu. Punkt O jest połączony z punktem C.

Zauważmy, że minimalny promień koła powinien być równy długości odcinka $O C$ . Długość odcinka $O C$ obliczymy ze wzoru na odległość dwóch punktów $A = (x_{1}, y_{1})$ i $B = (x_{2}, y_{2})$ : $| A B | = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ .

W naszym przypadku, $r = | O C |$ , $C = (7, 5)$ i $O = (4, 1)$ .

$r = | O C | = \sqrt{{(7 - 4)}^{2} + {(5 - 1)}^{2}} = \sqrt{3^{2} + 4^{2}} = \sqrt{25} = 5$ .

Nierówność opisująca koło ma zatem postać: ${(x - 4)}^{2} + {(y - 1)}^{2} \leq 25$ .

RpQiunDoHZp8E

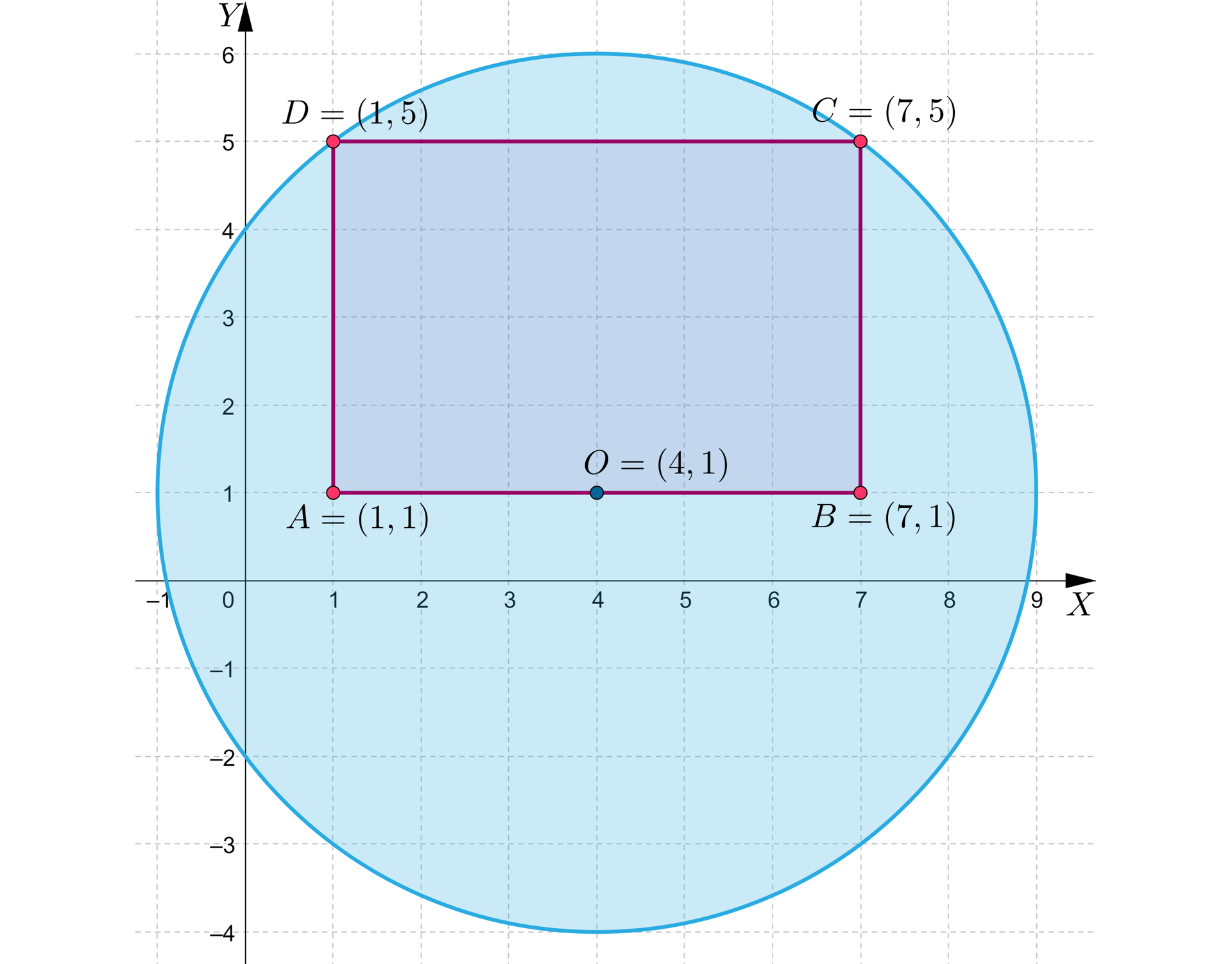
Grafika przedstawia poziomą oś x od minus jeden do dziewięciu oraz pionową oś y od minus czterech do sześciu. Na płaszczyźnie znajduje się prostokąt z wierzchołkami o współrzędnych : A początek nawiasu, 1, 1, zamknięcie nawiasu, B początek nawiasu, 7, 1, zamknięcie nawiasu, C początek nawiasu, 7, 5, zamknięcie nawiasu, D początek nawiasu, 1, 5, zamknięcie nawiasu. Na odcinku AB zaznaczony został punkt O, którego współrzędne to początek nawiasu, 4, 1, zamknięcie nawiasu. Na płaszczyźnie narysowano również koło, którego środek znajduje się w punkcie O, oraz którego brzeg przechodzi przez punkty D i C.

Minimalny promień koła o środku w punkcie $O = (4, 1)$ wynosi $5$ .

Słownik

koło o środku O i promieniu r

kołem o środku $O$ i promieniu $r$ nazywamy zbiór wszystkich punktów płaszczyzny, których odległość od punktu $O$ jest mniejsza lub równa $r$

Wprowadzenie

Animacja

Słownik