Przeczytaj

Przypomnijmy, że przesunięciem (translacją) o wektor $\vec{u}$ nazywamy przyporządkowanie każdemu punktowi $P$ płaszczyzny (przestrzeni) takiego punktu $P'$ , że:

\vec{P P'} = \vec{u}

R1Ur7Yate7tF4

Grafika przedstawia wektor oraz punkt przesunięty o ten wektor. Po prawej stronie grafiki znajduje się u→. Po lewej stronie znajduje się ten sam wektor, lecz na początku tego wektora znajduje się punkt P a na końcu punkt P prim.

Aby określić równanie obrazu okręgu w przesunięciu o wektor $\vec{u} = [p, q]$ wykorzystamy związki między współrzędnymi punktu i jego obrazu w przesunięciu o ten wektor.

Jeśli $\vec{u} = [p, q]$ to obrazem punktu $P = (x, y)$ jest taki punkt $P' = (x', y')$ , że $\vec{P P'} = \vec{u}$ , więc

\{\begin{cases} x' = x + p \\ y' = y + q \end{cases}

Napiszemy teraz równanie obrazu $K'$ okręgu $K$ o równaniu ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ w przesunięciu o wektorprzesunięcie (translacja) o wektorprzesunięciu o wektor $\vec{u} = [p, q]$ .

RfOoyOUOj8gcg

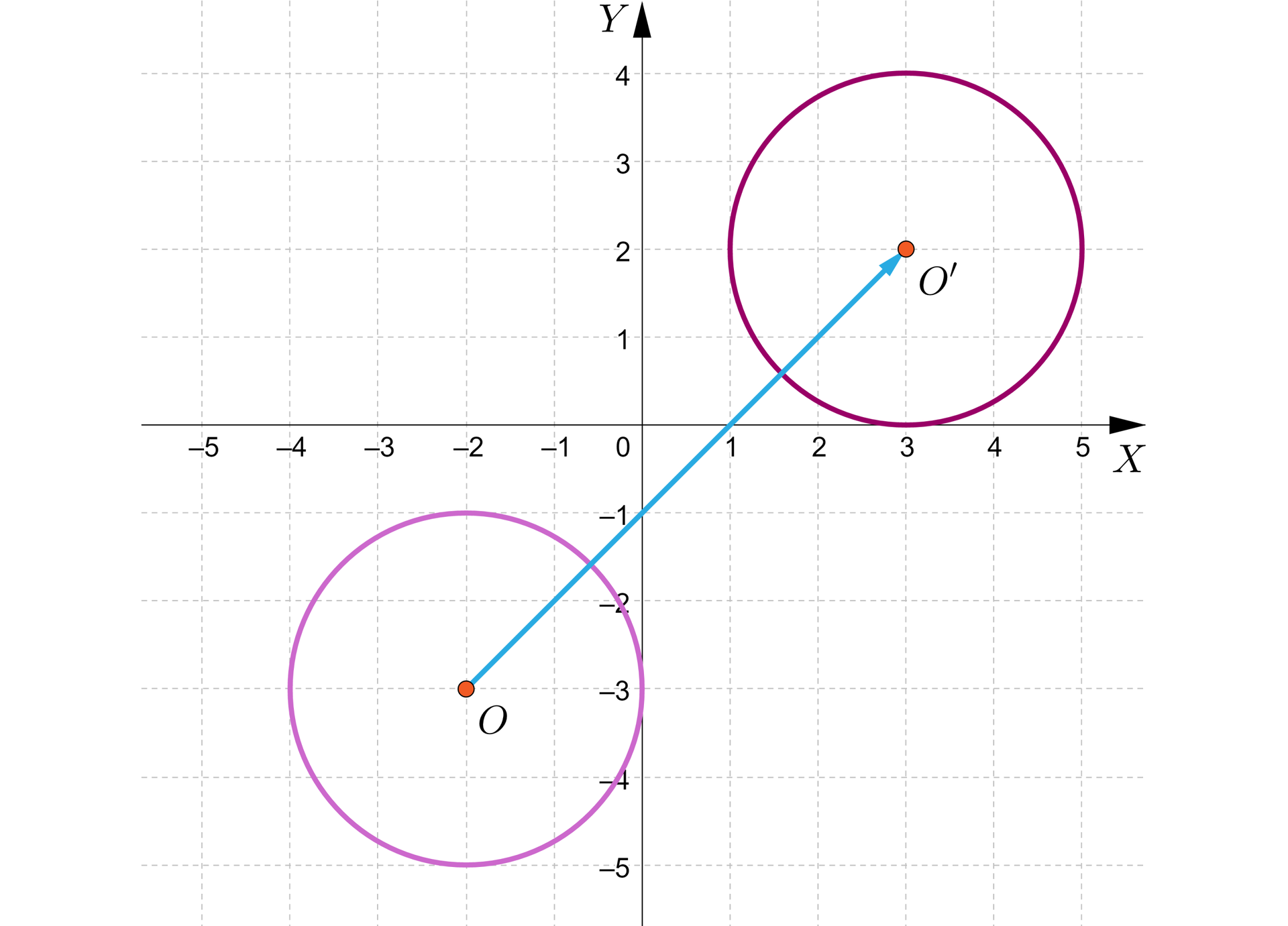
Grafika przedstawia układ współrzędnych z poziomą osią x od minus pięciu do pięciu i pionową osią y od minus pięciu do czterech. Na płaszczyźnie znajdują się dwa okręgi. Pierwszy z nich ma środek podpisany O w punkcie początek nawiasu, minus 2, minus 3, zamknięcie nawiasu, a długość jego promienia wynosi dwa. Drugi z nich ma środek O prim w punkcie początek nawiasu, 3, 2, zamknięcie nawiasu, a długość jego promienia wynosi dwa. Środki okręgów połączone są wektorem w taki sposób, że na początku wektora znajduje się środek okręgu O a na końcu oznaczonym strzałką znajduje się środek O prim.

Ponieważ przesunięcie o wektor jest izometriąizometriaizometrią, to obrazem okręgu jest okrąg o tym samym promieniu. Wykorzystamy związki między współrzędnymi punktu i jego obrazu w przesunięciu o wektor $\vec{u} = [p, q]$ :

\{\begin{cases} x = x' - p \\ y = y' - q \end{cases}

i podstawimy je do równania okręgu ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ .

Otrzymamy równanie jego obrazu w postaci ${(x' - p - a)}^{2} + {(y' - q - b)}^{2} = r^{2}$ .

Zapisując to równanie w postaci: ${(x' - (p + a))}^{2} + {(y' - (q + b))}^{2} = r^{2}$ , możemy wyciągnąć następujący wniosek:

Obrazem okręgu o równaniu ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ w przesunięciu o wektor $\vec{u} = [p, q]$ jest okrąg o równaniu

{(x - (p + a))}^{2} + {(y - (q + b))}^{2} = r^{2}

Środek tego okręgu ma współrzędne: $O' = (p + a, q + b)$ .

Przykład 1

Wyznaczymy równania obrazów okręgów o równaniach

a) ${(x - 3)}^{2} + {(y + 2)}^{2} = 36$ ,

b) $x^{2} + y^{2} - 12 x + 4 y + 15 = 0$ ,

w przesunięciu o wektor $\vec{u} = [2, 3]$ .

Rozwiązanie:

Ad a)

Okrąg o równaniu ${(x - 3)}^{2} + {(y + 2)}^{2} = 36$ ma środek w punkcie $(3, - 2)$ i promień długości $r = 6$ .

Obraz środka tego okręgu jest punktem, którego współrzędne są równe:

$a' = 3 + 2 = 5$ oraz $b' = - 2 + 3 = 1$ .

Zatem równanie obrazu okręgu ma postać: ${(x - 5)}^{2} + {(y - 1)}^{2} = 36$ .

Ad b)

Aby wyznaczyć równanie obrazu okręgu $x^{2} + y^{2} - 12 x + 4 y + 15 = 0$ , określimy współrzędne środka tego okręgu.

W tym celu przekształcamy jego równanie następująco:

$x^{2} - 12 x + 36 - 36 + y^{2} + 4 y + 4 - 4 + 15 = 0$

${(x - 6)}^{2} + {(y + 2)}^{2} = 25$ .

Okrąg o równaniu ${(x - 6)}^{2} + {(y + 2)}^{2} = 25$ ma środek w punkcie $(6, - 2)$ i promień długości $r = 5$ .

Obraz środka tego okręgu jest punktem o współrzędnych

$a' = 6 + 2 = 8$ oraz $b' = - 2 + 3 = 1$ .

Równanie obrazu okręgu ma postać: ${(x - 8)}^{2} + {(y - 1)}^{2} = 25$ .

Przykład 2

Okrąg o równaniu ${(x - 1)}^{2} + {(y - 3)}^{2} = 100$ przesunięto o wektor $\vec{u} = [12, q]$ .

Wyznaczymy wartość $q$ , dla której okrąg i jego obraz są styczne zewnętrznie.

Rozwiązanie:

Okrąg o równaniu ${(x - 1)}^{2} + {(y - 3)}^{2} = 100$ ma środek w punkcie $O = (1, 3)$ i promień długości $r = 10$ .

Obraz tego okręgu ma równanie ${(x - a')}^{2} + {(y - b')}^{2} = 100$ .

Współrzędne środka $O'$ okręgu będącego obrazem okręgu o środku $O = (1, 3)$ obliczymy w oparciu o wzory $a' = a + p$ i $b' = b + q$ , czyli dla $a = 1$ , $b = 3$ i $\vec{u} = [12, q]$ otrzymujemy

$a' = 1 + 12 = 13$ i $b' = 3 + q$ .

Odległość między środkami okręgów $K$ i $K'$ jest równa długości wektora $\vec{u}$ .

Jeżeli $\vec{u} = [p, q]$ to długość wektora wyraża wzór: $|\vec{u}| = \sqrt{p^{2} + q^{2}}$ .

Ponieważ $\vec{u} = [12, q]$ to jego długość możemy zapisać następująco: $|\vec{u}| = \sqrt{12^{2} + q^{2}}$ .

Długość wektora $\vec{u}$ jest odległością między środkami obu okręgów: $|\vec{u}| = |O O'|$ , więc $|O O'| = \sqrt{12^{2} + q^{2}}$ .

Okręgi są styczne zewnętrznie, gdy odległość między ich środkami jest równa sumie długości ich promieni.

$|O O'| = r_{1} + r_{2}$ , stąd $|O O'| = 20$ .

Otrzymujemy równanie: $\sqrt{144 + q^{2}} = 20$ .

Podnosimy obie strony tego równania do kwadratu: $144 + q^{2} = 400$ , stąd: $q^{2} = 400 - 144 = 256$ .

Rozwiązaniami równania $q^{2} = 256$ są liczby $q_{1} = 16$ lub $q_{2} = - 16$ .

Okrąg i jego obraz są styczne zewnętrznie, gdy $q = 16$ lub $q = - 16$ .

Przykład 3

Okrąg $K'$ jest obrazem okręgu $K$ o równaniu ${(x - 8)}^{2} + {(y - 1)}^{2} = 25$ w przesunięciu o wektor $\vec{u} = [- 7, 1]$ . Napiszemy równania stycznych do okręgu $K$ poprowadzonych ze środka okręgu $K'$ .

Rozwiązanie:

Okrąg $K$ o równaniu ${(x - 8)}^{2} + {(y - 1)}^{2} = 25$ ma środek w punkcie $O = (8, 1)$ i promień długości $r = 5$ .

Okrąg $K'$ o równaniu ${(x - a')}^{2} + {(y - b')}^{2} = 25$ ma środek $O' = (a', b')$ i promień długości $r = 5$ .

Obliczamy współrzędne środka okręgu $K'$ : $a' = 8 + (- 7) = 1$ i $b' = 1 + 1 = 2$ .

Zatem $O' = (1, 2)$ .

Wykorzystamy wzór $d = \frac{|A x_{0} + B y_{0} + C|}{\sqrt{A^{2} + B^{2}}}$ na odległość punktu $(x_{0}, y_{0})$ od prostej $A x + B y + C = 0$ .

Zapiszemy równania stycznych w postaci $y = m x + n$ .

Styczne te przechodzą przez punkt $O' = (1, 2)$ , ich równania są więc postaci $y - 2 = m (x - 1)$ .

Aby skorzystać ze wzoru na odległość punktu od prostej równanie $y - 2 = m (x - 1)$ zapisujemy w postaci $m x - y + 2 - m = 0$ .

Ze wzoru na odległość punktu od prostej obliczamy odległość środka okręgu $O = (8, 1)$ od prostej o równaniu $m x - y + 2 - m = 0$ i otrzymujemy:

$d = \frac{|m \cdot 8 + (- 1) \cdot 1 + 2 - m|}{\sqrt{m^{2} + 1^{2}}} = \frac{|7 m + 1|}{\sqrt{m^{2} + 1}}$ .

Z warunku styczności okręgu i prostej: $d = r$ wynika, że $\frac{|7 m + 1|}{\sqrt{m^{2} + 1}} = 5$ .

Ponieważ dla każdego $m \in ℝ$ : $\sqrt{m^{2} + 1} \neq 0$ to równanie możemy pomnożyć stronami przez $\sqrt{m^{2} + 1}$ .

Otrzymujemy równanie $|7 m + 1| = 5 \sqrt{m^{2} + 1}$ .

Podnosimy obie strony równania do kwadratu:

${(|7 m + 1|)}^{2} = 25 (m^{2} + 1)$

czyli

$49 m^{2} + 14 m + 1 = 25 m^{2} + 25$ .

Ostatecznie otrzymujemy równanie kwadratowe postaci: $12 m^{2} + 7 m - 12 = 0$ .

Wyróżnik trójmianu kwadratowego wynosi: $∆ = 49 - 4 \cdot 12 \cdot (- 12) = 625$ , stąd $\sqrt{∆} = 25$ .

Rozwiązaniami tego równania są liczby:

$m_{1} = \frac{- 7 - 25}{2 \cdot 12} = \frac{- 32}{24} = - \frac{4}{3}$ lub $m_{2} = \frac{- 7 + 25}{2 \cdot 12} = \frac{18}{24} = \frac{3}{4}$ .

Po podstawieniu ich do równania $m x - y + 2 - m = 0$ otrzymujemy równania prostych

$- \frac{4}{3} x - y + 2 - (- \frac{4}{3}) = 0$ , czyli $- 4 x - 3 y + 10 = 0$

oraz

$\frac{3}{4} x - y + 2 - \frac{3}{4} = 0$ czyli $3 x - 4 y + 5 = 0$ .

Odpowiedź:

Styczne do okręgu $K$ poprowadzone ze środka okręgu $K'$ mają równania: $- 4 x - 3 y + 10 = 0$ lub $3 x - 4 y + 5 = 0$ .

Słownik

przesunięcie (translacja) o wektor

przesunięcie o wektor $\vec{u}$ to przyporządkowanie każdemu punktowi $P$ płaszczyzny (przestrzeni) takiego punktu $P'$ , że $\vec{P P'} = \vec{u}$

izometria

przekształcenie płaszczyzny, które zachowuje odległości między punktami

Wprowadzenie

Animacja

Słownik