Dany jest trójkąt, którego boki mają długości: $15$, $16$, $17$. Naszym zadaniem będzie wyznaczenie miar kątów tego trójkąta. Na początek przyjmijmy oznaczenia jak na rysunku.

R1B4MlmCaPFD3

Ilustracja przedstawia trójkąt $ABC$. Z wierzchołka $C$ upuszczono wysokość $h$ na podstawę $AB$ w punkcie $D$. Punkt $D$ dzieli podstawę na dwa odcinki: $p$, czyli $AD$ oraz $q$, czyli $DB$. Poszczególne boki nazwano od przeciwległych im wierzchołków i przypisano im długości. Bok $c$ to odcinek $AB$ od długości 16. Bok $a$ to odcinek $BC$ o długości 15, a bok $b$ to odcinek $CA$ o długości 17.

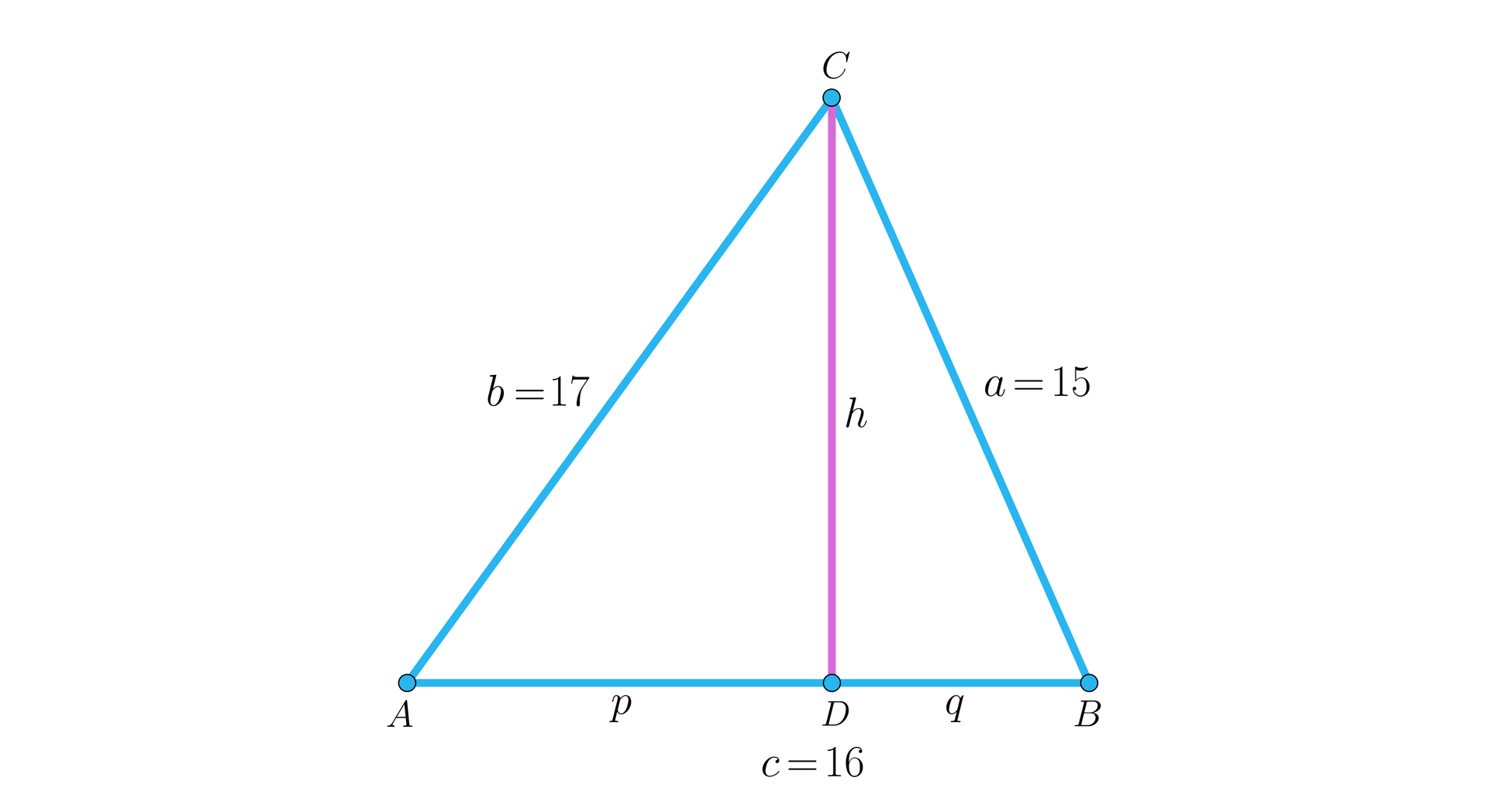
Korzystając z twierdzenia Pitagorasa odpowiednio dla trójkątów $ADC$ i $BDC$ mamy $p^2+h^2={17}^2$ oraz $q^2+h^2={15}^2$. Wiemy także, że $p+q=16$. Z pierwszych dwóch równań, eliminując niewiadomą $h$, otrzymujemy, że ${15}^2-q^2={17}^2-p^2$. Podstawiając teraz, że $q=16-p$, mamy ${15}^2-{\left(16-p\right)}^2={17}^2-p^2$. Upraszczając ostatnie równanie dostajemy, że $32p=320$. Stąd: $p=10$, $q=6$, $h=\sqrt{189}$. Zatem $\sin \alpha =\frac{\sqrt{189}}{17}\approx 0,8087$ oraz $\sin \beta =\frac{\sqrt{189}}{15}\approx 0,9165$. Przybliżone miary kątów są równe: $\alpha =54°$, $\beta =66°$ oraz $\gamma =60°$.

Rozważmy trójkąt, którego dwa boki mają długości: $\left|AB\right|=6$, $\left|AC\right|=8$, a kąt leżący między tymi bokami ma miarę $60°$. Te informacje w sposób jednoznaczny wyznaczają trójkąt, o czym mówi cecha $kbk$ przystawania trójkątów. Przypuśćmy jednak, że znamy także długość trzeciego boku tego trójkąta i jest ona równa $\left|BC\right|=2\sqrt{13}$. Naszym zadaniem jest wyznaczenie miar pozostałych kątów tego trójkąta.

Na wstępie zauważmy, że mając trzy dane boki trójkąta, moglibyśmy postąpić analogicznie do sposobu zastosowanego w Przykładzie 1., czyli rozwiązać układ trzech równań z trzema niewiadomymi, w którym dwa równania są stopnia drugiego. Znów uniknęlibyśmy stosowania twierdzenia sinusów, ale byłoby to nieracjonalne, bo jak za moment zobaczymy, twierdzenie sinusów „od razu” rozwiązuje nasz problem. Mamy bowiem $\frac{\left|BC\right|}{\sin 60°}=\frac{\left|AC\right|}{\sin \beta }=\frac{\left|AB\right|}{\sin \gamma }$. Stąd $\sin \beta =\frac{8·{\displaystyle \frac{\sqrt{3}}{2}}}{2\sqrt{13}}=\frac{2\sqrt{39}}{13}\approx 0,9608$ i $\beta \approx 74°$ oraz $\sin \gamma =\frac{6·{\displaystyle \frac{\sqrt{3}}{2}}}{2\sqrt{13}}=\frac{3\sqrt{39}}{26}\approx 0,7206$ i $\gamma \approx 46°$. Tym samym rozwiązanie problemu sprowadziło się do podstawienia wielkości do wzoru Snelliusa, krótko i elegancko.

Punkt $O$ jest ortocentrum trójkąta ostrokątnego $ABC$, w którym $\left|\measuredangle ABC\right|=60°$, $\left|AB\right|=10$, $\left|AC\right|=6\sqrt{3}$. Na trójkącie $ABO$ opisano okrąg. Odcinek $AO$ jest krótszą podstawą trapezu $ADBO$ wpisanego w okrąg. Oblicz miary kątów tego trapezu.

Rozwiązanie

Przyjmijmy oznaczenia takie, jak na rysunku. Punkty $P$ i $Q$ są spodkami odpowiednich wysokości.

R3SNr4u7USKbg

Ilustracja przedstawia trójkąt $ABC$ oparty na cięciwie $AB$. Większa część trójkąta leży poza okręgiem. Z wierzchołka $C$ linią przerywaną upuszczono wysokość na podstawę $AB$ w punkcie $P$. Wysokość przecina okrąg w punkcie $O$. Z wierzchołka $A$ linią przerywaną poprowadzono odcinek do punktu $O$. Z wierzchołka $B$ poprowadzono wysokość przechodzącą przez punkt $O$ do punktu $Q$ leżącego na boku $AC$ trójkąta. Na cięciwie $AB$ oparto też drugi trójkąt położony całkowicie w części płaszczyzny ograniczonej okręgiem. Jest to trójkąt $DBA$.

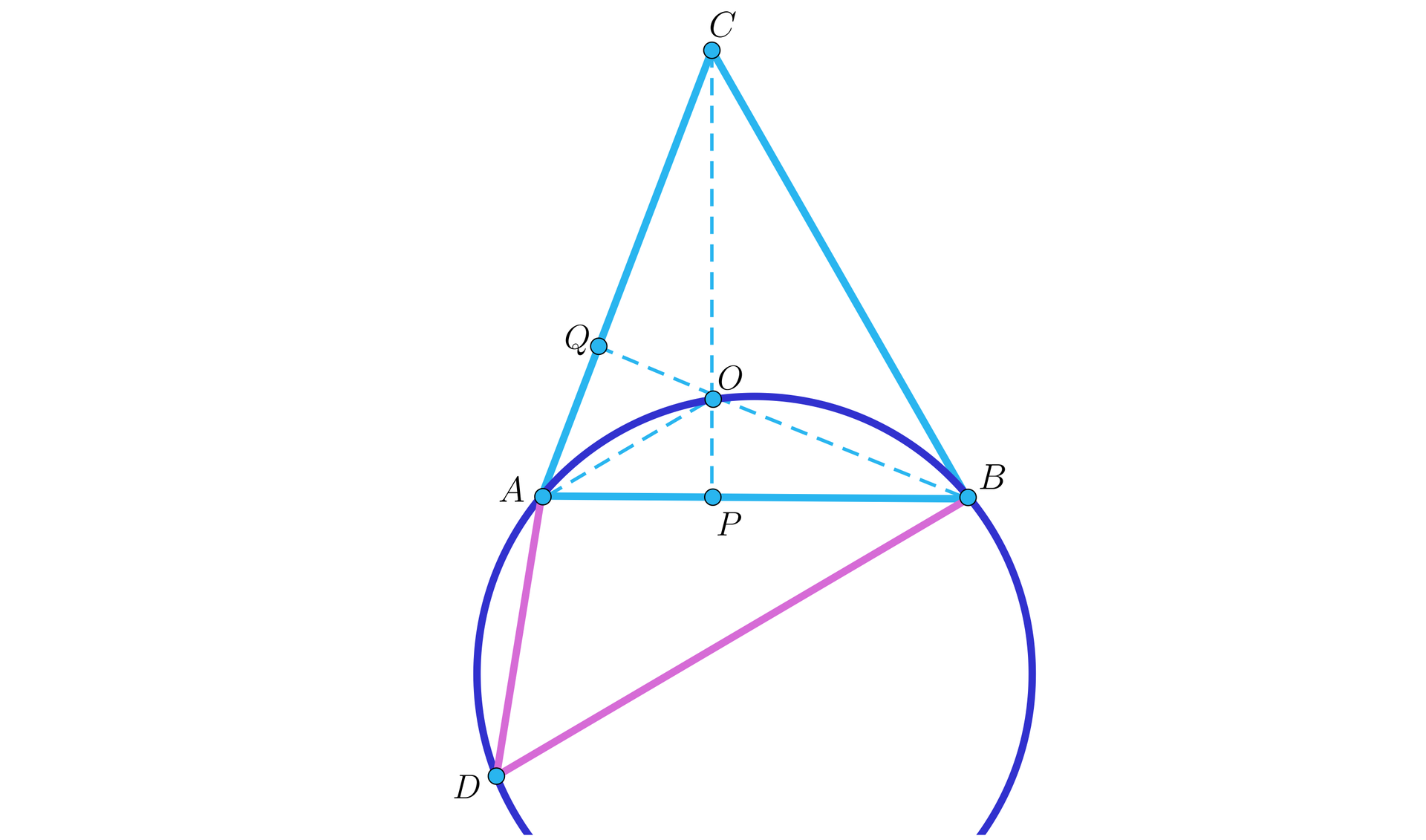
Oznaczmy kąty przy wierzchołkach $A$, $B$, $C$ odpowiednio przez $\alpha$, $\beta$, $\gamma$. Wtedy $\frac{\left|AB\right|}{\sin \gamma }=\frac{\left|AC\right|}{\sin \beta }$. Stąd $\sin \gamma =\frac{\left|AB\right|·\sin \beta }{\left|AC\right|}=\frac{10·{\displaystyle \frac{\sqrt{3}}{2}}}{6\sqrt{3}}=\frac{5}{6}$. Oznacza to, że $\gamma \approx 56°$. Z bilansu kątów w trójkącie otrzymujemy, że $\alpha \approx 64°$. Pozostaje zauważyć, że przy przyjętych oznaczeniach, kąt $AOB$ ma miarę $\left|\measuredangle AOB\right|=180°-(90°-\alpha )-(90°-\beta )=\alpha +\beta$ i jest to kąt rozwarty trapezu równoramiennego (co wynika z faktu, że jest on wpisany w okrąg). Zatem kąt rozwarty ma miarę w przybliżeniu równą $124°$, a kąt ostry tego trapezu ma miarę $56°$.

cechy przystawania trójkątów to warunki konieczne i wystarczające na to, by dwa trójkąty były przystające; najczęściej mówi się o cechach: $bbb$ (bok‑bok‑bok), $bkb$ (bok‑kąt‑bok); $kbk$ (kąt‑bok‑kąt)