Przeczytaj

Dwa okręgi mające dokładnie jeden punkt wspólny nazywamy stycznymi. Punkt wspólny nazywamy wówczas punktem styczności. Okręgi mogą być styczne zewnętrznie lub styczne wewnętrznie.

Przeanalizujemy sytuację, gdy okręgi są styczne wewnętrznie, czyli jeden okrąg leży wewnątrz koła ograniczonego drugim.

Dwa okręgi są styczne wewnętrzniedwa okręgi styczne wewnętrznieDwa okręgi są styczne wewnętrznie wtedy i tylko wtedy, gdy odległość środków okręgów jest równa różnicy promieni:

$|O_{1} O_{2}| = r_{2} - r_{1}$ , gdy $r_{2} > r_{1}$ .

Jest to warunek konieczny i wystarczający styczności wewnętrznej dwóch okręgów.

R1BhS0WsMypiZ

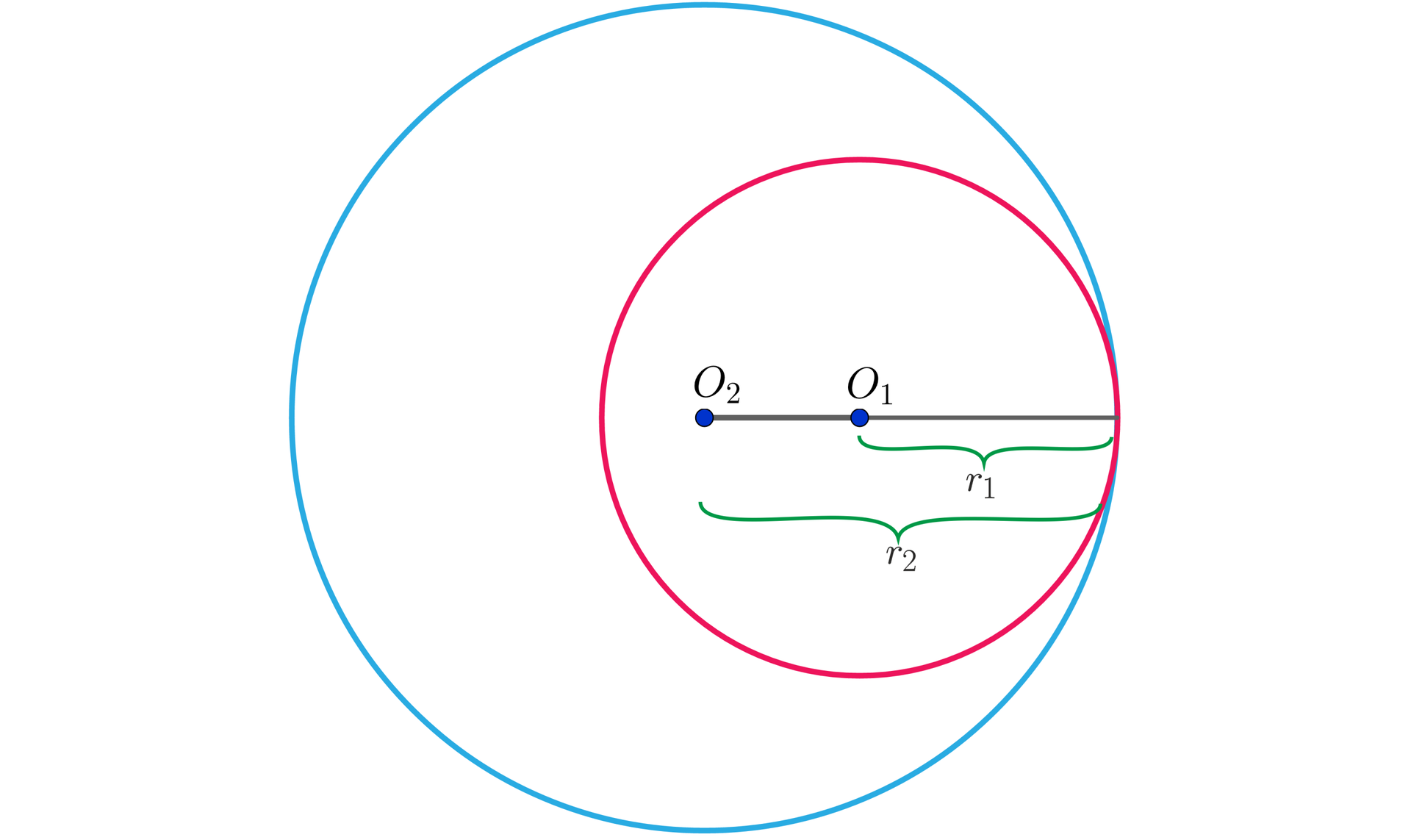
Grafika przedstawia dwa okręgi. Jeden okrąg znajduje się wewnątrz drugiego. Mniejszy okrąg o środku O1 i promieniu r1 znajduje się wewnątrz większego okręgu o środku O2 i promieniu r2. Mniejszy okrąg jest styczny do większego okręgu. Ze środka większego okręgu poprowadzono poziomy promień. Środek mniejszego okręgu leży na tym promieniu, a promień mniejszego okręgu zawiera się promieniu okręgu większego.

Rozważmy dwa okręgi o środkachokrąg o środku $O$ i promieniu $r$ okręgi o środkach $O_{1} = (a_{1}, b_{1})$ i promieniuokrąg o środku $O$ i promieniu $r$ i promieniu $r_{1}$ oraz $O_{2} = (a_{2}, b_{2})$ i promieniu $r_{2}$ . Jeżeli mamy dwa okręgi o równaniach ${(x - a_{1})}^{2} + {(y - b_{1})}^{2} = {r_{1}}^{2}$ i ${(x - a_{2})}^{2} + {(y - b_{2})}^{2} = {r_{2}}^{2}$ , to są one stycznie wewnętrznie, gdy $|O_{1} O_{2}| = \sqrt{{(a_{2} - a_{1})}^{2} + {(b_{2} - b_{1})}^{2}} = |r_{2} - r_{1}|$ .

Odległość dwóch punktów jest zawsze liczbą nieujemną; ponieważ nie możemy stwierdzić, która z danych liczb $r_{1}$ czy $r_{2}$ jest większa, zapisaliśmy różnicę promieni w wartości bezwzględnej.

Skorzystaliśmy ze wzoru na odległość dwóch punktów $|A B| = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$ .

Przykład 1

Sprawdzimy, czy okręgi o promieniach $r_{1} = 7$ , $r_{2} = 2$ , których odległość między środkami wynosi $5$ , są styczne wewnętrznie.

Rozwiązanie

Okręgi o promieniach $r_{1} = 7$ , $r_{2} = 2$ , których odległość między środkami wynosi $5$ , są styczne wewnętrznie bo $5 = 7 - 2$ , czyli zachodzi warunek konieczny i wystarczający styczności wewnętrznej dwóch okręgów $|O_{1} O_{2}| = r_{1} - r_{2}$ .

Przykład 2

Sprawdzimy, czy okręgi ${(x - 1)}^{2} + {(y + 2)}^{2} = 25$ i ${(x + 2)}^{2} + {(y - 2)}^{2} = 4$ są styczne wewnętrznie.

Rozwiązanie

Okrąg o równaniu ${(x - 1)}^{2} + {(y + 2)}^{2} = 25$ ma środek w punkcie $O_{1} = (1, - 2)$ i promień $r_{1} = 5$ .

Okrąg o równaniu ${(x + 2)}^{2} + {(y - 2)}^{2} = 4$ ma środek w punkcie $O_{2} = (- 2, 2)$ i promień $r_{2} = 2$ .

Obliczamy odległość środków $O_{1} O_{2}$ tych okręgów ze wzoru $|A B| = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$ :

$|O_{1} O_{2}| = \sqrt{(- 2 - 1)^{2} + (2 - (- 2))^{2}} = \sqrt{3^{2} + 4^{2}} = \sqrt{25} = 5$ .

Sprawdzamy warunek $|O_{1} O_{2}| = |r_{2} - r_{1}|$ i widzimy, że dla $|O_{1} O_{2}| = 5$ , $r_{1} = 5$ i $r_{2} = 2$ nie jest on spełniony bo $5 \neq |2 - 5| = 3$ .

Przykład 3

Wyznaczymy długość promienia okręgu o środku w punkcie $(- 1, - 1)$ tak, aby był on styczny wewnętrznie do okręgu ${(x - 5)}^{2} + {(y - 7)}^{2} = 16$ . Obliczymy współrzędne punktu styczności.

Rozwiązanie

Okrąg o równaniu ${(x - 5)}^{2} + {(y - 7)}^{2} = 16$ ma środek w punkcie $O_{1} = (5, 7)$ i promień $r_{1} = 4$ .

Okrąg o równaniu ${(x + 1)}^{2} + {(y + 1)}^{2} = r_{2}$ ma środek w punkcie $O_{2} = (- 1, - 1)$ i promień $r_{2}$ .

Aby okręgi były styczne wewnętrzniedwa okręgi styczne wewnętrznieokręgi były styczne wewnętrznie, musi być spełniony warunek $|O_{1} O_{2}| = |r_{2} - r_{1}|$ .

Ponieważ $|O_{1} O_{2}| = \sqrt{{(- 1 - 5)}^{2} + {(- 1 - 7)}^{2}} = \sqrt{{(- 6)}^{2} + {(- 8)}^{2}} = \sqrt{100} = 10$ i $r_{1} = 4$ , to otrzymujemy równanie $10 = |r_{2} - 4|$ , co daje $10 = r_{2} - 4$ lub $- 10 = r_{2} - 4$ .

Ponieważ $r_{2} > 0$ , to $r_{2} = 14$ .

Aby znaleźć punkt wspólny okręgów, rozwiązujemy układ złożony z równań obu okręgów.

W tym celu zapisujemy równania w postaci:

$\{\begin{cases} {(x - 5)}^{2} + {(y - 7)}^{2} = 16 \\ {(x + 1)}^{2} + {(y + 1)}^{2} = 196 \end{cases}$

$\{\begin{cases} x^{2} - 10 x + 25 + y^{2} - 14 y + 49 = 16 \\ x^{2} + 2 x + 1 + y^{2} + 2 y + 1 = 196 \end{cases}$

$\{\begin{cases} x^{2} + y^{2} - 10 x - 14 y + 74 = 16 (1) \\ x^{2} + y^{2} + 2 x + 2 y + 2 = 196 (2) \end{cases}$ .

Odejmujemy stronami od równania $(1)$ równanie $(2)$ i otrzymujemy

$12 x + 16 y - 72 = 180$

$12 x + 16 y = 252$ , wyznaczamy z tego równania $x$ :

$12 x = 252 - 16 y$ więc $x = 21 - \frac{4}{3} y$ .

Podstawiamy $x = 21 - \frac{4}{3} y$ do np. pierwszego równania, otrzymując ${(21 - \frac{4}{3} y)}^{2} + y^{2} + 2 (21 - \frac{4}{3} y) + 2 y = 194$ .

Dokonujemy przekształceń: $441 - \frac{168}{3} y + \frac{16}{9} y^{2} + y^{2} + 42 - \frac{8}{3} y + 2 y - 194 = 0$

i po redukcji dochodzimy do równania kwadratowego $\frac{25}{9} y^{2} - \frac{170}{3} y + 289 = 0$ .

Wyróżnik tego trójmianu wynosi $Δ = {(\frac{170}{3})}^{2} - 4 \cdot 289 \cdot \frac{25}{9} = 0$ .

Równanie $\frac{25}{9} y^{2} - \frac{170}{3} y + 289 = 0$ ma jedno rozwiązanie $y_{0} = - \frac{\frac{- 170}{3}}{2 \cdot \frac{25}{9}} = \frac{\frac{170}{3}}{\frac{50}{9}} = \frac{51}{5}$ .

Do równania $x = 21 - \frac{4}{3} y$ podstawiamy $y = \frac{51}{5}$ :

$x = 21 - \frac{4}{3} \cdot \frac{51}{5} = \frac{37}{5}$ .

Ilustracja sytuacji przedstawionej w zadaniu.

R1bIkwLjs8UMN

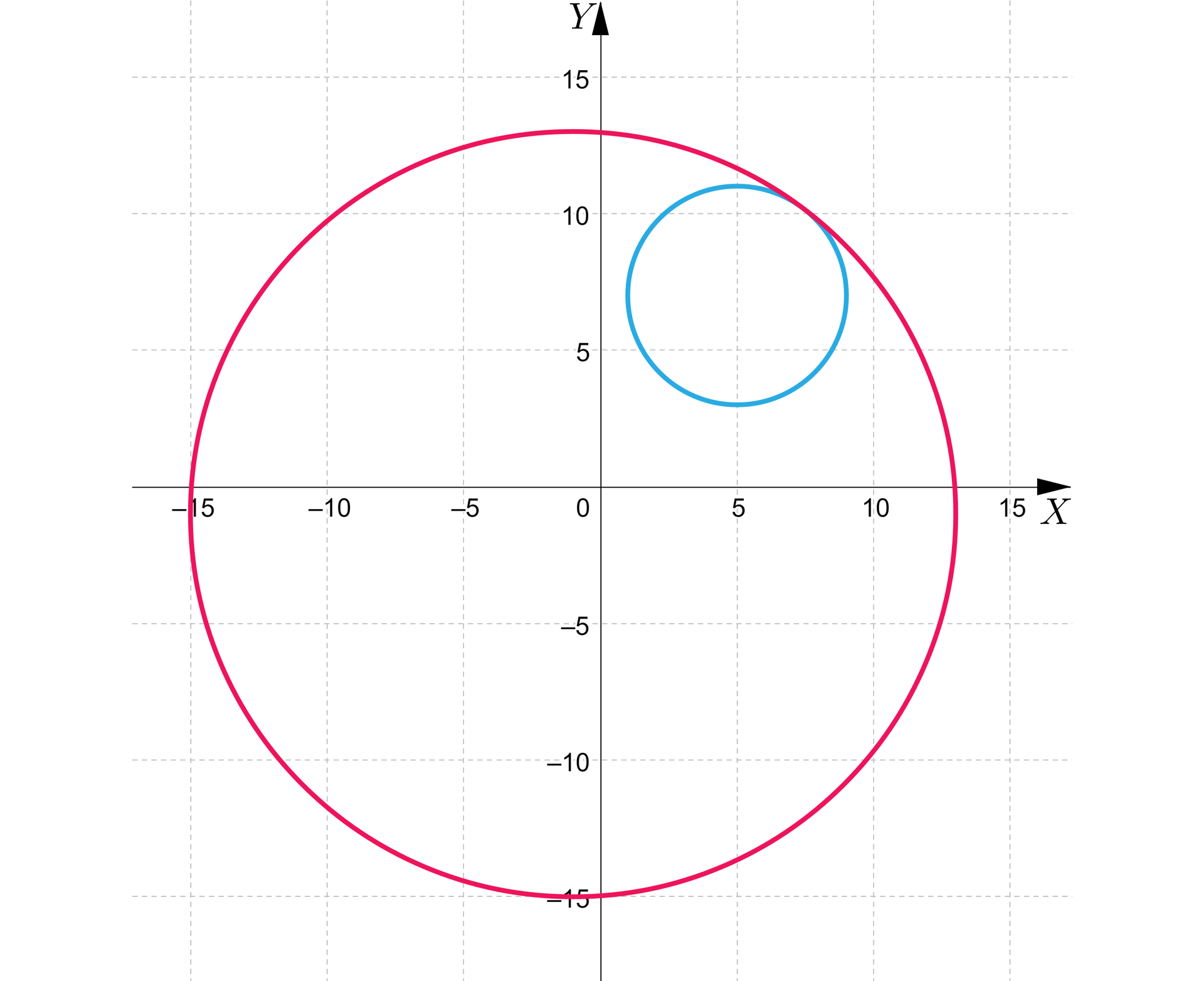
Grafika przedstawia układ współrzędnych z poziomą osią x od minus piętnastu do piętnastu z podziałką co pięć i pionową osią y od minus piętnastu do piętnastu również z podziałką co pięć. Na płaszczyźnie znajdują się dwa okręgi. Pierwszy, większy okrąg przechodzi przez punkty początek nawiasu, minus 15, 0, zamknięcie nawiasu, początek nawiasu, 0, minus 15, zamknięcie nawiasu, początek nawisu, minus 10, 10, zamknięcie nawiasu. Drugi okrąg znajduje się wewnątrz pierwszego i jest styczny do pierwszego okręgu i znajduje się w całości w pierwszej ćwiartce.

Promień okręgu o środku w punkcie $(- 1, - 1)$ wynosi $14$ , wtedy jest on styczny wewnętrznie do okręgu ${(x - 5)}^{2} + (y - 7)^{2} = 16$ . Współrzędne punktu styczności wynoszą $(\frac{37}{5}, \frac{51}{5})$ .

Przykład 4

Wyznaczymy współrzędne środka okręgu o promieniu $1$ przechodzącego przez punkt $(4, 0)$ i stycznego wewnętrznie do okręgu $x^{2} + y^{2} + 8 x - 84 = 0$ .

Rozwiązanie

Równanie okręgu doprowadzamy do postaci ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ .

$x^{2} + y^{2} + 8 x - 84 = 0$

$x^{2} + 8 x + 16 - 16 + y^{2} - 84 = 0$

${(x + 4)}^{2} - 16 + y^{2} - 84 = 0$ ,

${(x + 4)}^{2} + y^{2} = 10^{2}$

Stąd wnioskujemy, że środkiem okręgu jest punkt $O = (- 4, 0)$ a promień ma długość $10$ .

Punkt $(4, 0)$ oznaczmy przez $S$ . Wiemy, że $r = 1$ .

Szukany okrąg ma spełniać dwa warunki:

ma przechodzić przez punkt $S = (4, 0)$ $(1)$ ,
ma być styczny wewnętrznie do danego okręgu $(2)$ .

Z warunku $(1)$ : ${(4 - a)}^{2} + b^{2} = 1$

Z warunku $(2)$ : $10 - 1 = 9$ .

Zatem $|O S| = 9$ , $O = (- 4, 0)$ i $S = (a, b)$ , więc ${|O S|}^{2} = {(a + 4)}^{2} + b^{2}$ , czyli ${(a + 4)}^{2} + b^{2} = 9^{2}$ .

Otrzymujemy zatem układ równań:

$\{\begin{cases} {(4 - a)}^{2} + b^{2} = 1 (1) \\ {(a + 4)}^{2} + b^{2} = 81 (2) \end{cases}$ .

Odejmujemy stronami od równania $(2)$ równanie $(1)$ i otrzymujemy ${(a + 4)}^{2} - {(4 - a)}^{2} = 80$ .

Po przekształceniach:

$16 + 8 a + a^{2} - (16 - 8 a + a^{2}) = 80$

$16 + 8 a + a^{2} - 16 + 8 a - a^{2} = 80$

ostatecznie mamy

$16 a = 80$

$a = \frac{80}{16} = 5$ .

Podstawmy $a = 5$ do równania $(1)$ :

${(4 - 5)}^{2} + b^{2} = 1$ , $b^{2} = 0$ otrzymujemy $b = 0$ .

Poszukiwany okrąg ma środek w punkcie $S = (5, 0)$ .

R9sGB5d5YePCI

Grafika przedstawia układ współrzędnych z poziomą osią x od minus czternastu do sześciu z podziałką co dwa i pionową osią y od minus dziesięciu do dziesięciu również z podziałką co dwa. Na płaszczyźnie znajdują się dwa okręgi. Pierwszy, większy okrąg ma środek w punkcie O, którego współrzędne to początek nawiasu, minus 4, 0, zamknięcie nawiasu, okrąg ten ma promień o długości dziesięć. Drugi okrąg znajduje się wewnątrz pierwszego, jego środek podpisany jest literą S. Okrąg ten przechodzi przez punkt A o współrzędnych początek nawiasu, 4, 0, zamknięcie nawiasu oraz punkt początek nawiasu, 6, 0, zamknięcie nawiasu, który jest punktem wspólnym obu okręgów.

Słownik

okrąg o środku

O

i promieniu

r

okrąg o środku

O

i promieniu

r

zbiór wszystkich punktów $P$ płaszczyzny, których odległość od punktu $O$ jest równa $r$

dwa okręgi styczne wewnętrznie

dwa okręgi są styczne wewnętrznie, gdy odległość środków tych okręgów jest równa różnicy promieni

Wprowadzenie

Animacja

Słownik