Przeczytaj

Wielościan wypukły

Wielościanem nazywamy bryłę, której wszystkie ściany są wielokątami i spełnione są warunki:

Każde dwie ściany mają wspólną krawędź, wierzchołek lub nie mają części wspólnej.
Każda krawędź jest wspólna dla dokładnie dwóch ścian.
Każdy wierzchołek jest wspólny dla co najmniej trzech ścian.

Wielościan nazywamy wypukłym, gdy w całości leży po jednej ze stron płaszczyzn wyznaczonych przez każdą ze ścian.

Przykład 1

Ocenimy, czy wielościany poniżej są wypukłe.

ROK6ehFFOQGFe

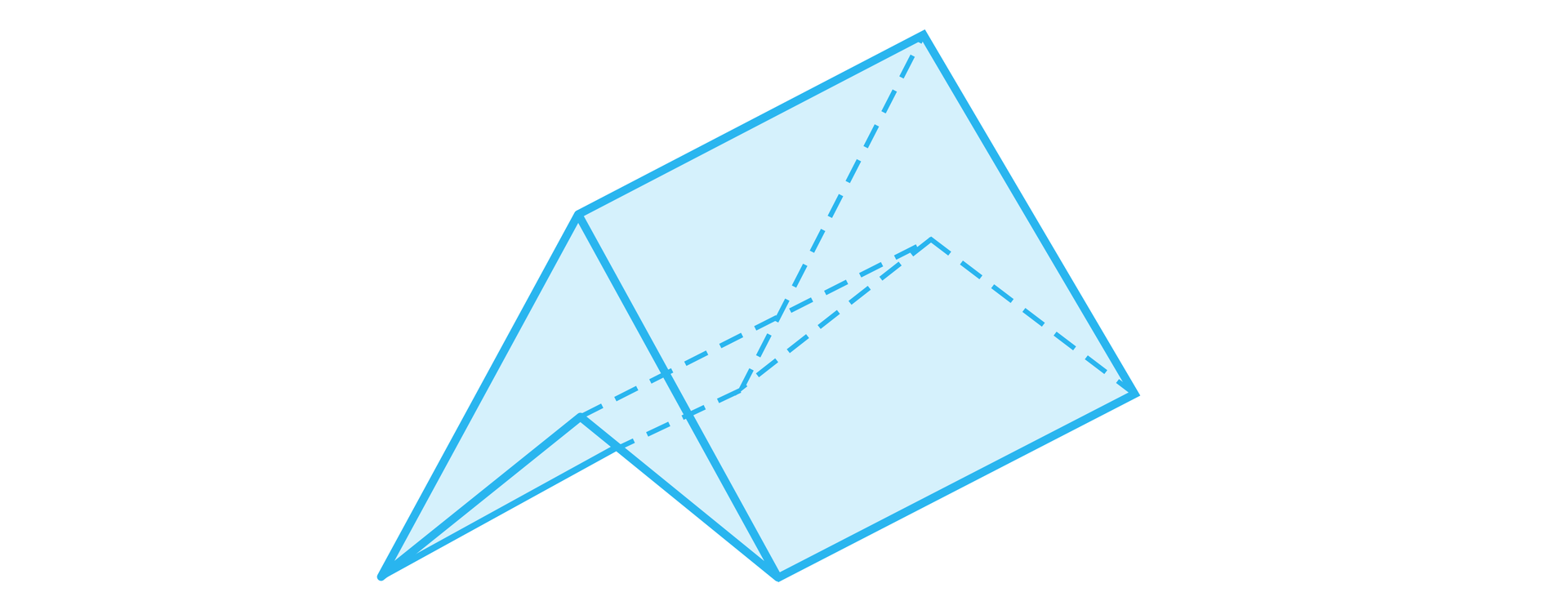
Ilustracja przedstawia model graniastosłupa o podstawie czworokąta wklęsłego w kształcie litery V.

Nie jest to wielościan wypukły.

RtZ81dONS0aWu

Ilustracja przedstawia model dwudziestościanu foremnego, którego ścianami są trójkąty równoboczne. Bryła przypomina oszlifowany kamień lub dwudziestościenną kostkę do gry..

Jest to wielościan wypukływielościan wypukływielościan wypukły.

Ważne!

Z przykładu powyżej wynika, że nie każdy graniastosłup jest wielościanem wypukłym.

Liczba wierzchołków, krawędzi i ścian w wielościanach

Oznaczmy przez $W$ – liczbę wierzchołków, przez $S$ – liczbę ścian i przez $K$ – liczbę krawędzi wielościanu.

Przykład 2

Pokażemy, że liczby $W$ , $K$ i $S$ nie są przypisane do jednego konkretnego wielościanu.

RJIc1JPahGMu6

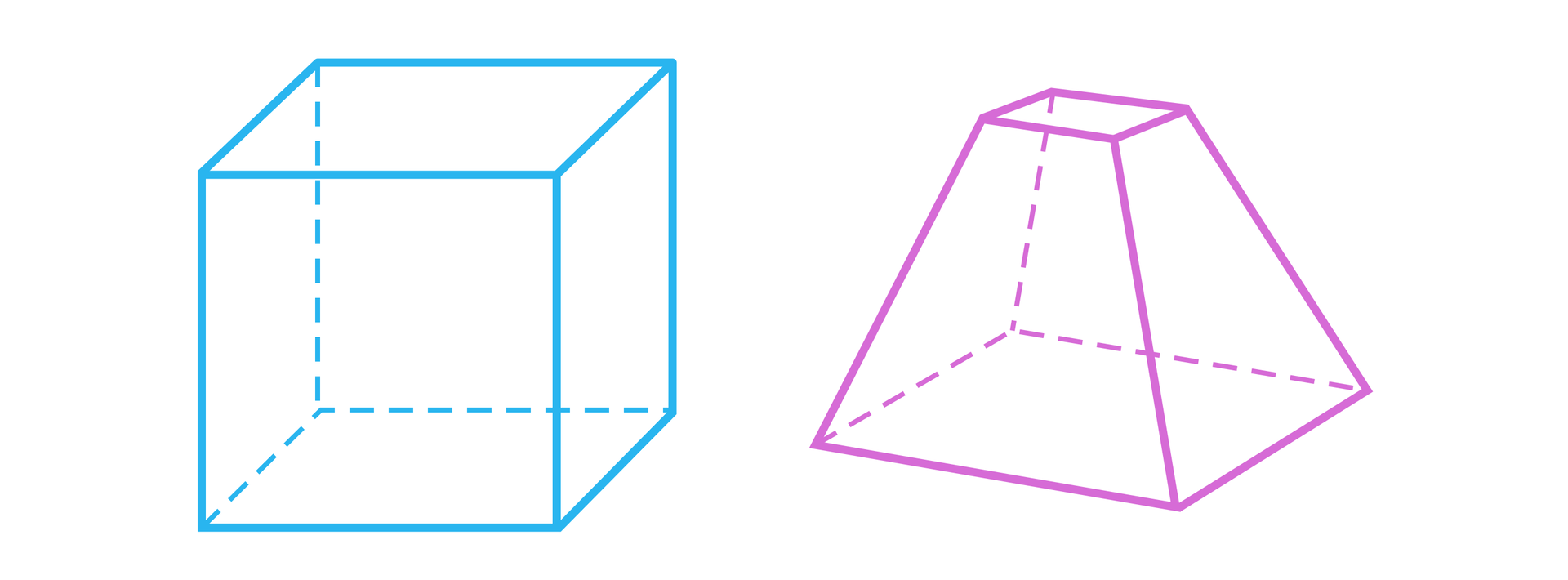
Ilustracja przedstawia dwie figury geometryczne. Pierwsza figura to sześcian. Druga figura to ostrosłup ścięty czworokątny.

Rozwiązanie

Rozważymy sześcian i ostrosłup ścięty czworokątny.

Dla obu tych brył mamy $W = 8$ , $S = 6$ i $K = 12$ .

Zastanówmy się jakimi liczbami mogą być $W$ , $K$ i $S$ .

Przykład 3

Pokażemy, że liczba krawędzi wielościanów może być każdą liczbą parzystą nie mniejszą od $6$ .

Rozwiązanie

Jeżeli wielościanwielościanwielościan składa się z samych trójkątów, to najmniejsza liczba krawędzi jaką możemy otrzymać to $6$ (w przypadku ostrosłupa trójkątnego) i to jest najmniejsza liczba krawędzi, jaka może być. Dla każdej liczby parzystej $n$ od $6$ wzwyż mamy taki wielościan – jest to np. ostrosłup $\frac{n}{2}$ –kątny.

Przykład 4

Pokażemy, że liczba krawędzi wielościanu może być każdą liczbą nieparzystą nie mniejszą od $9$ .

Rozwiązanie

W poprzednim przykładzie wykazaliśmy, że każda liczba parzysta większa od $4$ może być liczbą krawędzi wielościanu. Powiedzieliśmy, że przykładem wielościanu o parzystej liczbie krawędzi jest ostrosłup.

Weźmy więc ostrosłup z odciętym jednym z wierzchołków przy podstawie.

Ostrosłup ze ściętym wierzchołkiem przy podstawie będzie miał o $3$ krawędzie więcej niż miałby ostrosłup. Dla ostrosłupa trójkątnego po ścięciu wierzchołka będziemy mieć $9$ krawędzi.

R1e8foNL57bR6

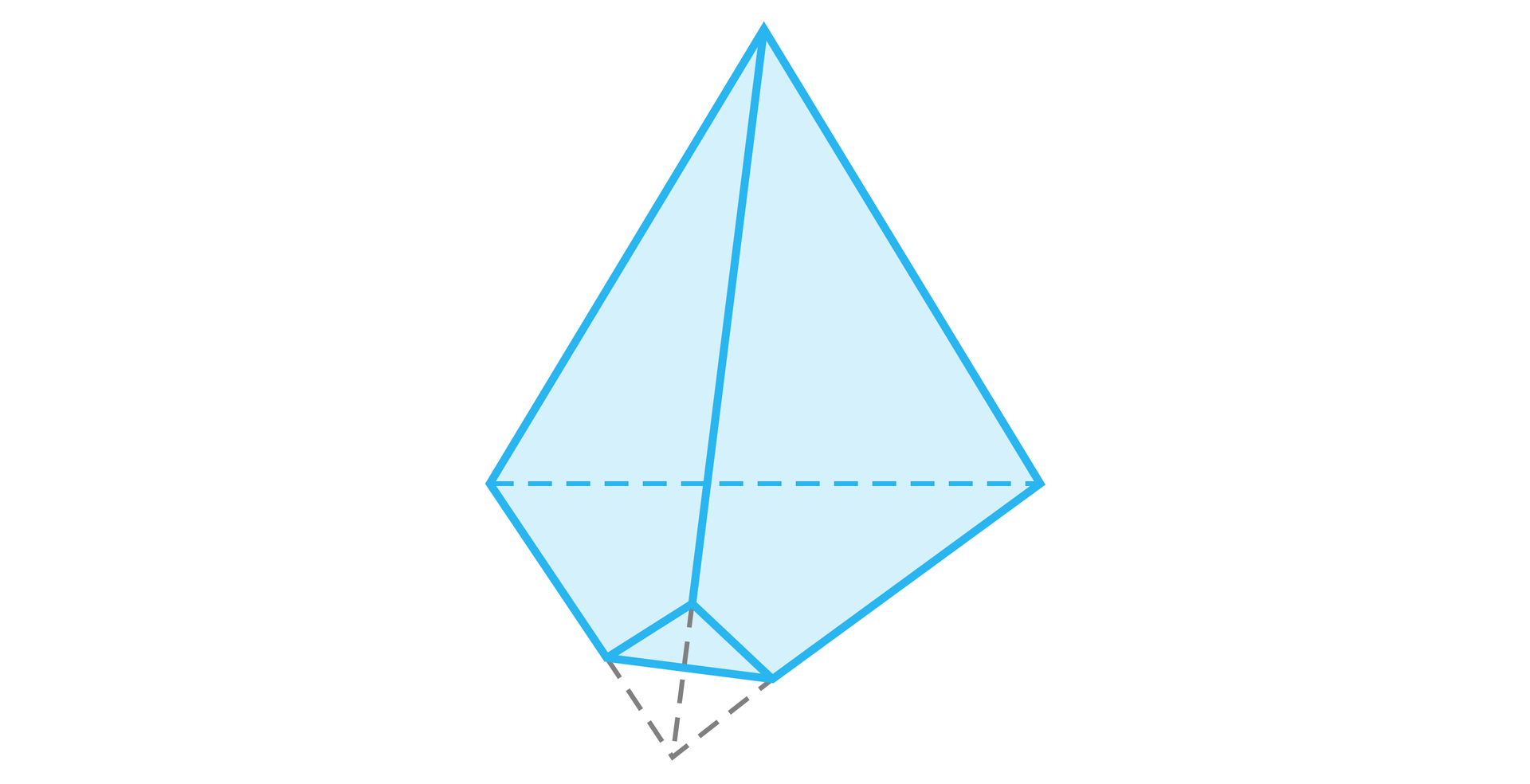
Ilustracja przedstawia ostrosłup trójkątny. Odcięto jeden z jego wierzchołków przy podstawie. Liniami przerywanymi zaznaczono krawędzie odciętej figury.

Dla czworokątnego będzie to $11$ krawędzi itd. A zatem będziemy mieć wielościan o liczbie krawędzi będącej każdą liczbą nieparzystą większą lub równą $9$ .

Ważne!

$W \geq 4$ i $S \geq 4$
Wiemy, że trzy punkty w przestrzeni wyznaczają dokładnie jedną płaszczyznę. A zatem, żeby powstał wielościanwielościanwielościan $W \geq 4$ , a z tego wynika, że również $S \geq 4$ .
$3 S \leq 2 K$
Jest tak, ponieważ każda krawędź jest wspólna dla dwóch ścian, a ściany są wielokątami (czyli należą do nich co najmniej trzy krawędzie).
$3 W \leq 2 K$
Jest tak, ponieważ każda krawędź łączy dwa wierzchołki, a z każdego wierzchołka wychodzą co najmniej trzy krawędzie.

Twierdzenie Eulera

Twierdzenie Eulera dla wielościanów wypukłych określa zależność pomiędzy liczbą ścian, krawędzi i wierzchołków wielościanu wypukłego.

Twierdzenie Eulera

Twierdzenie: Twierdzenie Eulera

Niech będzie dany wielościan wypukły. Wówczas:

W + S - K = 2

Dowód twierdzenia Eulera opiera się o analizę diagramu Schlegela.

Wniosek:

Z uwagi powyżej mamy, że $3 S \leq 2 K$ , czyli $S \leq \frac{2}{3} K$ .

A zatem z twierdzenia Eulera dla wielościanów wypukłych mamy $2 = W + S - K \leq W + \frac{2}{3} K - K$ .

A stąd $W \geq 2 + \frac{1}{3} K$ . Analogicznie $S \geq 2 + \frac{1}{3} K$ .

Przykład 5

Sprawdzimy, czy wielościan wypukływielościan wypukływielościan wypukły może mieć $7$ krawędzi.

Rozwiązanie

Mamy $K = 7$ , a to oznacza z twierdzenia Eulera, że $W + S = 9$ . Mamy $W \geq 4$ i $S \geq 4$ .

Możemy mieć więc:

$W = 4$ i $S = 5$ lub
$W = 5$ i $S = 4$ .

Jedynym wielościanem wypukłym, który ma $4$ wierzchołki lub $4$ krawędzie jest ostrosłup trójkątny, ale wtedy liczba drugiego typu elementów nie może wynosić $5$ .

A zatem wielościan wypukły nie może mieć $7$ krawędzi.

Ważne!

Żaden wielościan nie ma siedmiu krawędzi. Liczba krawędzi wielościanu może wynosić $6$ (w przypadku ostrosłupa trójkątnego) lub być dowolną liczbą całkowitą większą od $7$ .

Uwaga:

Dla niektórych wielościanów, które nie są wypukłe wzór Eulera również zadziała.

Przykład 6

Rozważymy graniastosłup przedstawiony na rysunku. Sprawdzimy, czy zachodzi dla niego twierdzenie Eulera.

RtatX6NlbOnD7

Ilustracja przedstawia model graniastosłupa o podstawie czworokąta wklęsłego o podstawie w kształcie litery V.

Rozwiązanie

Dla tego wielościanu mamy $W = 8$ , $K = 12$ , $S = 6$ .

Zauważmy, że $W + S - K = 8 + 6 - 12 = 2$ .

Przykład 7

Rozważymy wielościanwielościanwielościan powstały przez sklejenie krawędzią dwóch ostrosłupów czworokątnych. Sprawdzimy, czy zachodzi dla niego twierdzenie Eulera.

R43qP6M01Vc1y

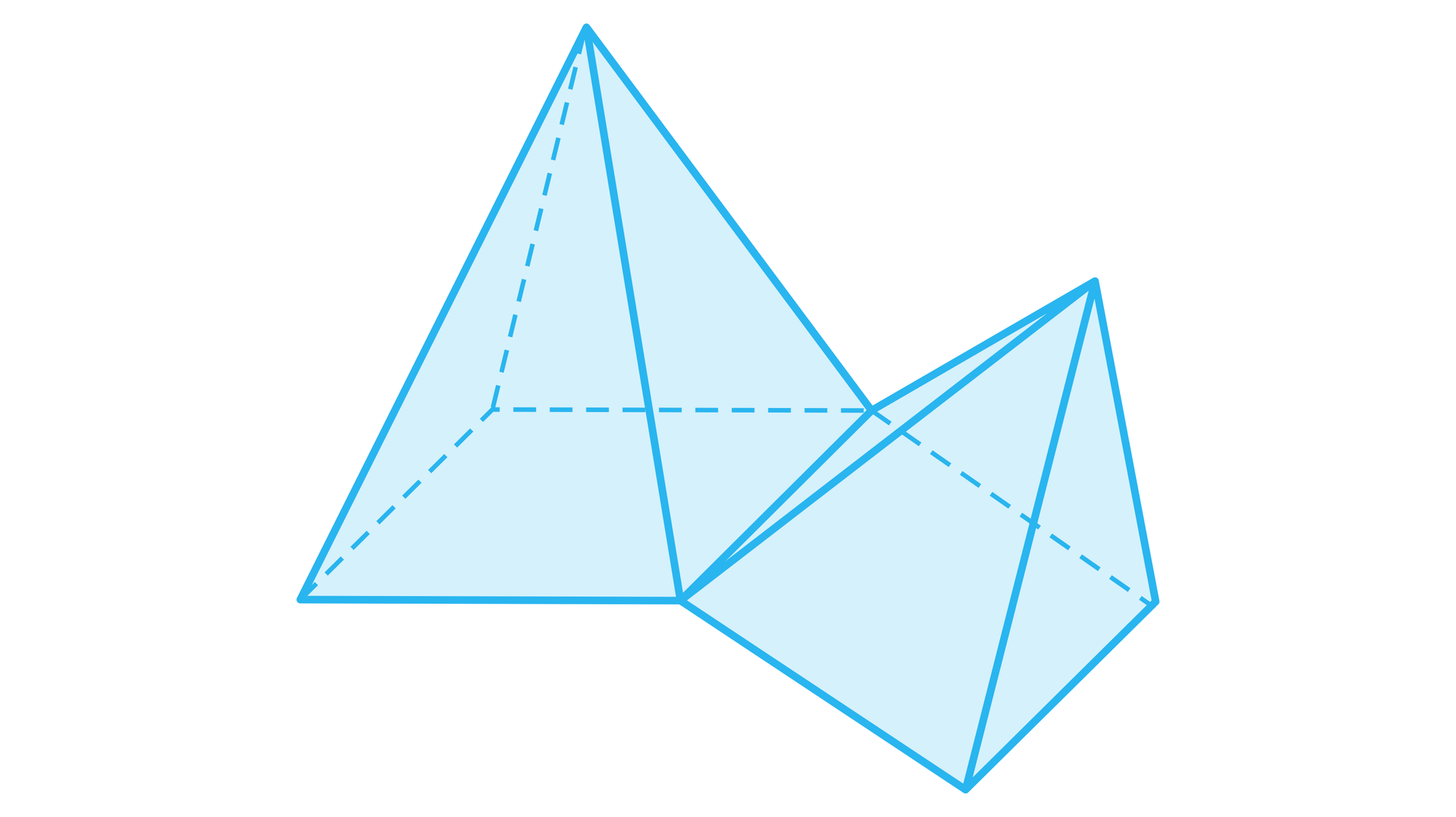
Ilustracja przedstawia dwa ostrosłupy czworokątne. Zostały one połączone jedną krawędzią podstawy. Ich podstawy nie leżą na jednej płaszczyźnie.

Rozwiązanie

Mamy $W = 8$ , $K = 15$ , $S = 10$ .

Zauważmy, że $W + S - K = 8 + 10 - 15 = 3 \neq 2$ .

Twierdzenie Eulera, a graniastosłupy

Wiemy, że nie każdy graniastosłup jest wielościanem wypukłym. Nie możemy więc bezpośrednio korzystać z twierdzenia Eulera.

Rozważymy graniastosłup o podstawie $n$ –kąta.

Taki graniastosłup będzie miał po $n$ wierzchołków w każdej podstawie, czyli $W = 2 n$ .

Będzie miał $n$ –krawędzi w każdej podstawie i $n$ krawędzi bocznych, czyli $K = n + n + n = 3 n$ .

Będzie miał $n$ ścian bocznych i dwie ściany, które są podstawami, czyli $S = n + 2$ .

Zauważmy, że $W + K - S = 2 n + n + 2 - 3 n = 2$ .

Wniosek:

Każdy graniastosłup spełnia wzór Eulera.

Słownik

wielościan

bryła, której wszystkie ściany są wielokątami spełniającymi warunki: każde dwie ściany mają wspólną krawędź, wierzchołek lub nie mają części wspólnej, każda krawędź jest wspólna dla dokładnie dwóch ścian, każdy wierzchołek jest wspólny dla co najmniej trzech krawędzi

wielościan wypukły

wielościan, który w całości znajduje się po jednej stronie każdej płaszczyzny wyznaczonej przez jedną z jego ścian

Wprowadzenie

Animacja 3D

Wielościan wypukły

Liczba wierzchołków, krawędzi i ścian w wielościanach

Twierdzenie Eulera

Twierdzenie Eulera, a graniastosłupy

Słownik