Przeczytaj

Zacznijmy od przeanalizowania poniższego rysunku.

R1Ph6YHlWE7Dx

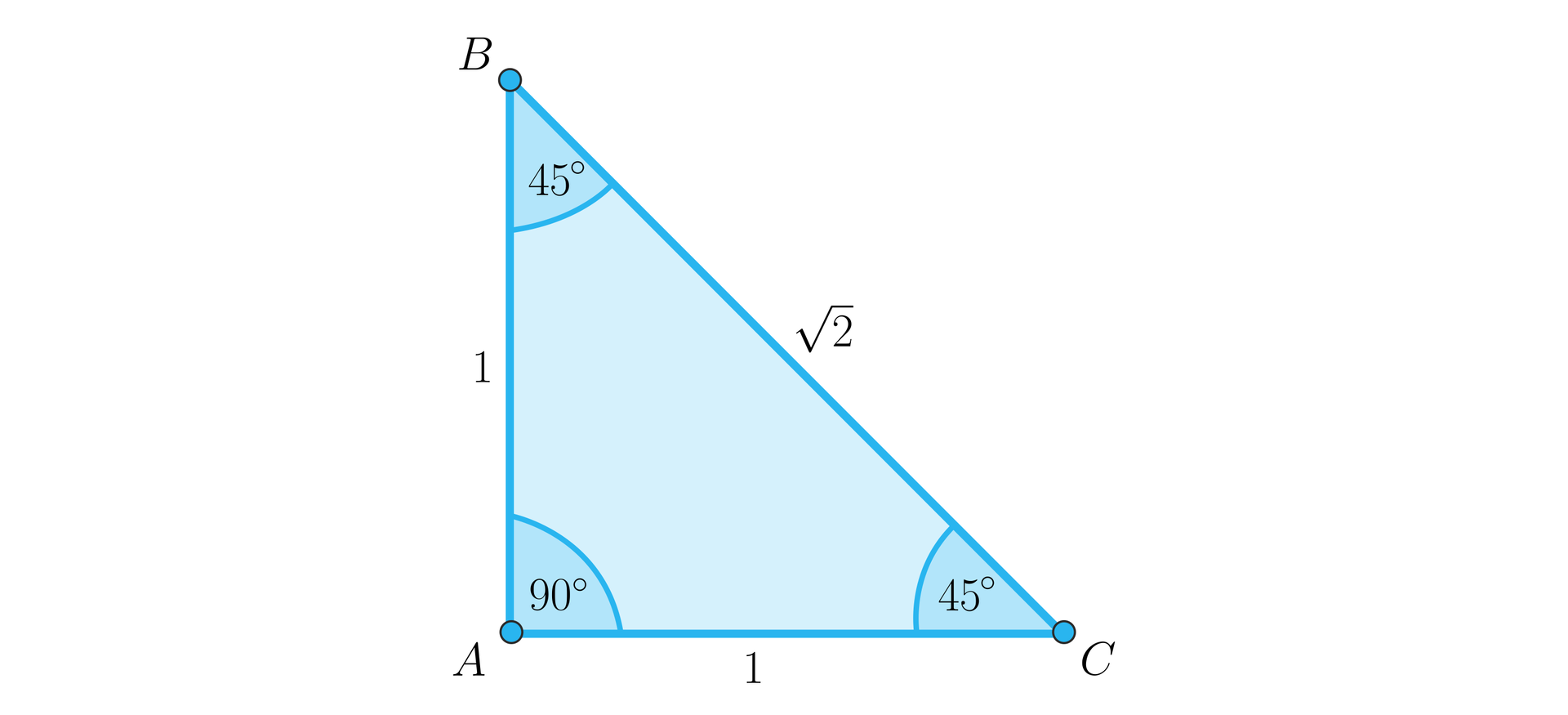
Ilustracja przedstawia trójkąt prostokątny równoramienny ABC. Przy wierzchołku A oznaczono kąt 90 stopni, przy wierzchołkach B i C oznaczono kąty 45 stopni. Bok AC będący podstawą ma długość 1, pionowy bok AB ma również długość 1, a przekątna BC ma długość pierwiastek kwadratowy z dwóch.

Przedstawiony został równoramienny i prostokątny trójkąt $A B C$ . Ramiona w takim trójkącie stanowią jednocześnie jego przyprostokątne i są równej długości. Ponadto, kąty $∢ A B C$ i $∢ B C A$ są sobie równe i wynoszą $45 °$ . Obliczymy wartości wszystkich funkcji trygonometrycznych dla kąta $∢ A B C$ .

Aby policzyć sinus kąta $∢ A B C$ , dzielimy długość przyprostokątnej leżącej naprzeciw badanego kąta przez długość przeciwprostokątnej:

\sin 45 ° = \frac{|A C|}{|B C|} = \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}

Aby obliczyć cosinus kąta $∢ A B C$ , obliczamy stosunek długości przyprostokątnej leżącej przy badanym kącie i przeciwprostokątnej:

\cos 45 ° = \frac{|A B|}{|B C|} = \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}

W celu znalezienia wartości tangensa kąta $∢ A B C$ , dzielimy długość przyprostokątnej leżącej naprzeciwko badanego kąta przez długość odcinka stanowiącego przyprostokątną leżącą przy badanym kącie:

tg 45 ° = \frac{|A C|}{|A B|} = \frac{1}{1} = 1

O wartościach funkcji trygonometrycznych dla kąta

45 °

Twierdzenie: O wartościach funkcji trygonometrycznych dla kąta

45 °

Funkcje trygonometrycznefunkcje trygonometryczneFunkcje trygonometryczne dla kąta $45 °$ przyjmują następujące wartości:

$\sin 45 ° = \frac{\sqrt{2}}{2}$ ;
$\cos 45 ° = \frac{\sqrt{2}}{2}$ ;
$tg 45 ° = 1$ .

Umiemy już obliczać wartości funkcji trygonometrycznych kąta $45 °$ .

Nasuwającym się teraz pytaniem jest: Jak możemy tę wiedzę wykorzystać?

Znajomość powyższych wartości znajduje swoje zastosowania w sytuacjach, które wymagają wyznaczenia długości boków trójkąta równoramiennego prostokątnego, a dysponujemy długością tylko jednego boku. Możemy wykorzystać tę wiedzę także w innych figurach niż trójkąty. W niektórych sytuacjach jesteśmy w stanie wyodrębnić trójkąt równoramienny prostokątny, dzieląc bardziej złożoną figurę na prostsze składowe.

Prostym przykładem takiej figury może być trapez o pewnych szczególnych własnościach. Gdy ramię trapezu tworzy z podstawą kąt ostry $45 °$ , owo ramię, wysokość trapezu i fragment podstawy tworzą pożądany przez nas trójkąt. Rozważymy teraz sytuację, gdy możemy policzyć pole trapezu mając dane zaledwie dwa boki.

Przykład 1

Obliczymy pole trapezu równoramiennego $A B C D$ przedstawionego na poniższym rysunku.

R1GLmFaJYjQX1

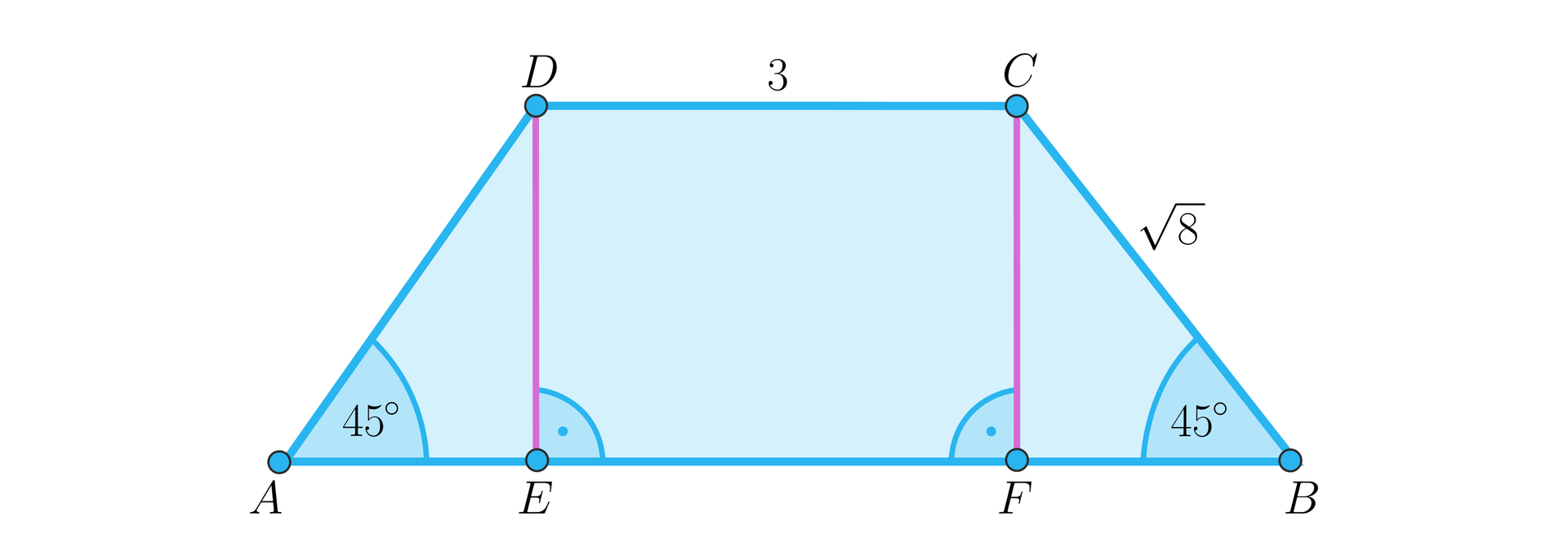
Ilustracja przedstawia trapez równoramienny ABCD. Przy dolnych wierzchołkach A i B oznaczono kąty 45 stopni. Ramiona BC i AD mają długość pierwiastek kwadratowy z ośmiu każde. Górna podstawa CD ma długość trzy. Z wierzchołków C i D upuszczono wysokości: odpowiednio z wierzchołka C upuszczono wysokość do punktu F leżącego na dolnej podstawie, a z wierzchołka D upuszczono wysokość do punktu E leżącego na dolnej podstawie. Przy punktach E i F oznaczono kąty proste między wysokościami a dolną podstawą.

Zauważmy, że punkty $F B C$ tworzą trójkąt równoramienny prostokątny, gdzie odcinek $C F$ jest wysokością trapezu.

Znamy długość przeciwprostokątnej, zatem korzystając z wartości sinusa $45 °$ możemy znaleźć wysokość.

Oznaczając długość odcinka $C F$ przez $h$ mamy:

$\sin 45 ° = \frac{h}{\sqrt{8}}$

$\frac{\sqrt{2}}{2} = \frac{h}{2 \sqrt{2}}$

Mnożąc stronami równość przez $2 \sqrt{2}$ otrzymujemy wartość $h$ :

$h = \frac{2 \cdot \sqrt{2} \cdot \sqrt{2}}{2} = \frac{4}{2} = 2$

Zatem wysokość trapezu $A B C D$ wynosi $h = 2$ .

Aby obliczyć żądane pole powierzchni, brakuje nam jeszcze informacji o długości dolnej podstawy.

Możemy zauważyć, że odcinek $|F B| = |C F| = 2$ .

Ponadto odcinek $|A D| = \sqrt{8}$ , gdyż trapez $A B C D$ jest równoramienny.

W identyczny sposób jak dla trójkąta $F B C$ , możemy policzyć długości boków trójkąta $A E D$ .

Stąd otrzymamy, że odcinek $A E$ ma również długość $|A E| = 2$ .

Długość odcinka $E F$ też jest nam znana, albowiem $|E F| = |C D| = 3$ .

Wynika to z faktu, że $E F C D$ jest prostokątem.

Zatem długość dolnej podstawy wynosi $|A B| = 2 + 3 + 2 = 7$ .

Korzystając ze wzoru na pole trapezu, uzyskujemy końcowy wynik

$P = \frac{(3 + 7) \cdot 2}{2} = 10$ .

W bardziej złożonych zadaniach pojawia się konieczność rozbicia trójkąta na mniejsze trójkąty prostokątne, w których znajomość funkcji trygonometrycznych pozwoli nam wyznaczyć niezbędne długości odcinków.

Przykład 2

W trójkącie prostokątnym równoramiennym $A B C$ długość przeciwprostokątnej wynosi $c = 9 \sqrt{6}$ . Środkowe tego trójkątaśrodkowa trójkątaŚrodkowe tego trójkąta przecinają się w punkcie $D$ , z którego poprowadzono odcinki padające pod kątem prostym na przyprostokątne. Oblicz pole utworzonego w ten sposób kwadratu (na rysunku jest to kwadrat $B E D F$ ).

RRgKyRVJZ7Xjj

Ilustracja przedstawia trójkąt prostokątny równoramienny ABC. Kąt prosty znajduje się przy wierzchołku B, jednak nie jest oznaczony. Z punktu A poprowadzono środkową do boku BC. Z wierzchołka B poprowadzono środkową do punktu G leżącego na przeciwprostokątnej AC. Ta środkowa jest jednocześnie wysokością. Między tą środkową (będącą odcinkiem BG) a przeciwprostokątną AC oznaczono kąt prosty. Z wierzchołka C także poprowadzono środkową do boku AB. Wszystkie środkowe przecinają się w punkcie D. Z punktu D poprowadzono dwa odcinki. Odcinek pionowy DE upuszczony na podstawę BC trójkąta. Między odcinkiem DE i bokiem BC oznaczono kąt prosty. Drugi odcinek poprowadzony z punktu D to odcinek poziomy DF upuszczony na pionowy bok AB trójkąta. Między odcinkiem DF i bokiem AB oznaczono kąt prosty. Na rysunku opisano także długość boku AC - wynosi ona 9 pierwiastków kwadratowych z sześciu.

Zauważmy, że w przypadku trójkąta prostokątnego równoramiennego wysokość poprowadzona z kąta prostego pokrywa się ze środkową trójkąta.

W związku z tym wysokość $h$ poprowadzona z wierzchołka kąta prostego dzieli ten trójkąt na dwa trójkąty o kątach $45 °$ , $45 °$ , $90 °$ .

Otrzymane w ten sposób trójkąty $A B G$ i $B C G$ są przystające, zaś krótszy bok każdego z nich ma długość równą połowie długości przeciwprostokątnej trójkąta $A B C$ , tj.

$h = \frac{9 \sqrt{6}}{2}$ .

Następnie przypomnijmy, że punkt przecięcia środkowych w każdym trójkącie dzieli te środkowe w stosunku $2 : 1$ , gdzie krótszy odcinek łączy środek ciężkości ze środkiem boku.

Punkt przecięcia środkowych w trójkącie nazywany jest zwykle środkiem ciężkości trójkątaśrodek ciężkości trójkątaśrodkiem ciężkości trójkąta.

Zatem punkt $D$ dzieli wysokość $B G$ na dwa odcinki o długościach:

$|D G| = \frac{3}{2} \sqrt{6}$ i $|B D| = \frac{6}{2} \sqrt{6} = 3 \sqrt{6}$

Sytuację tę obrazuje poniższy rysunek (dla czytelności nie zaznaczono na nim środkowych wychodzących z wierzchołków $A$ i $C$ ).

RZoncZpwLwMs6

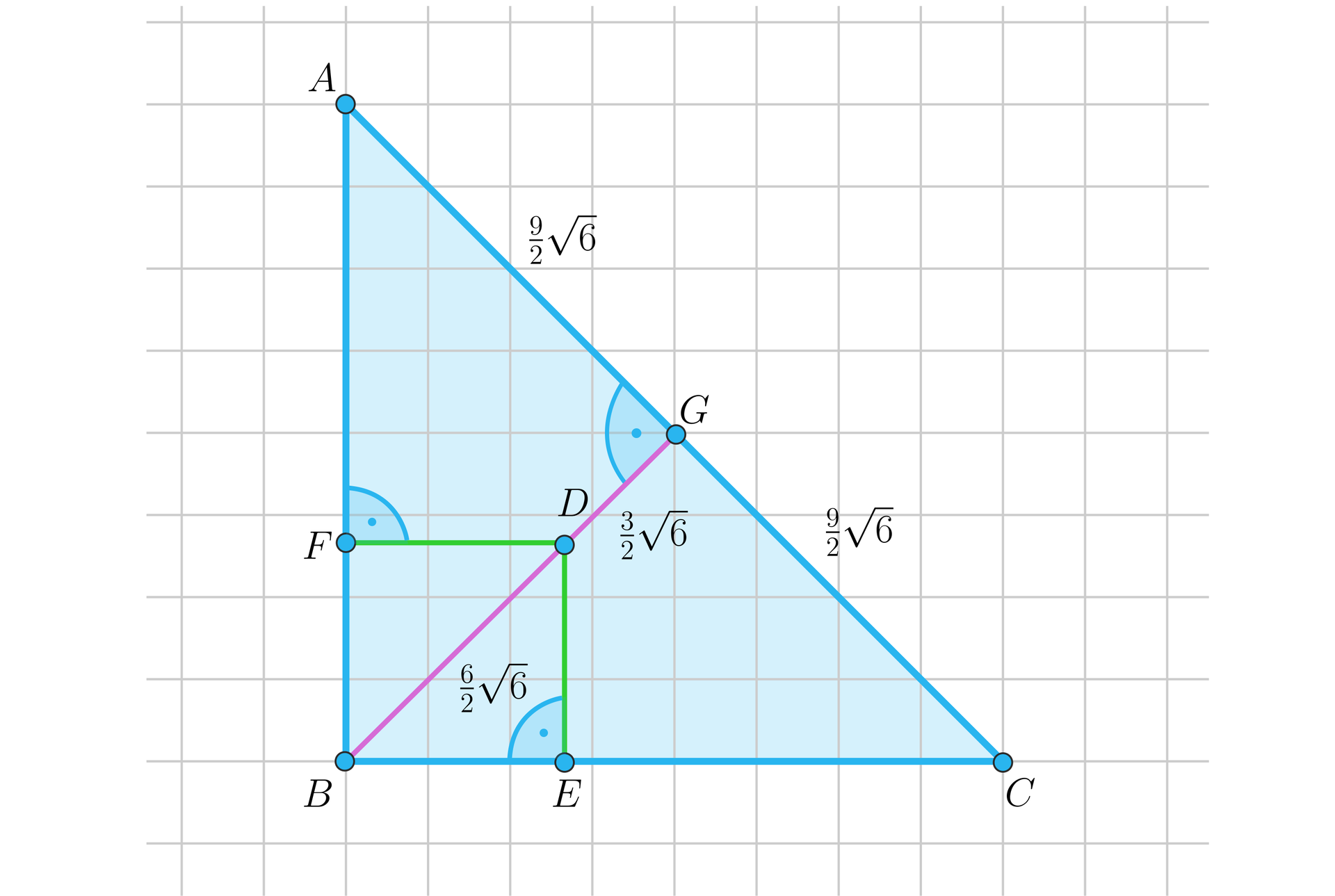
Znamy więc długość odcinka $B D$ , wiemy też, że kąty $∢ B E D$ i $∢ B F D$ są proste (wynika to z treści zadania).

Ponadto, kąty $∢ G B C$ i $∢ A B G$ mają po $45 °$ .

Wykorzystamy funkcję sinus.

$\sin 45 ° = \frac{|D E|}{|B D|}$

$\frac{\sqrt{2}}{2} = \frac{|D E|}{3 \sqrt{6}}$

$\frac{\sqrt{2} \cdot 3 \sqrt{6}}{2} = |D E|$

$|D E| = \frac{3 \sqrt{12}}{2} = \frac{6 \sqrt{3}}{2} = 3 \sqrt{3}$

Znamy więc długość boku kwadratu $B E D F$ . Jego pole wynosi zatem

$P = {(3 \sqrt{3})}^{2} = 9 \cdot 3 = 27$ .

Czasami w zadaniu musimy skorzystać z funkcji trygonometrycznych kąta $45 °$ wielokrotnie by osiągnąć zamierzony cel. Dobrze ilustruje to następujący przykład.

Przykład 3

Bardzo prosty szkic muszli amonitu uzyskano poprzez narysowanie trójkąta prostokątnego równoramiennego $A B C$ , a następnie narysowaniu czterech trójkątów do niego podobnych. Każdy kolejny trójkąt dorysowywano w taki sposób, że przeciwprostokątna poprzedniego trójkąta stawała się przyprostokątną dla kolejnego z nich. Otrzymany rysunek widoczny jest poniżej.

RfPlqDwD4rbqz

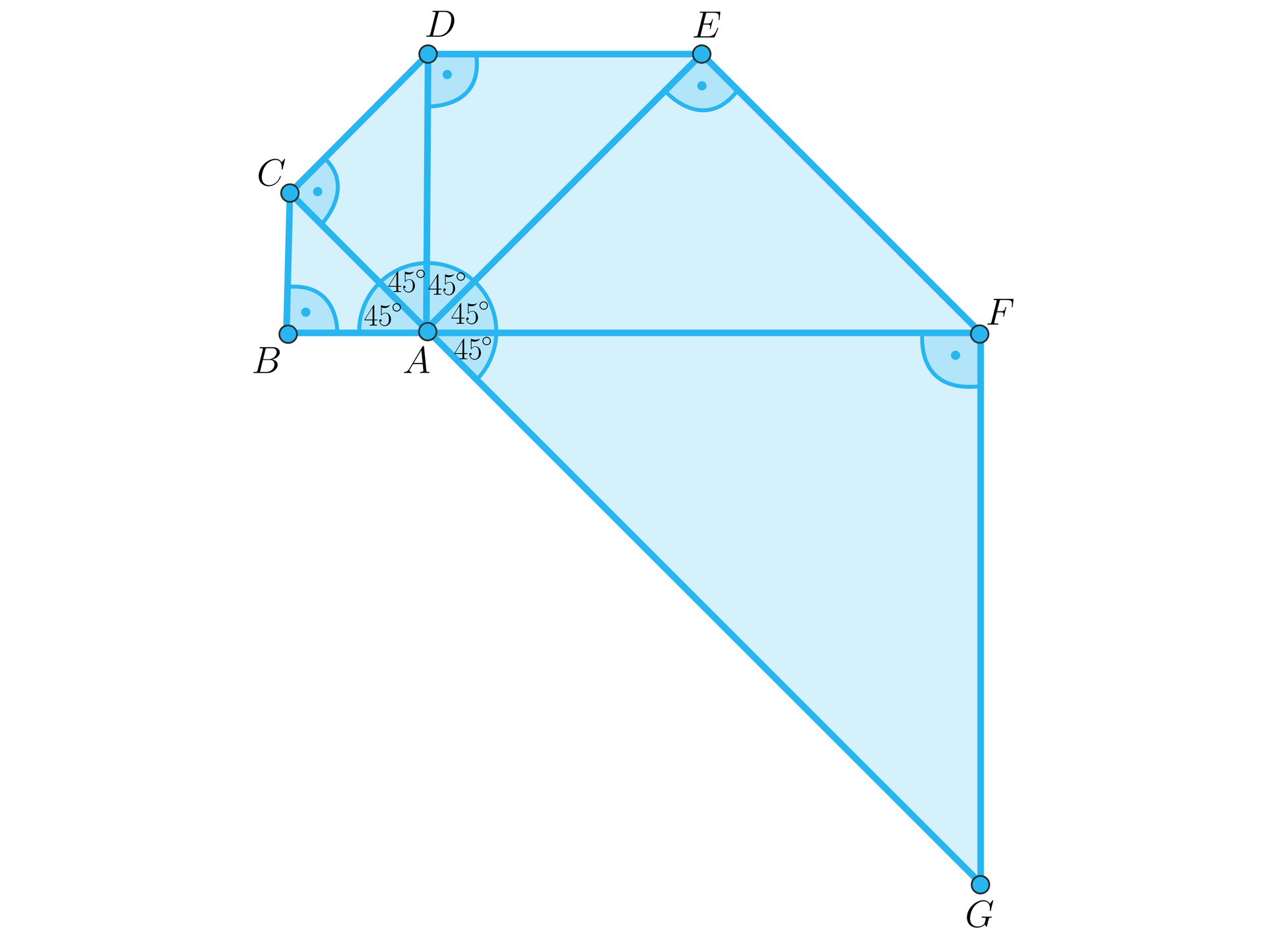
Ilustracja przedstawia pięć trójkątów prostokątnych równoramiennych o wspólnym wierzchołku A i pewnych wspólnych bokach. Trójkąty są coraz większe i każdy kolejny trójkąt oparty jest na przeciwprostokątnej poprzedniego, mniejszego trójkąta. Łącznie figury układają się w spiralę. Pierwszy, najmniejszy trójkąt to trójkąt ABC, gdzie przy wierzchołku B oznaczono kąt prosty, a przy wierzchołku A kąt 45 stopni. Kolejny, większy trójkąt, to trójkąt ACD, gdzie przy wierzchołku C oznaczono kąt prosty, przy A kąt 45 stopni. Na przeciwprostokątnej AD oparto kolejny, większy trójkąt ADE. Przy wierzchołku D oznaczono kąt prosty, przy A 45 stopni. Na przeciwprostokątnej AE oparto kolejny, większy trójkąt AEF. Przy wierzchołku E oznaczono kąt prosty, przy A 45 stopni. Na przeciwprostokątnej AF oparto kolejny, większy trójkąt AFG. Przy wierzchołku G oznaczono kąt prosty, przy A 45 stopni.

Pole tego szkicu wynosi $P = 217 {cm}^{2}$ . Jaką długość ma odcinek $A B$ ? Oblicz obwód tego wielokąta.

Dla ułatwienia oznaczmy długość odcinka $A B$ przez $a$ .

Wówczas pole powierzchni trójkąta $A B C$ wynosi $P_{A B C} = \frac{a^{2}}{2}$ , zaś

$|C D| = |A C| = \frac{a}{\sin 45 °} = \frac{a}{\frac{\sqrt{2}}{2}} = a \sqrt{2}$ .

Zauważmy, że korzystając z tej samej wartości funkcji sinus jesteśmy w stanie wyznaczyć długości wszystkich pozostałych odcinków na tym rysunku:

$|D E| = |A D| = |A C| \cdot \sqrt{2} = 2 a$ ;
$|E F| = |A E| = |A D| \cdot \sqrt{2} = 2 \sqrt{2} a$ ;
$|A F| = |F G| = |A E| \cdot \sqrt{2} = 4 a$ ;
$|A G| = |A F| \cdot \sqrt{2} = 4 \sqrt{2} a$ .

Rozważany przez nas wielokąt jest podzielony na trójkąty, których pola w łatwy sposób jesteśmy w stanie obliczyć.

Mamy bowiem:

$P_{A C D} = \frac{|C D| \cdot |A C|}{2} = \frac{2 a^{2}}{2} = a^{2}$ ;
$P_{A D E} = \frac{|D E| \cdot |A D|}{2} = \frac{2 \cdot 2 a^{2}}{2} = 2 a^{2}$ ;
$P_{A E F} = \frac{|E F| \cdot |A E|}{2} = 4 a^{2}$ ;
$P_{A F G} = \frac{|F G| \cdot |A F|}{2} = 8 a^{2}$ .

Łączne pole powierzchni całego rozważanego wielokąta wynosi zatem:

$P = P_{A B C} + P_{A C D} + P_{A D E} + P_{A E F} + P_{A F G} = 15 \frac{1}{2} a^{2}$ .

Podstawiając znaną nam wartość $P$ otrzymujemy proste równanie kwadratowe, z którego jesteśmy w stanie wyliczyć długość boku $A B$ .

$217 {cm}^{2} = \frac{31 a^{2}}{2}$ ,

$\frac{434}{31} {cm}^{2} = a^{2}$ ,

$a^{2} = 14 {cm}^{2}$ ,

$a = \sqrt{14} cm \lor a = - \sqrt{14} cm$ .

Oczywiście długość boku trójkąta nie może być liczbą ujemną, więc

$|A B| = \sqrt{14} cm$ .

Obwód rozważanego wielokąta otrzymamy sumując odpowiednie długości boków rozpatrywanych w zadaniu trójkątów.

Mamy zatem

$l = |A B| + |B C| + |C D| + |D E| + |E F| + |F G| + |A G| =$

$= a + a + a \sqrt{2} + 2 a + 2 \sqrt{2} a + 4 a + 4 \sqrt{2} a =$

$= 8 a + 7 \sqrt{2} a = (8 \sqrt{14} + 7 \sqrt{28}) cm$ .

Ostatecznie obwód tego wielokąta wynosi $8 \sqrt{14} + 14 \sqrt{7} cm$ , zaś długość boku $A B$ to $\sqrt{14} cm$ .

Słownik

funkcje trygonometryczne

funkcje wyrażające między innymi stosunki między długościami boków trójkąta prostokątnego względem miar jego kątów wewnętrznych; podstawowymi funkcjami trygonometrycznymi są sinus, cosinus, tangens i cotangens

środkowa trójkąta

odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku; każdy trójkąt ma trzy środkowe, odpowiadające poszczególnym jego wierzchołkom

środek ciężkości trójkąta

punkt, w którym przecinają się wszystkie trzy środkowe trójkąta (inną jego nazwą jest barycentrum); punkt ten dzieli każdą ze środkowych na dwie części, przy czym odcinek łączący barycentrum z wierzchołkiem jest dwukrotnie dłuższy od odcinka łączącego środek ciężkości trójkąta ze środkiem boku

Wprowadzenie

Galeria zdjęć interaktywnych

Słownik