Rozstrzygniemy, czy proste o podanych równaniach są równoległe.

a) $k$ : $y=\sqrt{3}x-x+1$, $l$ : $y=x-\sqrt{3}x+5$

Wyznaczmy najpierw współczynniki kierunkowe podanych prostych:

$k$ : $y=\sqrt{3}x-x+1=\left(\sqrt{3}-1\right)x+1 \Rightarrow a_1=\sqrt{3}-1$,

$l$ : $y=x-\sqrt{3}x+5=\left(1-\sqrt{3}\right)x+5\Rightarrow a_2=1-\sqrt{3}=-\left(\sqrt{3}-1\right)$

Zauważmy, że wyznaczone współczynniki kierunkowe są liczbami przeciwnymi. Zatem proste nie są równoległe.

b) $k$ : $y=\sqrt{2}x-x+4$, $l$ : $y=\frac{x}{\left(\sqrt{2}+1\right)}-7$

Wyznaczmy najpierw współczynniki kierunkowe podanych prostych:

$k$ : $y=\sqrt{2}x-x+4=\left(\sqrt{2}-1\right)x+4\Rightarrow a_1=\sqrt{2}-1$

$l$ : $y=\frac{x}{\left(2+1\right)}-7\Rightarrow a_2=\frac{1}{\left(\sqrt{2}+1\right)}=\frac{1}{\left(\sqrt{2}+1\right)}· \frac{\left(\sqrt{2}-1\right)}{\left(\sqrt{2}-1\right)}=\left(\sqrt{2}-1\right)·\left(2-1\right)=$

$=\sqrt{2}-1$

Zauważmy, że wyznaczone współczynniki kierunkowe są równe. Zatem proste są równoległe.

Wyznaczymy równanie kierunkowe prostejrównanie kierunkowe prostejrównanie kierunkowe prostej przechodzącej przez punkt $A$ o współrzędnych $\left(-0,5;4\right)$ równoległej do prostej o równaniu $y=\left(-2x\right)+5$.

Prosta taka ma równanie postaci $y=ax+b$.

Ponieważ ma być ona równoległa do prostej o równaniu $y=\left(-2x\right)+5$, więc $a=\left(-2\right)$.

Aby wyznaczyć współczynnik $b$ wystarczy do równania $y=\left(-2x\right)+b$ podstawić współrzędne punktu $A$:

$4=\left(-2\right)·\left(-0,5\right)+b$

$4=1+b$

$b=3$

Zatem szukane równanie prostej to $y=\left(-2x\right)+3$.

Wyznaczymy wartość parametru $m$, dla którego proste o równaniach $y=x-mx+m$ i $y=2mx-5x-9$ są równoległe.

Zaczniemy od uporządkowania równań, aby odczytać współczynniki kierunkowe:

$y=x-mx+m=\left(1-m\right)x+m\Rightarrow a_1=1-m$

$y=2mx-5x-9=\left(2m-5\right)x-9\Rightarrow a_2=2m-5$

Ponieważ proste są równoległe dokładnie wtedy, gdy mają równe współczynniki kierunkowe, wystarczy więc rozwiązać równanie:

$1-m=2m-5$

$-3m=\left(-6\right)$

$m=2$

Wobec powyższego jedyna wartość parametru $m$, dla której proste o równaniach $y=x-mx+m$ i $y=2mx-5x-9$ są równoległe wynosi $2$.

Dwa boki równoległoboku $ABCD$ zawarte są w prostych o równaniach $y=2x-1$ oraz $y=\left(-x\right)-1$. Ponadto $A=\left(3;5\right)$ i $C=\left(4;-5\right)$. Wyznacz równania prostych zawierających pozostałe dwa boki równoległoboku oraz współrzędne wierzchołków $B$ i $D$.

RvrvnbgHCHE5Z

Ilustracja przedstawia układ współrzędnych. Oś pozioma X ma liczby z zakresu od -1 do osiem. Oś pionowa Y ma liczby z zakresu od -5 do pięć. Zaznaczono cztery punkty A B C oraz D, podane zostały tylko współrzędne: $A=\left(3;5\right)$ oraz $C=\left(4;-5\right)$. Narysowano prostą $y=2x-1$, przechodzi ona przez punkty B oraz A. Narysowano kolejną prostą $y=-x-1$, przechodzi ona przez punkty B oraz C. Punkt B to punkt przecięcia tych dwóch prostych. Narysowano prostą równoległą do prostej $y=2x-1$, nie znamy jej równania. Prosta ta przechodzi przez punkty C oraz D. Narysowano prostą równoległą do prostej $y=-x-1$, nie znamy jej równania. Przechodzi przez punkty A oraz D. Punkt D to punkt przecięcia dwóch nieznanych prostych. Wszystkie narysowane proste tworzą równoległobok A B C D.

Współrzędne trzeciego wierzchołka równoległoboku - nazwijmy go $B$ - możemy obliczyć rozwiązując układ równań opisujących obie proste. W tym szczególnym przypadku możemy zauważyć, że obie proste przecinają oś $Y$ w punkcie $\left(0;-1\right)$ i nie są to te same proste, zatem jest to ich jedyny punkt wspólny. Stąd $B=\left(0;-1\right)$.

Zauważmy, że punkt $A=\left(3;5\right)$ należy do prostej o równaniu $y=2x-1$, ponieważ współrzędne punktu $A$ spełniają równanie tej prostej. Ponadto punkt $C$ leży na prostej o równaniu $y=\left(-x\right)-1$.

Wyznaczymy teraz równanie prostej $AD$.

Ponieważ jest ona równoległa do prostej $BC$ (więc równania obu prostych mają równe współczynniki kierunkowe), to jej równanie ma postać $y=\left(-x\right)+b$. Wyraz wolny $b$ możemy wyznaczyć, korzystając z faktu, że punkt $A=\left(3;5\right)$ należy do tej prostej. Po podstawieniu współrzędnych punktu $A=\left(3;5\right)$ do równania $y=\left(-x\right)+b$ otrzymamy:

$5=\left(-3\right)+b$

$b=8$

Zatem równanie prostej $AD$ to $y=\left(-x\right)+8$.

Analogicznie postąpimy w przypadku prostej $CD$. Ponieważ prosta $CD$ jest równoległa do prostej $AB$, zatem jej równanie ma taki sam współczynnik kierunkowy jak równanie prostej $AB$. 

Równanie kierunkowe prostejrównanie kierunkowe prostejRównanie kierunkowe prostej $CD$ ma postać $y=2x+b_1$. Aby wyznaczyć wyraz wolny $b_1$ podstawimy do równania $y=2x+b_1$ współrzędne punktu $C$:

$\left(-5\right)=2·4+b_1$

$\left(-5\right)-8=b_1$

$\left(-13\right)=b_1$

Zatem równanie prostej $CD$ to $y=2x-13$.

Aby wyznaczyć współrzędne wierzchołka $D$, wystarczy rozwiązać układ równań:

$\left\{\begin{array}{l}y=\left(-x\right)+8\\ y=2x-13\end{array}\right.$

Z powyższego układu równań wynika

$\left(-x\right)+8=2x-13$

$3x=21$

$x=7$

$\left\{\begin{array}{l}x=7\\ y=\left(-7\right)+8=1\end{array}\right.$

Zatem współrzędne wierzchołka $D$ to $\left(7,1\right)$.

Dane są współrzędne trzech punktów $X=\left(2;3\right)$, $Y=\left(4;-1\right)$, $Z=\left(5;0\right)$. Wyznacz współrzędne takich punktów $A$, aby wszystkie cztery punkty $X$, $Y$, $Z$ i $A$ byłby wierzchołkami równoległoboku.

Zauważmy najpierw, że będą trzy takie punkty $A$:

W pierwszej kolejności wyznaczymy równania prostych $XY$, $YZ$ i $XZ$.

Ponieważ żadna z tych prostych nie jest równoległa do osi $Y$, ich równania są postaci $y=ax+b$.

Aby wyznaczyć równanie prostej $XY$, tworząc układ równiań podstawiamy do równania $y=ax+b$ najpierw współrzędne punktu $X$, potem współrzędne punktu $Y$

$\left\{\begin{array}{l}3=2a+b\\ \left(-1\right)=4a+b\end{array}\right.$

Po odjęciu równań stronami otrzymujemy

$4=\left(-2a\right)$

$a=\left(-2\right)$

$\left\{\begin{array}{l}a=\left(-2\right)\\ b=3-2·\left(-2\right)=7\end{array}\right.$

Zatem równanie prostej $XY$ to $y=-2x+7$.

Analogicznie wyznaczamy równania prostej $YZ: y=x-5$ oraz prostej $XZ: y=\left(-x\right)+5$.

W trzecim przypadku współrzędne punktu $A$ wyznaczymy, rozwiązując układ równań opisujących proste $AX$ i $\mathrm{AZ}$. Otrzymamy wówczas równoległobok $XYZA$.

Ponieważ prosta $AX$ jest równoległa do prostej $YZ$, zatem jej równanie jest postaci $y=x+b_1$. Po podstawieniu za zmienne $x$ i $y$ współrzędnych punktu $X\left(2;3\right)$ wyznaczamy $b_1$:

$3=2+b_1$

$b_1=1$

Zatem równanie prostej $AX$ to $y=x+1$.

Analogicznie wyznaczamy równanie prostej $AZ:y=\left(-2x\right)+10$. Rozwiązując układ równań:

$\left\{\begin{array}{l}y=x+1\\ y=\left(-2x\right)+10\end{array}\right.$

otrzymujemy współrzędne punktu $A=\left(3;4\right)$.

Postępując podobnie otrzymujemy: w przypadku drugim równoległobok $YZXA$, gdzie $A=\left(1;2\right)$ oraz w przypadku pierwszym równoległobok $ZXYA$, gdzie $A=\left(7;-4\right)$.

W prostokątnym układzie współrzędnych narysujemy zbiór wszystkich punktów spełniających warunek $x-1<y\le x+2$.

Zauważmy najpierw, że warunek $x-1=y$ spełniają punkty o współrzędnych $\left(x,y\right)$, które leżą na prostej opisanej tym równaniem. Warunek $x-1<y$ opisuje takie punkty, dla których druga współrzędna jest większa od pierwotnej, a zatem punkty leżące “ponad” prostą o równaniu $x-1=y$.

R1IJxhK1CxQEs

Ilustracja przedstawia układ współrzędnych z poziomą osią X od -5 do pięć oraz z pionową osią Y od -5 do pięć. Na płaszczyźnie linią przerywaną narysowano ukośną prostą przebiegającą między innymi przez punkty nawias zero średnik minus jeden zamknięcie nawiasu oraz przez punkt nawias jeden średnik zero zamknięcie nawiasu. Zaznaczono część płaszczyzny nad prostą.

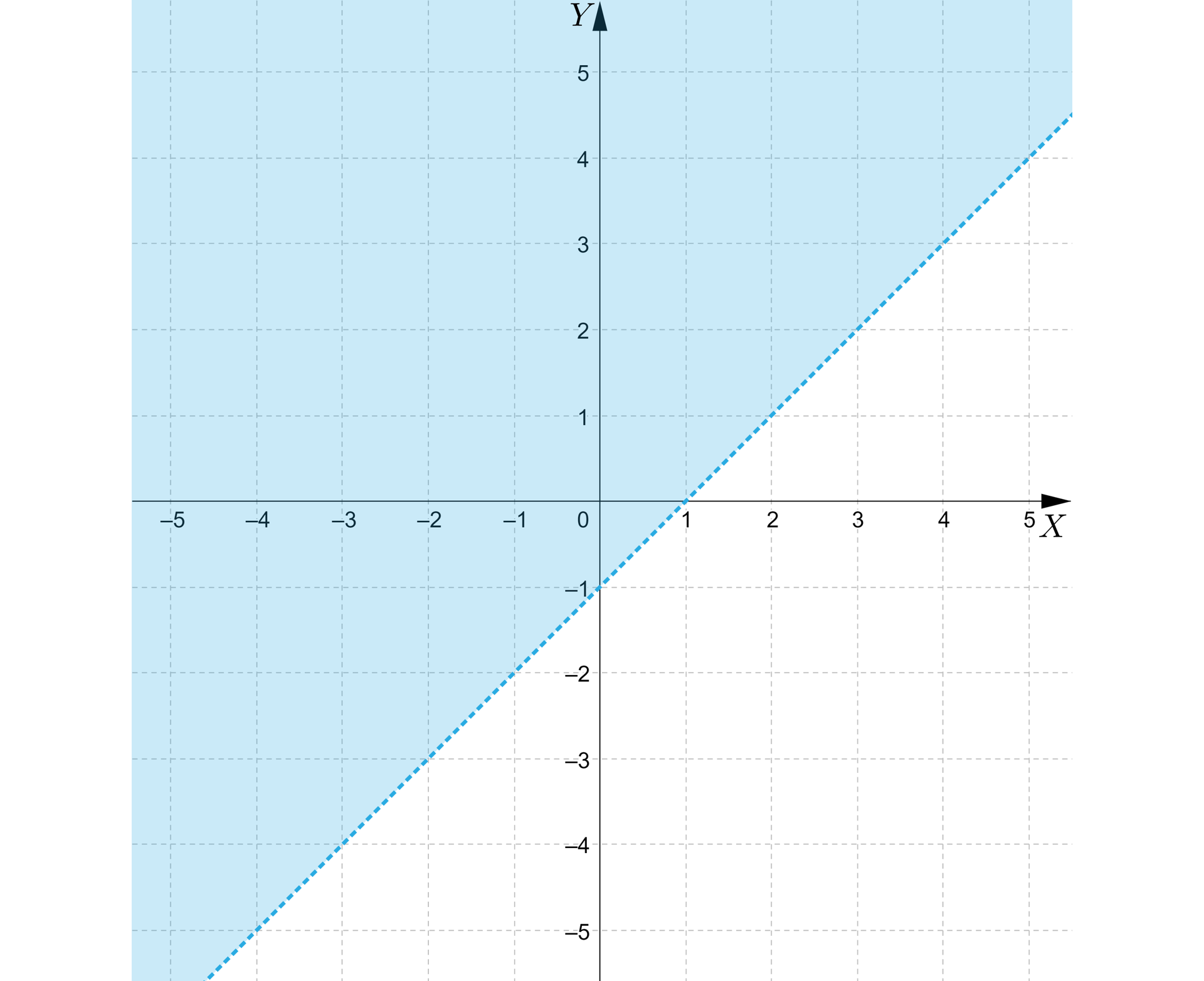
Analogicznie możemy dojść do wniosku, że warunek $y\le x+2$ opisuje punkty, które leżą „na” prostej lub „pod” prostą o równaniu $y=x+2$.

R1JFICZUAyyEk

Ilustracja przedstawia dwuwymiarowy układ współrzędnych z poziomą osią X od -5 do pięć oraz z pionową osią Y od -5 do pięć. Na płaszczyźnie linią ciągłą narysowano ukośną prostą przebiegającą między innymi przez punkty nawias minus dwa średnik zero zamknięcie nawiasu oraz przez punkt nawias zero średnik dwa zamknięcie nawiasu. Zaznaczono kolorem niebieskim część płaszczyzny pod prostą.

Oba warunki jednocześnie spełniają współrzędne punktów, które leżą pomiędzy prostymi o równaniach $x-1=y$ oraz $y=x+2$ lub na prostej o równaniu $y=x+2$.

R11jrsVO0C6ZL

Ilustracja przedstawia układ współrzędnych z osią poziomą X od -5 do 5 i osią pionową Y od -5 do pięć. Na płaszczyźnie narysowano dwie ukośne równoległe proste. Pierwsza prosta leżąca powyżej narysowana jest linią ciągłą i przebiega między innymi przez punkty nawias minus dwa średnik zero zamknięcie nawiasu oraz przez punkt nawias zero średnik dwa zamknięcie nawiasu. Druga prosta narysowana jest linią przerywaną i przebiega między innymi przez punkty nawias minus jeden średnik zero zamknięcie nawiasu oraz przez punkt nawias jeden średnik zero zamknięcie nawiasu. Zaznaczono obszar znajdujący pomiędzy prostymi, jest to ukośny pas.

równanie postaci $y=ax+b$, $a,b\in \mathrm{ℝ}$; można nim opisać każdą prostą, która nie jest równoległa do osi $Y$

twierdzenie matematyczne, które orzeka, że proste opisane równaniami kierunkowymi są równoległe wtedy i tylko wtedy, gdy współczynniki kierunkowe tych prostych są równe