Jak rozpoznawać algorytmy o kwadratowej złożoności czasowej?

Wyobraźmy sobie, że analizujemy pewien algorytm o kwadratowej złożoności czasowej. Niech funkcja $f$ wyznacza dokładną liczbę operacji wykonywanych przez program w zależności od ilości danych wejściowych. Przyjmijmy, że ma ona następującą postać:

przy czym $k$ jest pewną stałą. Jak w takim razie może być zbudowany algorytm? Spróbujmy zapisać funkcję $f$ w nieco inny sposób, a mianowicie:

Przedstawimy kilka propozycji programów, w których zastosowanie znajdą algorytmy o kwadratowej złożoności czasowej.

Obliczanie sumy długości boków i przekątnych figury

Pierwszy program przyjmuje na wejście współrzędne geometryczne punktów$A_1$, $A_2$, $\dots$, $A_n$, będących wierzchołkami figury wypukłejfigura wypukłafigury wypukłej. Na podstawie tych danych wyznaczane są długości wszystkich odcinków $A_iA_j$, przy czym $i=1,\ 2,\ \dots,\ \left(n-1\right)$ oraz $j=\left(i+1\right),\ \left(i+2\right),\ \dots, n$. Otrzymane wartości są następnie sumowane, dzięki czemu otrzymujemy pożądaną sumę długości boków i przekątnych figury.

R1GixojeLFAsQ

Ilustracja przedstawia pięciokąt o wierzchołkach od $A_1$ do $A_5$. Wierzchołki są wyróżnione jako zamalowane punkty i są ze sobą połączone liniami przerywanymi, które tworzą pięcioramienną gwiazdę. Wnętrze wielokąta jest zamalowane.

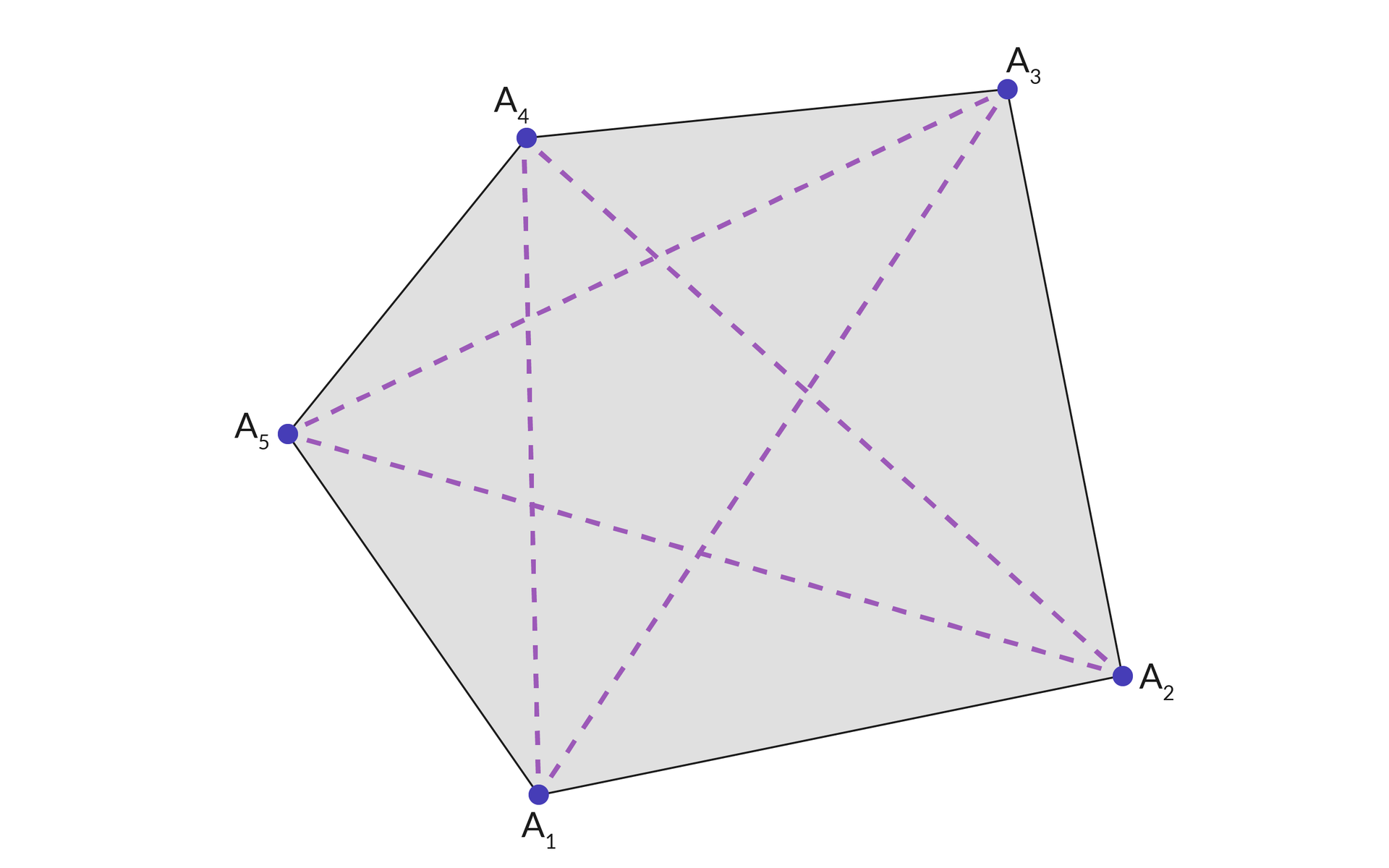
Zapiszmy odpowiedni algorytm w postaci pseudokodu. Niech Punkty oznaczają zbiór n punktów podanych jako dane wejściowe. Dodatkowo niech instrukcja Punkty[i] oznacza odwołanie się do współrzędnych i-tego punktu.

suma ← 0
i ← 1

Dopóki i <= (n - 1) wykonuj
	j ← i + 1
    
	Dopóki j <= n wykonuj
		suma ← suma + odleglosc(Punkty[i], Punkty[j])
		j ← j + 1
        
	i ← i + 1

wypisz(suma)

Dla każdego punktu spośród n podanych na wejściu obliczana jest odległość między nim a pozostałymi punktami. Dodatkowo zadbaliśmy o to, aby odległość między każdą parą różnych punktów była liczona dokładnie raz. Dzięki temu w trakcie rozpatrywania i-tego z kolei punktu, obliczamy odległość dokładnie (n - i) razy. W rezultacie funkcja $f$ opisująca liczbę wykonywanych operacji przybierze następującą postać:

Po skorzystaniu ze wzoru na sumę ciągu arytmetycznego otrzymujemy:

Udowodniliśmy zatem, że nasz algorytm ma kwadratową złożoność czasową.

Rysowanie figur w oknie konsoli

Kolejnym pomysłem na zastosowanie algorytmu o czasowej złożoności kwadratowej jest wypisywanie w oknie konsoli kwadratu zbudowanego ze znaków #. Jego bok składa się z $n$ znaków, przy czym o wartości $n$ decyduje użytkownik na początku działania programu.

RFaS6IpLKTIWI

Ilustracja przedstawia trzy kwadraty składające się z haszy. W lewym górnym rogu znajduje się kwadrat o wymiarze 5 na 5 haszy z nagłówkiem: "podaj n : 5". Poniżej znajduje się kwadrat o wymiarach 10 na 10 haszy z nagłówkiem "podaj n : 10". Po prawej stronie znajduje się kwadrat 20 na 20 haszy z nagłówkiem "podaj n : 20".

Zapiszmy zatem algorytm w postaci pseudokodu.

wczytaj(n)
i ← 1

Dopóki i <= n wykonuj
	j ← 1
    
	Dopóki j <= n wykonuj
		wypisz("#")
		j ← j + 1
        
	wypisz("\n")
	i ← i + 1

Dosyć nietypowa może się wydać instrukcja wypisz("\n"). Symbol \n jest jednym z symboli sterujących. Mówi on funkcji wypisującej znaki, że należy przejść do nowej linii. Rezultat jest taki sam jak po naciśnięciu klawisza [Enter] w czasie pracy z edytorem tekstu.

Udowodnienie, że zastosowany algorytm ma kwadratową złożoność czasową jest proste. Zauważmy, że skoro bok kwadratu składa się z $n$ znaków #, to musimy ich wypisać $n^2$. W konsekwencji należy wykonać około $n^2$ operacji; oznacza to, że mamy do czynienia z kwadratową złożonością czasową.

Sortowanie elementów

R1K8S5r88MxPd1

Ilustracja przedstawia eliptyczny zbiór z zielonym wnętrzem. W zbiorze znajdują się białe koła, a w każdym z nich wpisana jest jedna z następujących liczb: 1 po lewo, 4 w dolnej części, 7 po prawo, 10 w górnej części zbioru.

Ostatnim przykładem jest sortowanie $n$ liczb podanych na wejściu przez użytkownika. Ponieważ w czasie obecnej lekcji nie omawiamy sposobów przechowywania danych, nie będziemy zajmować się tym zagadnieniem. Ograniczymy się do przedstawienia idei algorytmu sortowania.

Spośród $n$ liczb będzie wybierana najmniejsza. Zostanie ona usunięta z przeszukiwanego zbioru i wypisana na wyjściu. Następnie te same operacje będą powtarzane dla zbiorów złożonych z $n-1, n-2,\ \dots$ elementów.

R18gP1EFgkdHx

Ilustracja przedstawia eliptyczny zbiór z zielonym wnętrzem. W zbiorze znajdują się koła, a w każdym z nich wpisana jest jedna z następujących liczb: 1 po lewo, 4 w dolnej części, 7 po prawo, 10 w górnej części zbioru. Koła 4, 7 i 10 są zakolorowane na żółto, a koło 1 jest białe. Po prawej stronie zbioru znajduje się pozioma strzałka skierowana w prawo. Poniżej narysowano podobny eliptyczny zbiór z zielonym wnętrzem. W zbiorze znajdują się koła, a w każdym z nich wpisana jest jedna z następujących liczb: 4 w dolnej części, 7 po prawo, 10 w górnej części zbioru. Koła 7 i 10 są zakolorowane na żółto, a koło 4 jest białe. Po prawej stronie zbioru znajduje się pozioma strzałka skierowana w prawo na koło z liczbą 1 zakolorowane na żółto, które wyjęto ze zbioru. Poniżej narysowano podobny eliptyczny zbiór z zielonym wnętrzem. W zbiorze znajdują się koła, a w każdym z nich wpisana jest jedna z następujących liczb: 7 po prawo, 10 w górnej części zbioru. Koło 10 jest zakolorowane na żółto, a koło 7 jest białe. Po prawej stronie zbioru znajduje się pozioma strzałka skierowana w prawo na koła z liczbami 1 i 4, które są zakolorowane na żółto. Poniżej narysowano podobny eliptyczny zbiór z zielonym wnętrzem. W zbiorze znajduje się białe koło z liczbą 10. Po prawej stronie zbioru znajduje się pozioma strzałka skierowana w prawo na żółte koła z liczbami 1, 4 i 7. Poniżej narysowano podobny eliptyczny zbiór z zielonym wnętrzem. Zbiór jest pusty. Po prawej stronie zbioru znajduje się pozioma strzałka skierowana w prawo na żółte koła z liczbami 1, 4, 7 i 10.

Niżej znajduje się algorytm przedstawiony w postaci pseudokodu. Niech Liczby oznaczają zbiór n liczb podanych na wejściu. Natomiast instrukcja Liczby[i] oznacza odwołanie się do i-tej liczby.

Dopóki n > 0 wykonuj
	minimum ← Punkty[1]
    i ← 2
    
	Dopóki i <= n wykonuj
		Jeżeli minimum > Punkty[i]
			minimum ← Punkty[i]
            
		i ← i + 1
        
	wypisz(minimum)
	usun_ze_zbioru(minimum)
	n ← n - 1

Ile operacji wykona program? Znalezienie najmniejszej wartości w zbiorze $n$-elementowym wymaga wykonania $\left(n-1\right)$ porównań. Stosując omawiany algorytm, będziemy wyszukiwać najmniejszy element kolejno w zbiorze $n$-elementowym, następnie w $\left(n-1\right)$-elementowym i tak dalej. W rezultacie funkcja $f$ opisująca liczbę wykonywanych operacji przybierze następującą postać:

Jest to suma ciągu arytmetycznego o wyrazie początkowym równym $\left(n-1\right)$ i różnicy wynoszącej $-1$. Korzystając z wzoru na sumę takiego ciągu, otrzymujemy:

Udowodniliśmy zatem, że złożoność czasowa przedstawionego algorytmu sortowania jest kwadratowa.

Przybliżony czas realizacji algorytmów o złożoności kwadratowej

Poznaliśmy i nauczyliśmy się rozpoznawać już trzy złożoności czasowe: stałą, liniową i kwadratową. Korzystając z przybliżenia, zgodnie z którym współczesnym komputerom wykonanie miliarda ($10^9$) operacji zajmuje około sekundę, porównajmy czas działania programów bazujących na algorytmach o różnych złożonościach czasowych.

Dla bardzo małej liczby danych wejściowych różnica między algorytmami liniowymi a kwadratowymi jest naprawdę niewielka. Jednak wraz ze wzrostem liczby danych czas działania programu, w którym zaimplementowano algorytm o kwadratowej złożoności czasowej, rośnie w bardzo dużym tempie. Właśnie dlatego tak ważna jest optymalizacja czasowa programów.

Słownik