Przeczytaj
Dwa okręgi leżące na jednej płaszczyźnie, w zależności od odległości między ich środkami i długości ich promieni, mogą nie mieć żadnego punktu wspólnego lub mieć jeden albo dwa punkty wspólne.
Rozważmy dwa okręgi: okrągokrąg o środku i promieniu długości oraz okrąg o środku i promieniu długości .
1. Okręgi nie mają punktów wspólnych, gdy:
a) odległość środków okręgów jest większa od sumy długości ich promieni: . Okręgi te są rozłączne zewnętrznie.
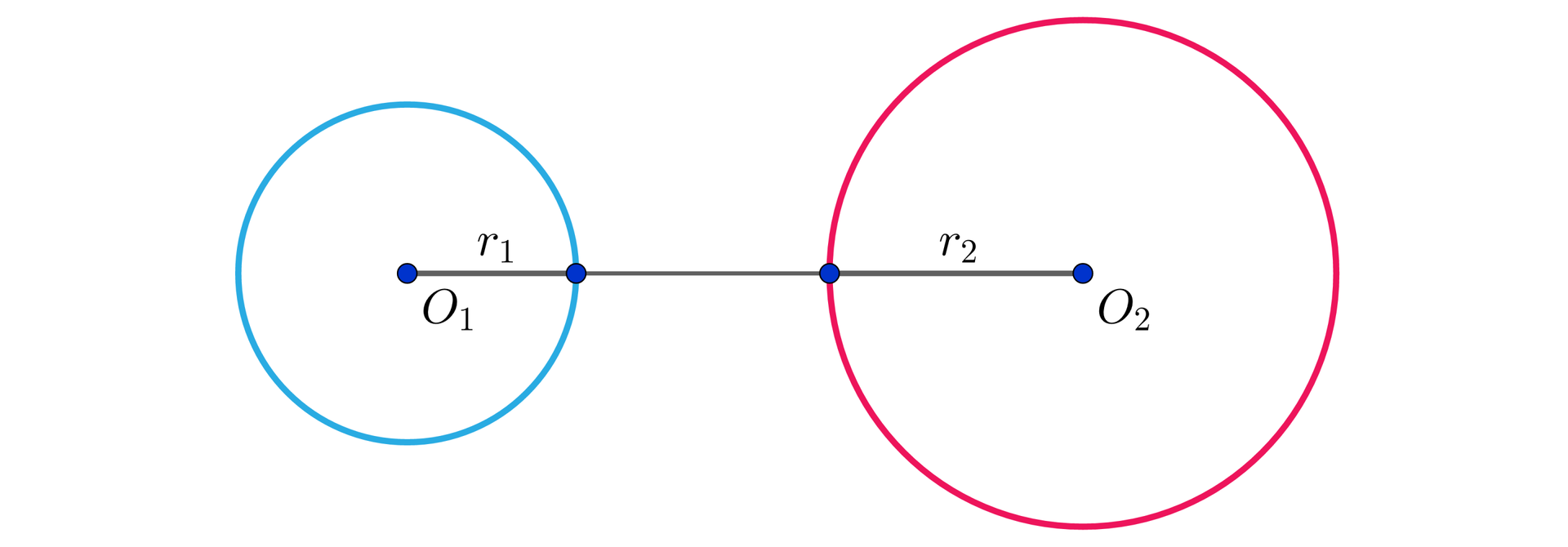
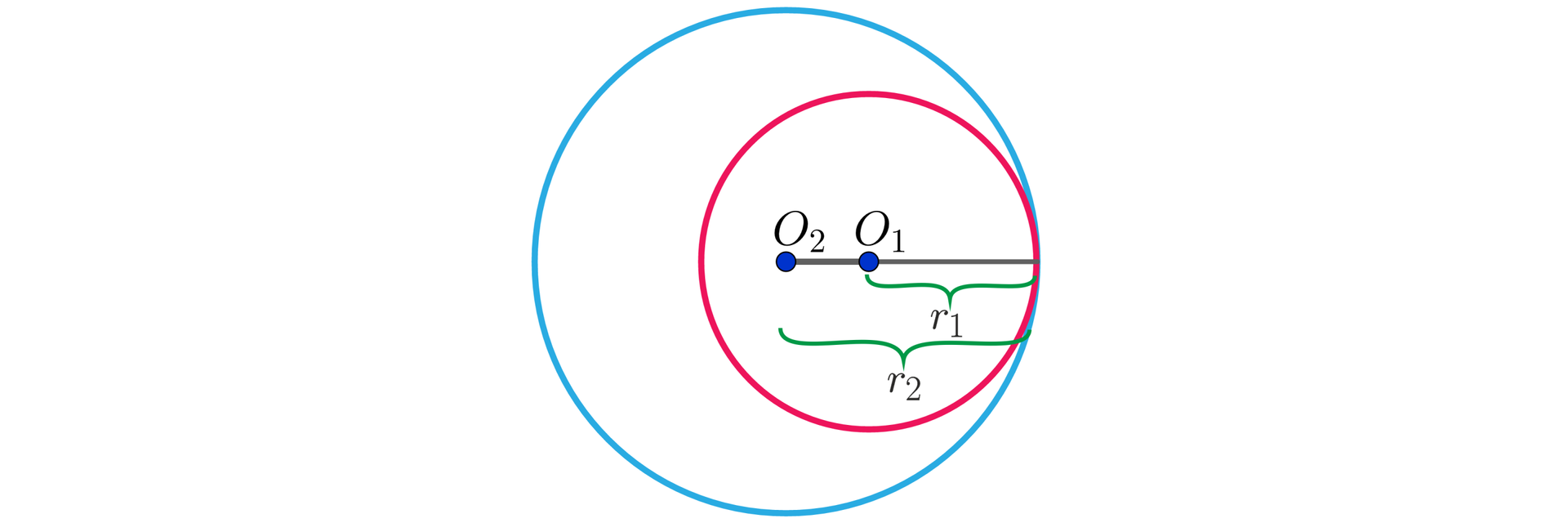
b) odległość środków okręgów jest mniejsza od różnicy długości ich promieni: , . Okręgi te są rozłączne wewnętrznie.
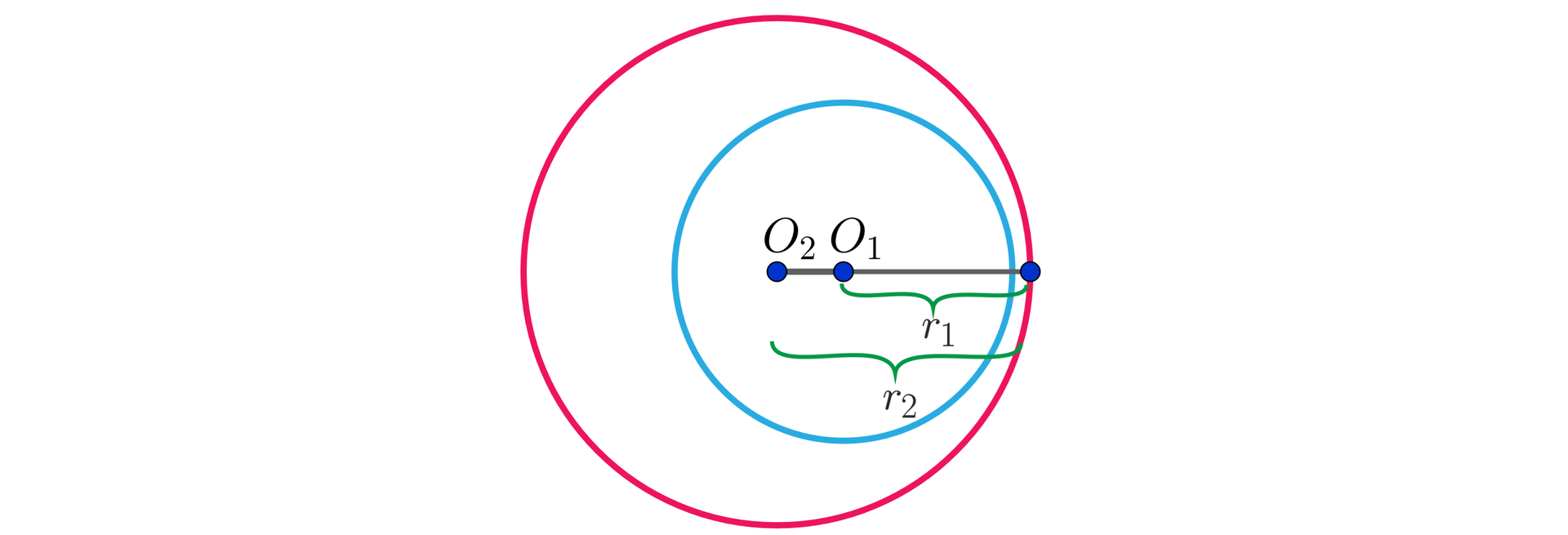
Jeśli , to okręgi nazywamy współśrodkowymi.
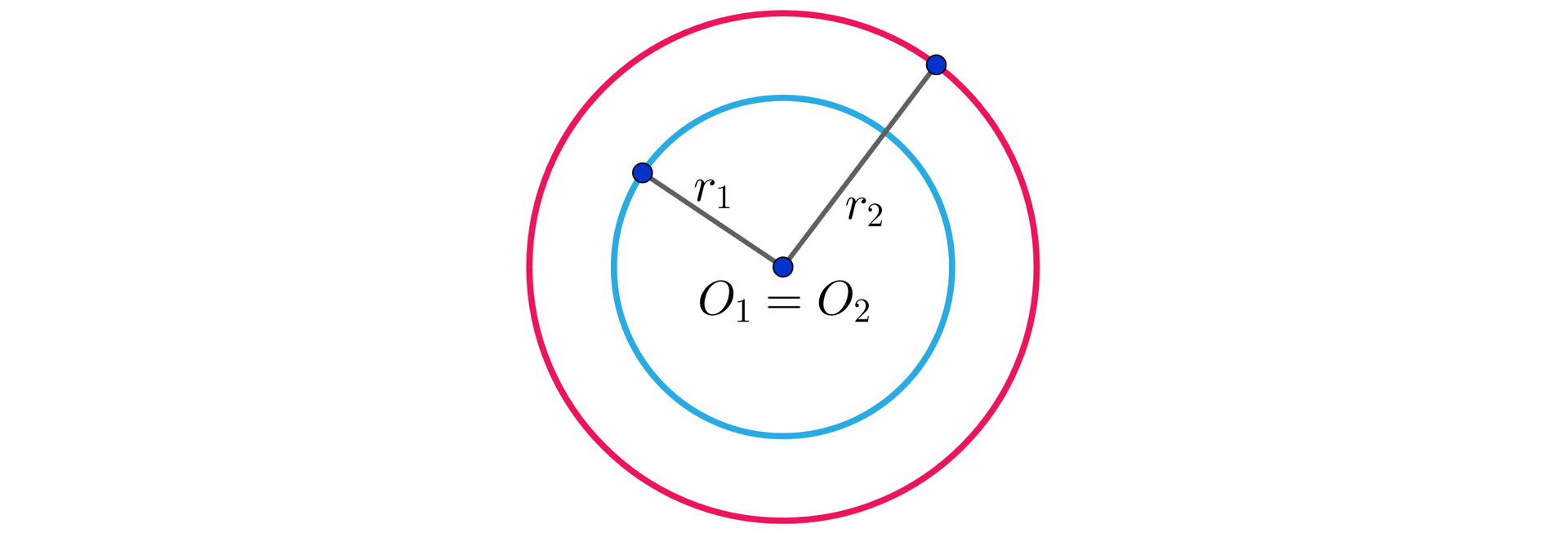
2. Okręgi mają jeden punkt wspólny, gdy:
a) odległość środków okręgów jest równa sumie długości ich promieni: . Okręgi takie nazywamy stycznymi zewnętrznie.
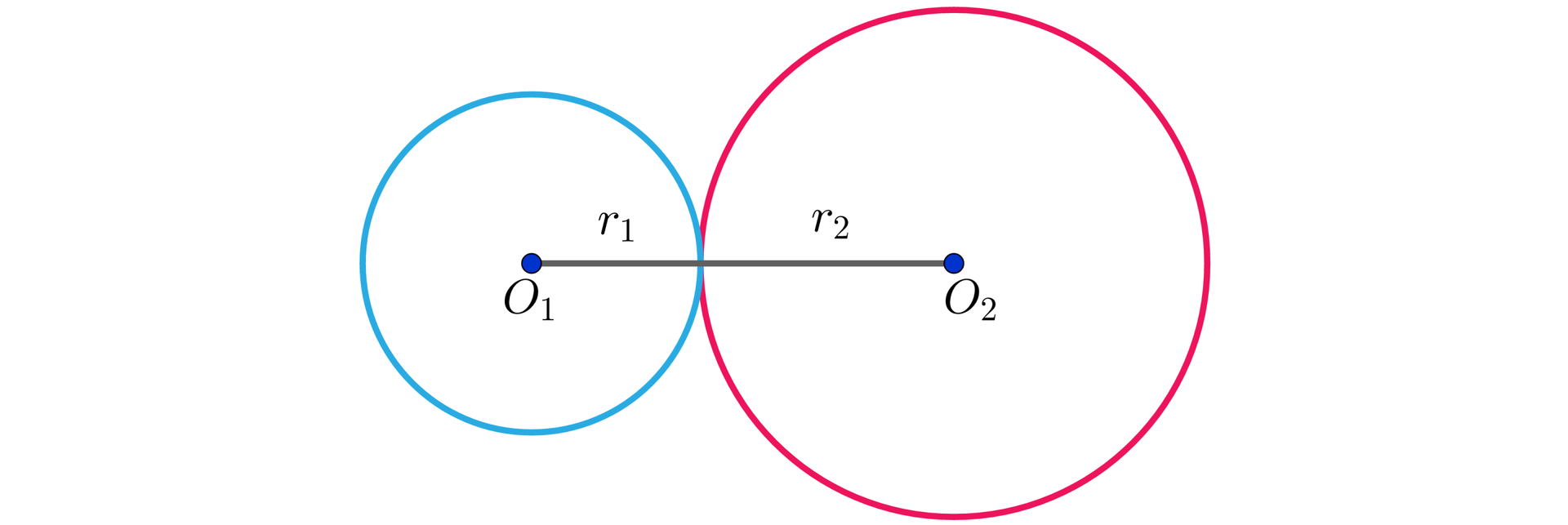
b) odległość środków okręgów jest równa różnicy długości ich promieni: , . Okręgi takie nazywamy stycznymi wewnętrznie.
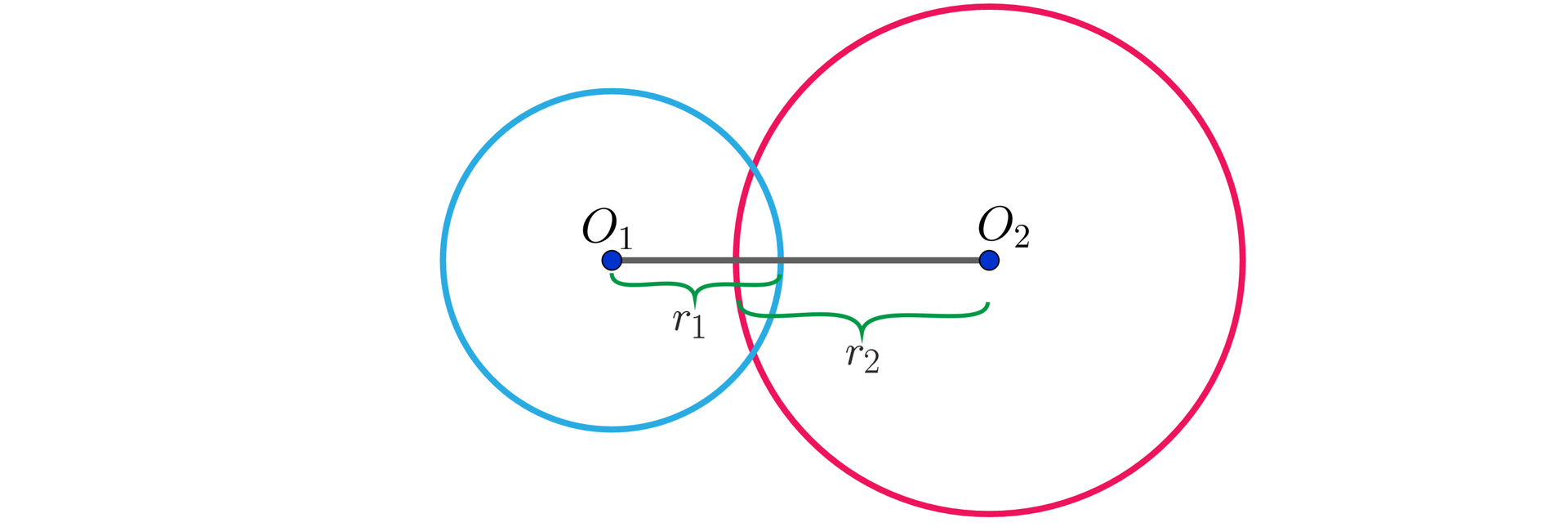
3. Okręgi mają dwa punkty wspólne gdy:
odległość między ich środkami jest mniejsza od sumy długości promieni i jednocześnie większa od różnicy długości tych promieni:
, .
Takie okręgi nazywamy okręgami przecinającymi się.
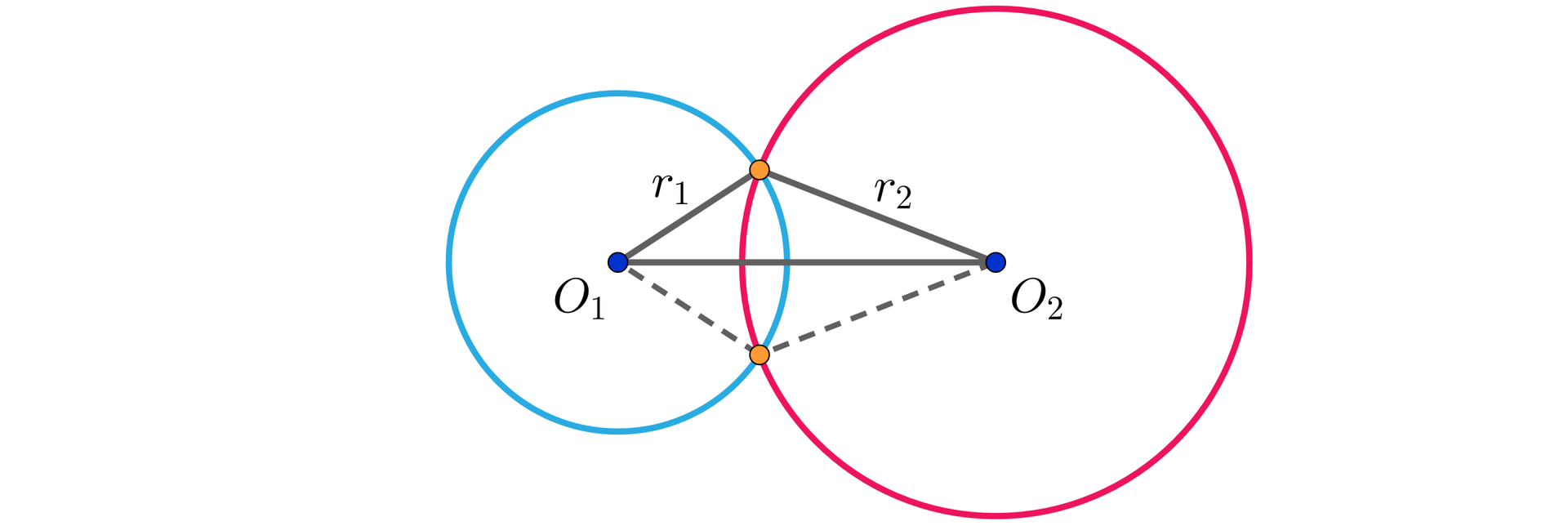
Zauważmy, że punkty wspólne przecinających się okręgów są symetryczne względem prostejsymetryczne względem prostej przechodzącej przez środki tych okręgów:
Określimy liczbę punktów wspólnych okręgów o promieniach długości i , których odległość między środkami wynosi .
Rozwiązanie
Zauważmy, że , zaś: .
Ponieważ spełniony jest warunek , to okręgi mają punkty wspólne.
Określimy liczbę punktów wspólnych okręgów o równaniach: i .
Rozwiązanie
Okrąg o równaniu ma środek w punkcie i promień długości .
Okrąg o równaniu ma środek w punkcie i promień długości .
Obliczamy odległość środków tych okręgów:
.
Wyznaczamy sumę i różnicę długości promieni tych okręgów:
,
.
Stąd: i .
Okręgi mają zatem punkty wspólne.
Mamy dany okrąg o środku w punkcie i promieniu długości . Okrąg o środku w punkcie i promieniu długości ma z danym okręgiem punkt wspólny. Wyznaczymy .
Rozwiązanie
Okręgi mają punkt wspólny, jeśli odległość ich środków jest równa sumie lub różnicy długości ich promieni.
Zatem: lub .
Wyznaczymy odległość środków okręgów:
.
Rozwiążemy równania:
(1) i (2) .
(1)
lub .
(2)
lub .
Zatem okrąg o środku w punkcie i promieniu długości ma z okręgiem o środku w punkcie i promieniu długości jeden punkt wspólny, jeśli lub , lub , lub
Wyznaczymy długość promienia okręgu o środku w punkcie tak, aby miał punkty wspólne z okręgiem o równaniu .
Rozwiązanie
Równanie okręgu możemy zapisać następująco: .
Równanie okręgu : doprowadzamy do postaci .
Po przekształceniach: otrzymujemy równanie okręgu postaci .
Jego środek ma współrzędne a promień ma długość .
Obliczamy odległość środków tych okręgów:
.
Okręgi i mają się przecinać, więc musi być spełniony warunek .
Zatem .
Warunek ten możemy zapisać za pomocą układu nierówności
Ponieważ długość promienia przyjmuje tylko wartości dodatnie, to dodajemy jeszcze warunek .
Mamy zatem
co oznacza, że okręgi i mają punkty wspólne, gdy .
Dane są dwa okręgi: o promieniu , styczny do osi w początku układu współrzędnych i o promieniu , styczny do osi w punkcie . Napiszemy równania tych okręgów oraz wyznaczymy współrzędne ich punktów wspólnych.
Rozwiązanie
Okrąg o równaniu jest styczny do osi w punkcie zatem: , czyli . Okrąg jest styczny do osi , stąd odległość środka okręgu od tej prostej jest równa promieniowi okręgu .
Korzystając ze wzoru na odległość środka okręgu od prostej mamy:
.
Rozwiązaniem równania są dwie liczby lub .
Z warunku wyznaczamy : . Dla i otrzymujemy .
Są zatem dwa okręgi o promieniu styczne do osi w początku układu współrzędnych:
: oraz : .
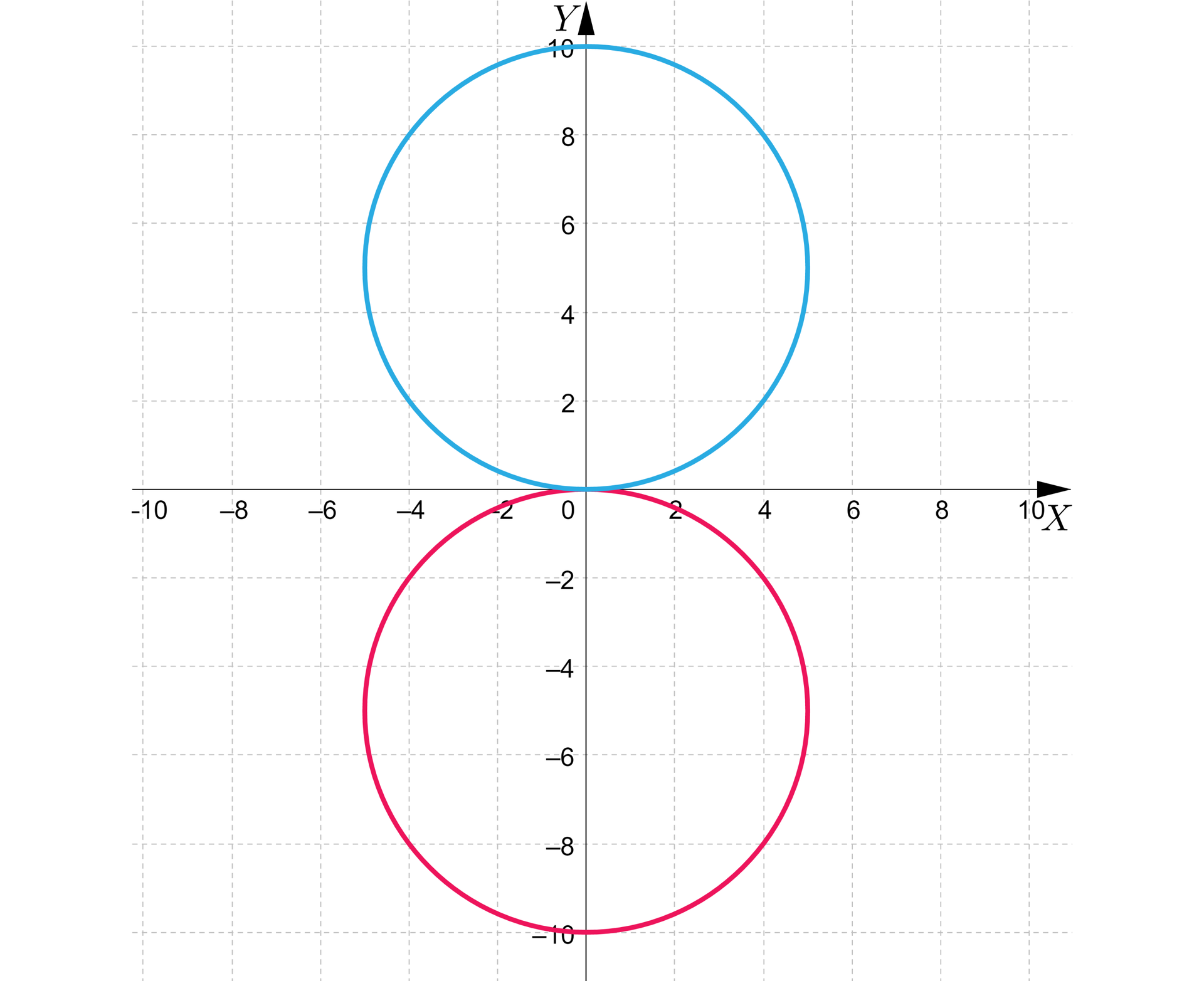
Te okręgi są styczne zewnętrznie, punktem styczności jest punkt .
Okrąg o równaniu jest styczny do osi w punkcie , zatem punkt leży na okręgu: , czyli .
Ponieważ okrąg ten jest styczny do osi , to odległość środka okręgu od tej prostej jest równa promieniowi okręgu .
Korzystając ze wzoru na odległość środka okręgu od prostej mamy:
.
Rozwiązaniem równania są dwie liczby: lub .
Z warunku mamy .
Dla lub otrzymujemy równanie , stąd .
Są zatem dwa okręgi o promieniu styczne do osi w punkcie :
: lub : .
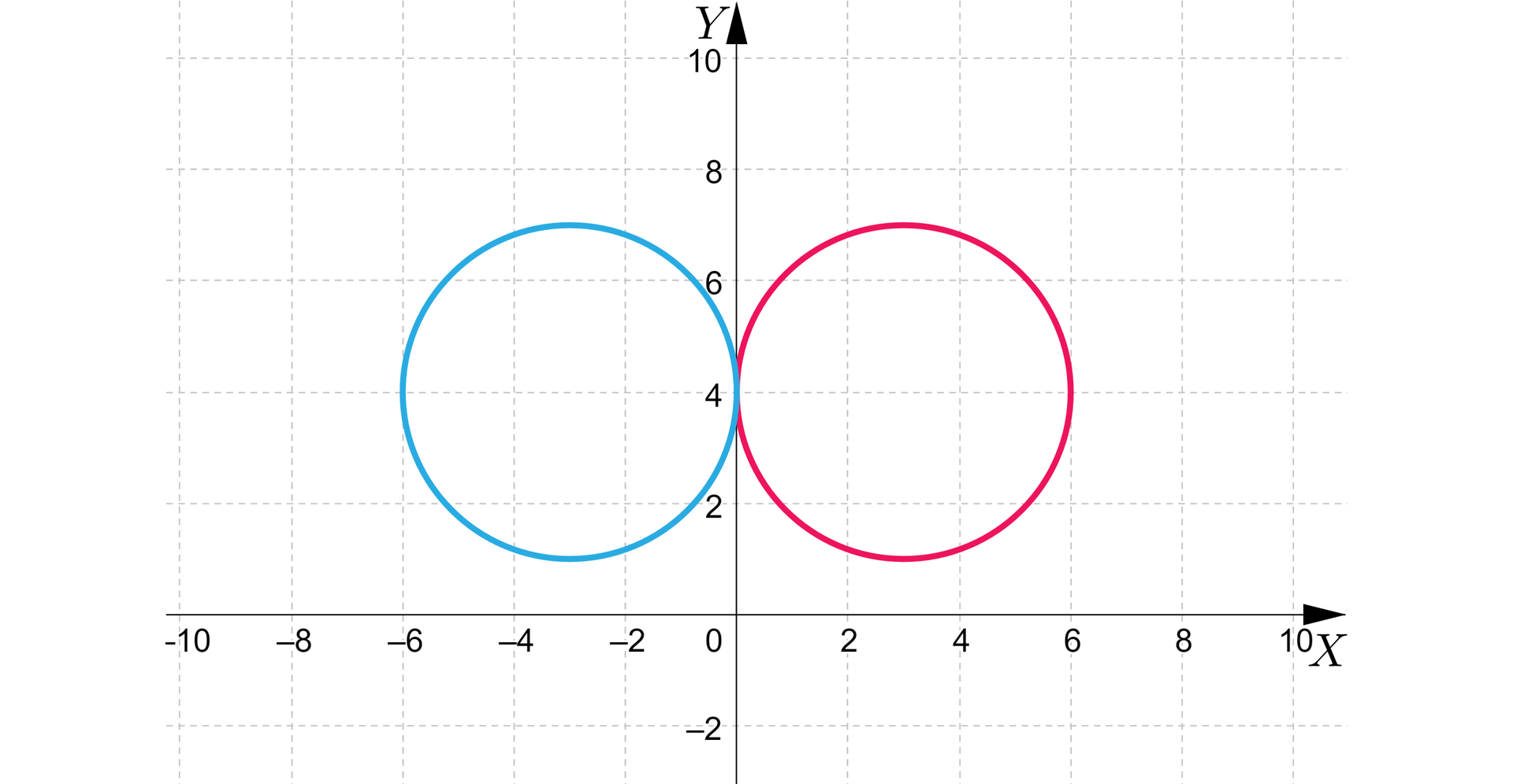
Te okręgi są styczne zewnętrznie a ich punktem styczności jest punkt .
Wyznaczymy teraz punkty przecięcia okręgu z okręgiem . Te okręgi się przecinają bo odległość środków tych okręgów spełnia warunek .
Aby znaleźć punkty przecięcia tych okręgów musimy rozwiązać układ równań:
.
Równanie po przekształceniach przyjmuje postać .
Równanie po przekształceniach jest postaci .
Rozwiązujemy zatem układ równań:
.
Odejmujemy stronami równania i otrzymujemy:
,
stąd
.
Po podstawieniu do równania otrzymujemy , co daje: , a stąd .
Wyróżnik trójmianu kwadratowego , istnieją więc dwa rozwiązania tego równania.
lub .
Dla : .
Dla : .
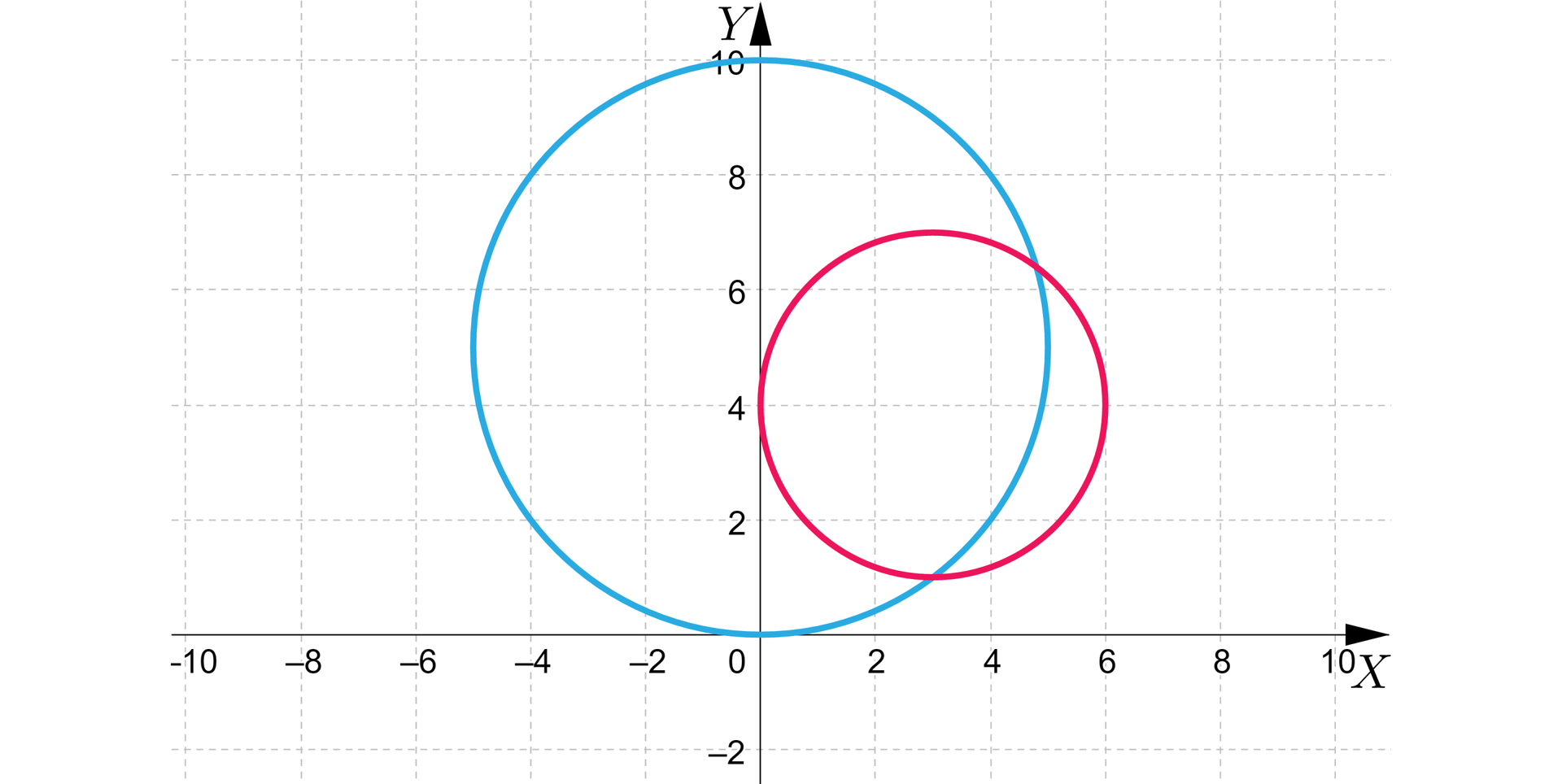
Okręgi i przecinają się w punktach i .
Wyznaczymy teraz punkty przecięcia okręgu : z okręgiem : . Te okręgi się przecinają bo odległość środków tych okręgów spełnia warunek .

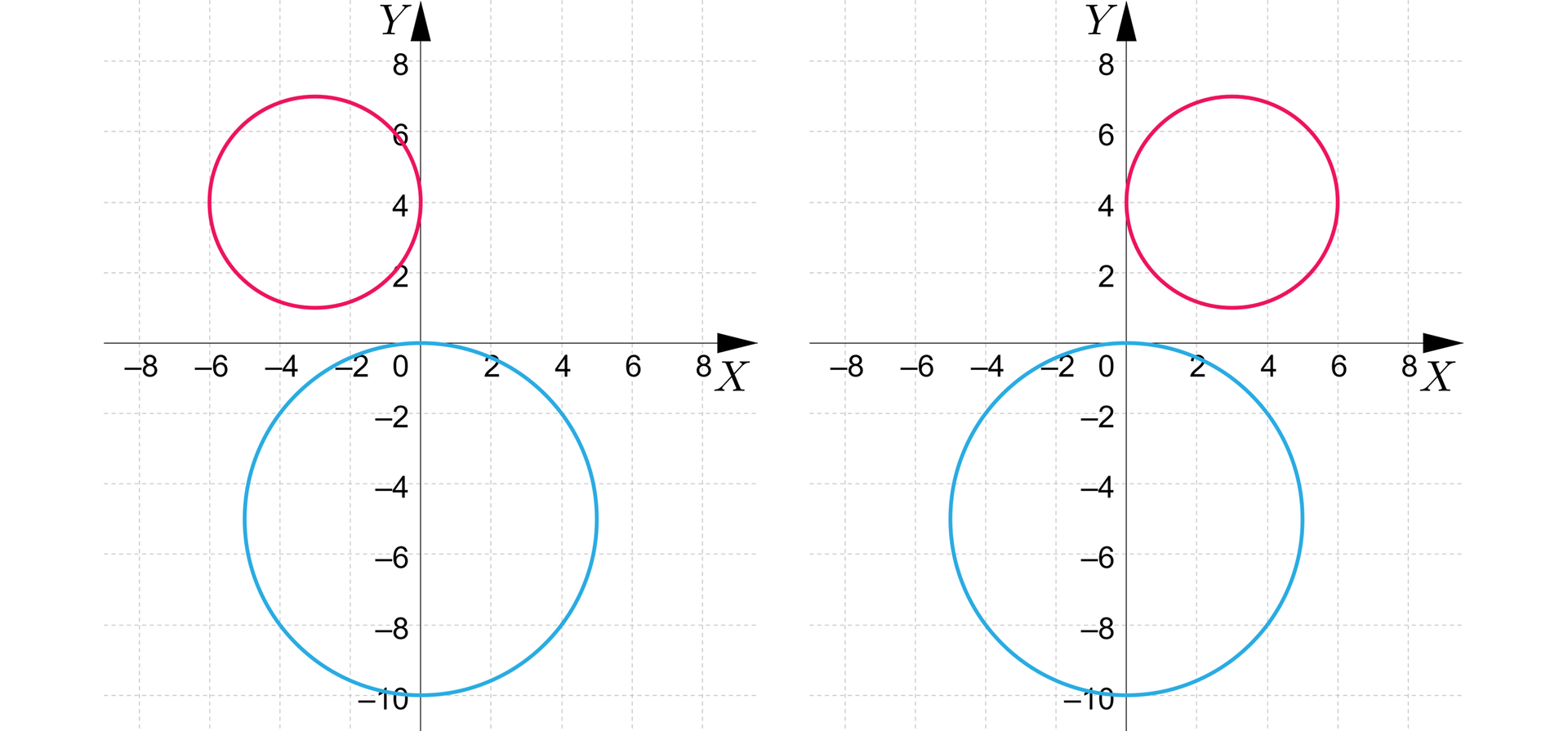
Ponieważ okręgi i , oraz okrąg , są symetryczne względem osi , to punkty przecięcia okręgów i z okręgiem są również symetryczne względem osi .
W związku z tym, jeśli okręgi i przecinają się w punktach i to okręgi i przecinają się w punktach i .
Okręgi i są rozłączne bo odległość środków tych okręgów spełnia warunek . Analogicznie - rozłączne są okręgi i .
Słownik
zbiór wszystkich punktów płaszczyzny, których odległość od punktu jest równa
leżą po przeciwnych stronach tej prostej i w równych od niej odległościach