Przeczytaj

W materiale wykorzystamy układy równań kwadratowych do rozwiązywania problemów matematycznych takich jak:

wyznaczanie równania okręgu na płaszczyźnie kartezjańskiej,

badanie wzajemnego położenia dwóch okręgów na płaszczyźnie kartezjańskiej,

znajdowanie wartości parametrów, dla których układ równań kwadratowych ma określoną liczbę rozwiązań,

wyznaczanie współrzędnych punktu, który jest odległy o zadaną długość od ustalonych punktów.

Już wiesz

W tym materiale będziemy rozpatrywać układy równań kwadratowych postaci :

\{\begin{cases} x^{2} + y^{2} + a x + b y = c \\ x^{2} + y^{2} + d x + e y = f \end{cases}

w którym oba równania są stopnia drugiego oraz $a, b, c, d, e, f \in ℝ$
i $x, y \in ℝ$ .

Omówimy sytuacje, w których układ równań:

może mieć nieskończenie wiele rozwiązań,

może mieć dokładnie dwa rozwiązania,

może mieć dokładnie jedno rozwiązanie,

może nie mieć rozwiązania.

Jeśli taki układ równań ma jedno rozwiązanie, to jest nim para liczb $(x, y)$ , która odpowiada współrzędnym odpowiedniego punktu na płaszczyźnie kartezjańskiej.

Na płaszczyźnie kartezjańskiej za pomocą równania kwadratowego możemy opisać równanie okręgu w postaci kanonicznej:

{(x - a)}^{2} + {(y - b)}^{2} = r^{2}

gdzie:
$S = (a, b)$ – środek okręgu,
$r$ – promień okręgu.

Przykład 1

Obliczymy odległość na płaszczyźnie kartezjańskiej pomiędzy punktami, których współrzędne są rozwiązaniami układu równań:

$\{\begin{cases} x^{2} + y^{2} = 5 \\ x^{2} - 4 x + y^{2} = 5 \end{cases}$ .

Rozwiązanie:

Jeżeli odejmiemy równania stronami, to $- 4 x = 0$ .

Wobec tego $x = 0$ .

Jeżeli $x = 0$ podstawimy do pierwszego równania, to $y^{2} = 5$ .

Zatem $y = - \sqrt{5}$ lub $y = \sqrt{5}$ .

Wobec tego rozwiązaniem układu równań są liczby, odpowiadające współrzędnym punktów $(0, - \sqrt{5})$ i $(0, \sqrt{5})$ .

Do wyznaczenia odległości między punktami $A = (x_{1}, y_{1})$ i $B = (x_{2}, y_{2})$ wykorzystamy następujący wzór:

$\sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ .

Wobec tego odległość pomiędzy wyznaczonymi punktami wynosi:

$\sqrt{{(0 - 0)}^{2} + {(\sqrt{5} - {(- \sqrt{5})}^{})}^{2}} = 2 \sqrt{5}$ .

Przykład 2

Określimy liczbę rozwiązań układu równań $\{\begin{cases} x^{2} + y^{2} = m \\ x^{2} - x + y^{2} - y = 0 \end{cases}$ , w zależności od wartości parametru $m$ .

Rozwiązanie:

Jeżeli zastosujemy metodę podstawiania, to rozwiązujemy równanie:

$m - x - y = 0$ , zatem $y = m - x$ .

Otrzymaną zależność podstawiamy do pierwszego równania:

$x^{2} + {(m - x)}^{2} = m$

$x^{2} + m^{2} - 2 m x + x^{2} - m = 0$ .

Po uporządkowaniu rozwiązujemy równanie $2 x^{2} - 2 m x + m^{2} - m = 0$ .

Zauważmy, że otrzymaliśmy równanie kwadratowe, zatem liczba jego rozwiązań, a tym samym układu równań, zależy od wartości wyróżnika.

Obliczamy wartość wyróżnika:

$∆ = {(- 2 m)}^{2} - 4 \cdot 2 \cdot (m^{2} - m) = 4 m^{2} - 8 m^{2} + 8 m = - 4 m^{2} + 8 m$ .

Układ równań ma dwa rozwiązania, gdy $∆ > 0$ .

Zatem $- 4 m^{2} + 8 m > 0$ , gdy $m \in (0, 2)$ .

Układ równań ma jedno rozwiązanie, gdy $∆ = 0$ .

Zatem $- 4 m^{2} + 8 m = 0$ , gdy $m \in \{0, 2\}$ .

Układ równań nie ma rozwiązania, gdy $∆ < 0$ .

Zatem $- 4 m^{2} + 8 m < 0$ , gdy $m \in (- \infty, 0) \cup (2, \infty)$ .

Przykład 3

Wyznaczymy równanie okręgu na płaszczyźnie kartezjańskiejrównanie okręgu na płaszczyźnie kartezjańskiej, do którego należą punkty o współrzędnych $(0, 5)$ oraz $(8, - 1)$ , a promień $r$ ma długość $5$ .

Rozwiązanie:

Korzystamy z równania okręgu postaci ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ i rozwiązujemy układ równań:

$\{\begin{cases} {(0 - a)}^{2} + {(5 - b)}^{2} = 25 \\ {(8 - a)}^{2} + {(- 1 - b)}^{2} = 25 \end{cases}$ .

Po przekształceniu układ równań zapisujemy w postaciach:

$\{\begin{cases} a^{2} + 25 - 10 b + b^{2} = 25 \\ 64 - 16 a + a^{2} + 1 + 2 b + b^{2} = 25 \end{cases}$ ,

$\{\begin{cases} a^{2} - 10 b + b^{2} = 0 \\ a^{2} + b^{2} - 16 a + 2 b = - 40 \end{cases}$ .

Po odjęciu równań stronami otrzymujemy równanie $12 b - 16 a = - 40$ , czyli $a = \frac{3 b + 10}{4}$ .

Po podstawieniu powyższej zależności do pierwszego równania, rozwiązujemy równanie:

${(\frac{3 b + 10}{4})}^{2} + b^{2} - 10 b = 0$

$b^{2} - 4 b + 4 = 0$ , czyli $b = 2$ .

Wobec tego $a = \frac{3 \cdot 2 + 10}{4} = 4$ .

Zatem równanie okręgu jest określone za pomocą wzoru ${(x - 4)}^{2} + {(y - 2)}^{2} = 25$ .

Przykład 4

Obliczymy iloczyn współrzędnych punktów, w których przecinają się okręgi określone równaniami ${(x + 2)}^{2} + y^{2} = 4$ oraz ${(x + 1)}^{2} + {(y - 2)}^{2} = 1$ .

Rozwiązanie:

Do wyznaczenia współrzędnych punktów wspólnych, rozwiązujemy układ równań:

$\{\begin{cases} {(x + 2)}^{2} + y^{2} = 4 \\ {(x + 1)}^{2} + {(y - 2)}^{2} = 1 \end{cases}$ .

Układ ten zapisujemy w postaci

$\{\begin{cases} x^{2} + 4 x + 4 + y^{2} = 4 \\ x^{2} + 2 x + 1 + y^{2} - 4 y + 4 = 1 \end{cases}$ ,

$\{\begin{cases} x^{2} + 4 x + y^{2} = 0 \\ x^{2} + 2 x + y^{2} - 4 y + 4 = 0 \end{cases}$ .

Jeżeli od pierwszego równania odejmiemy stronami drugie równanie, to otrzymujemy równanie $4 x - 2 x + 4 y - 4 = 0$ , czyli $x = 2 - 2 y$ .

Otrzymaną zależność podstawiamy do pierwszego równania i rozwiązujemy równanie:

${(2 - 2 y + 2)}^{2} + y^{2} = 4$ ,

$5 y^{2} - 16 y + 12 = 0$ .

Zatem $y = \frac{6}{5}$ oraz $y = 2$ .

Odpowiadające im wartości $x$ wynoszą:

$x = - \frac{2}{5}$ oraz $x = - 2$ .

Zatem okręgi przecinają się w punktach o współrzędnych $(- \frac{2}{5}, \frac{6}{5})$ oraz $(- 2, 2)$ .

Wobec tego iloczyn współrzędnych tych punktów wynosi:

$(- \frac{2}{5}) \cdot \frac{6}{5} \cdot (- 2) \cdot 2 = \frac{48}{25} = 1 \frac{23}{25}$ .

Przykład 5

Obliczymy pole trójkąta, którego dwa wierzchołki są punktami, których współrzędne spełniają układ równań $\{\begin{cases} x^{2} + 2 x + y^{2} - 24 = 0 \\ x^{2} + 2 x + y^{2} - 8 y + 8 = 0 \end{cases}$ , a trzeci wierzchołek ma współrzędne $(2, 6)$ .

Rozwiązanie:

Rozwiązujemy układ równań:

$\{\begin{cases} x^{2} + 2 x + y^{2} - 24 = 0 \\ x^{2} + 2 x + y^{2} - 8 y + 8 = 0 \end{cases}$ .

Jeżeli od drugiego równania odejmiemy stronami pierwsze równanie, to otrzymujemy zależność $- 8 y + 8 + 24 = 0$ .

Wobec tego $y = 4$ oraz

$x^{2} + 2 x + 4^{2} - 8 \cdot 4 + 8 = 0$ ,

$x^{2} + 2 x - 8 = 0$ .

Zatem $x = - 4$ oraz $x = 2$ .

Czyli szukane punkty to $(- 4, 4)$ oraz $(2, 4)$ .

Jeżeli zaznaczymy wierzchołki trójkąta w układzie współrzędnych, to otrzymujemy trójkąt prostokątny.

RJ2E8zzxrmkRO

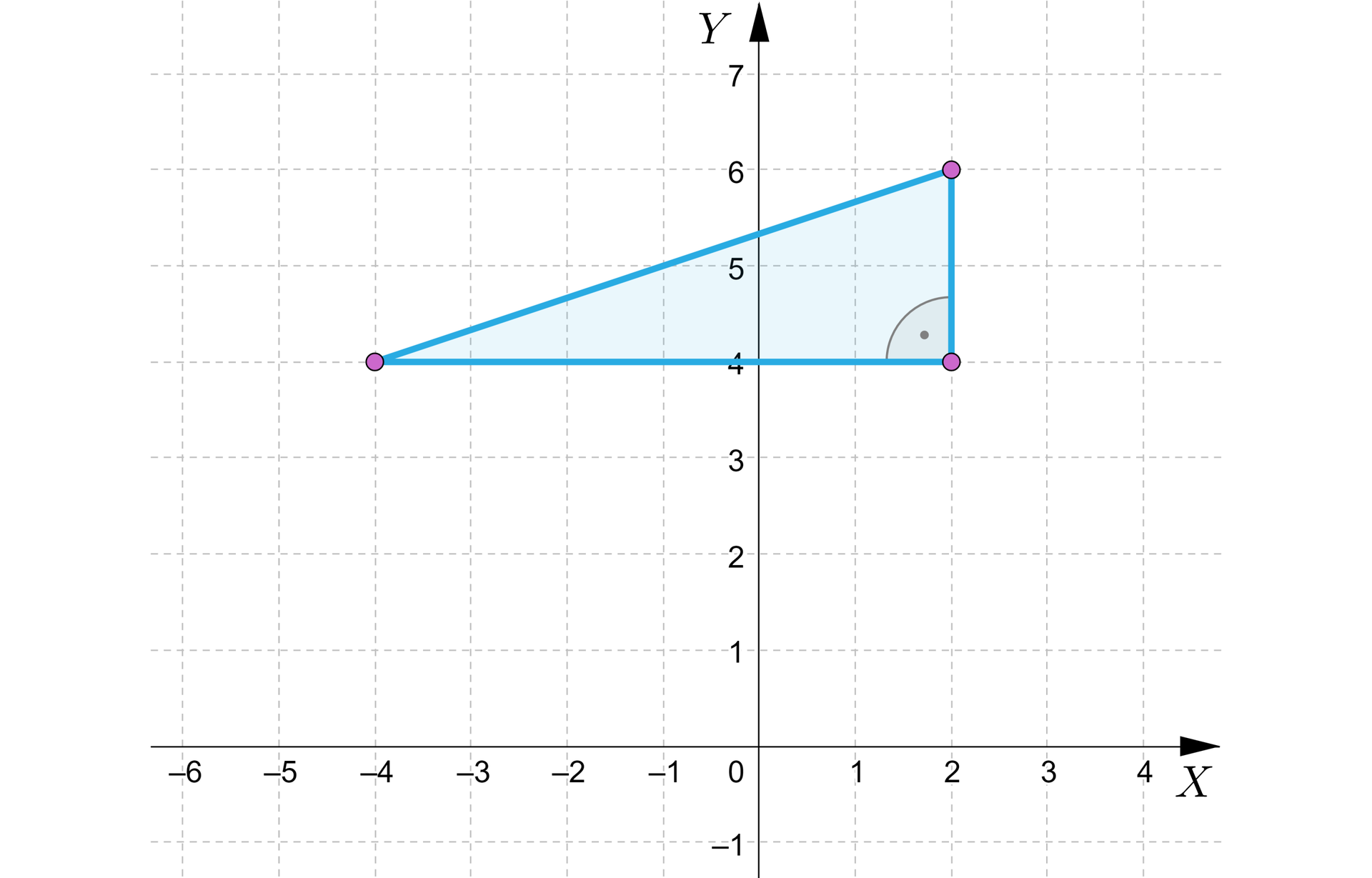
Grafika przedstawia układ współrzędnych z poziomą osią x od minus sześciu do czterech i pionową osią y od minus jeden do siedmiu. Na płaszczyźnie znajduje się trójkąt prostokątny. Wierzchołki trójkąta są zaznaczone zamalowanymi kropkami o współrzędnych kolejno: początek nawiasu, minus 4, 4, zamknięcie nawiasu, początek nawiasu, 2, 4, zamknięcie nawiasu, początek nawiasu, 2, 6, zamknięcie nawiasu. Przy punkcie początek nawiasu, 2, 4, zamknięcie nawiasu zaznaczony został kąt prosty.

Zatem pole tego trójkąta jest równe:

$P = \frac{1}{2} \cdot 6 \cdot 2 = 6$ .

Słownik:

postać kanoniczna równania okręgu na płaszczyźnie kartezjańskiej

równanie postaci

{(x - a)}^{2} + {(y - b)}^{2} = r^{2}

gdzie:
$S = (a, b)$ – środek okręgu,
$r$ – promień okręgu

Wprowadzenie

Gra edukacyjna

Słownik: