Cosinusem kąta ostrego w trójkącie prostokątnym nazywamy iloraz długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.

RPVx3I3OAOB8b

Rysunek przedstawia trójkąt prostokątny o podstawie $a$, która jest jednocześnie bokiem $CB$, o pionowej przyprostokątnej $b$, która jest bokiem $AC$ oraz o przeciwprostokątnej $c$, która jest bokiem $AB$. Na rysunku zaznaczono również kąty wewnętrzne trójkąta. Przy wierzchołku $C$ oznaczono kąt prosty, przy wierzchołku $B$ oznaczono kąt $\beta$, a przy wierzchołku $A$ oznaczono kąt $\alpha$.

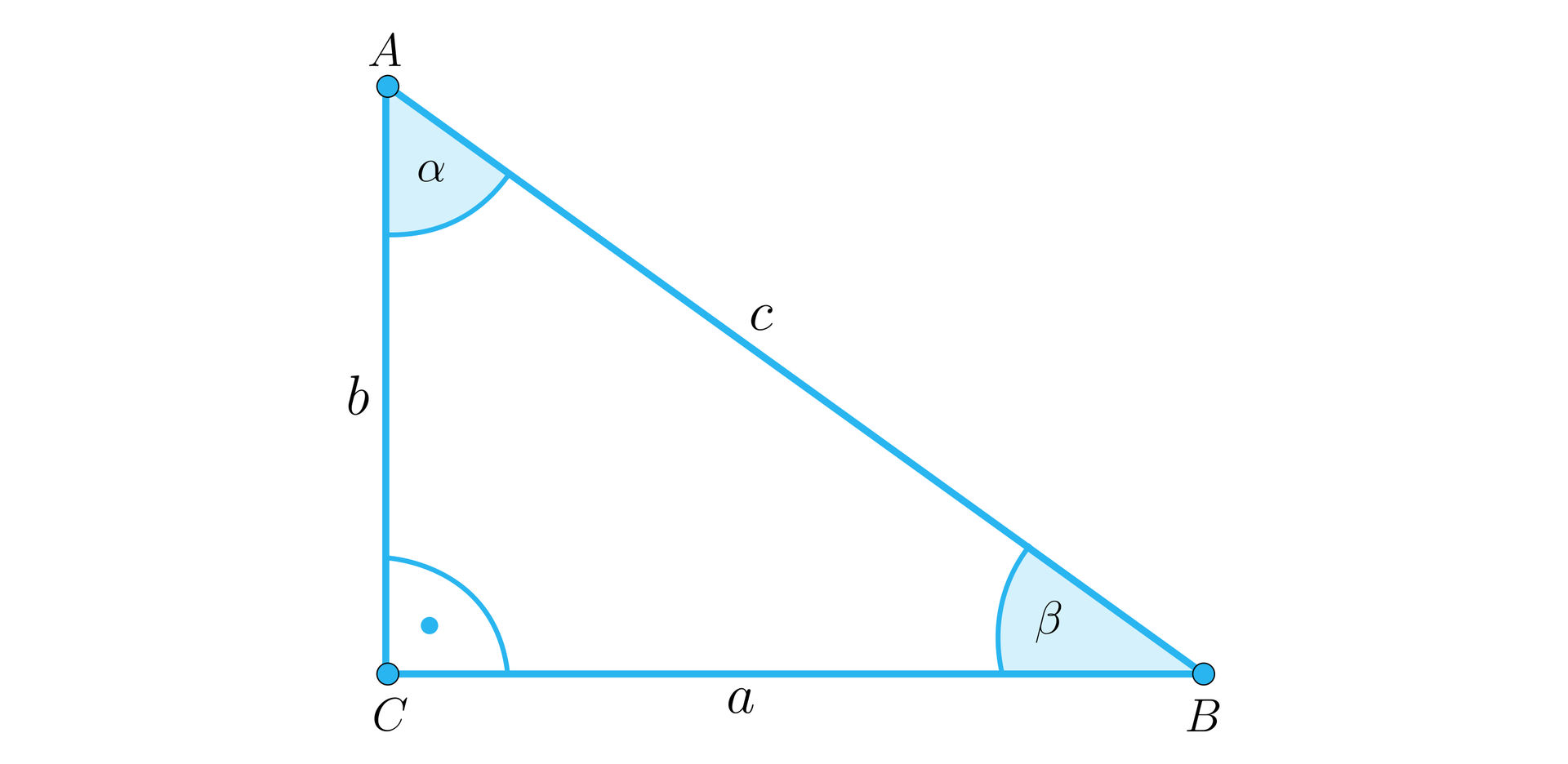
Do oznaczenia funkcji cosinus używa się skrótu cos.

Wzór funkcji cosinus zapisujemy słownie:

$\mathrm{cosinus} \mathrm{kąta} \mathrm{ostrego}=\frac{\mathrm{długość} \mathrm{przyprostokątnej} \mathrm{leżącej} \mathrm{przy} \mathrm{kącie}}{\mathrm{długość} \mathrm{przeciwprostokątnej}}$

Zapisując za pomocą symboli matematycznych, mamy, że:

$\cos \alpha =\frac{b}{c}$,

$\cos \beta =\frac{a}{c}$.

Wyznaczymy wartości cosinusów kątów ostrych w trójkącie prostokątnym z rysunku.

R1SGVgJ5FSZVb

Rysunek przedstawia trójkąt prostokątny o podstawie o długości $6$ i o pionowej przyprostokątnej o długości $3$. Na rysunku zaznaczono również kąty wewnętrzne trójkąta. Kąt prosty między opisanymi wyżej bokami, kąt $\beta$ między przeciwprostokątną a podstawą o długości $6$ oraz kąt $\alpha$ między przyprostokątną a bokiem o długości $3$.

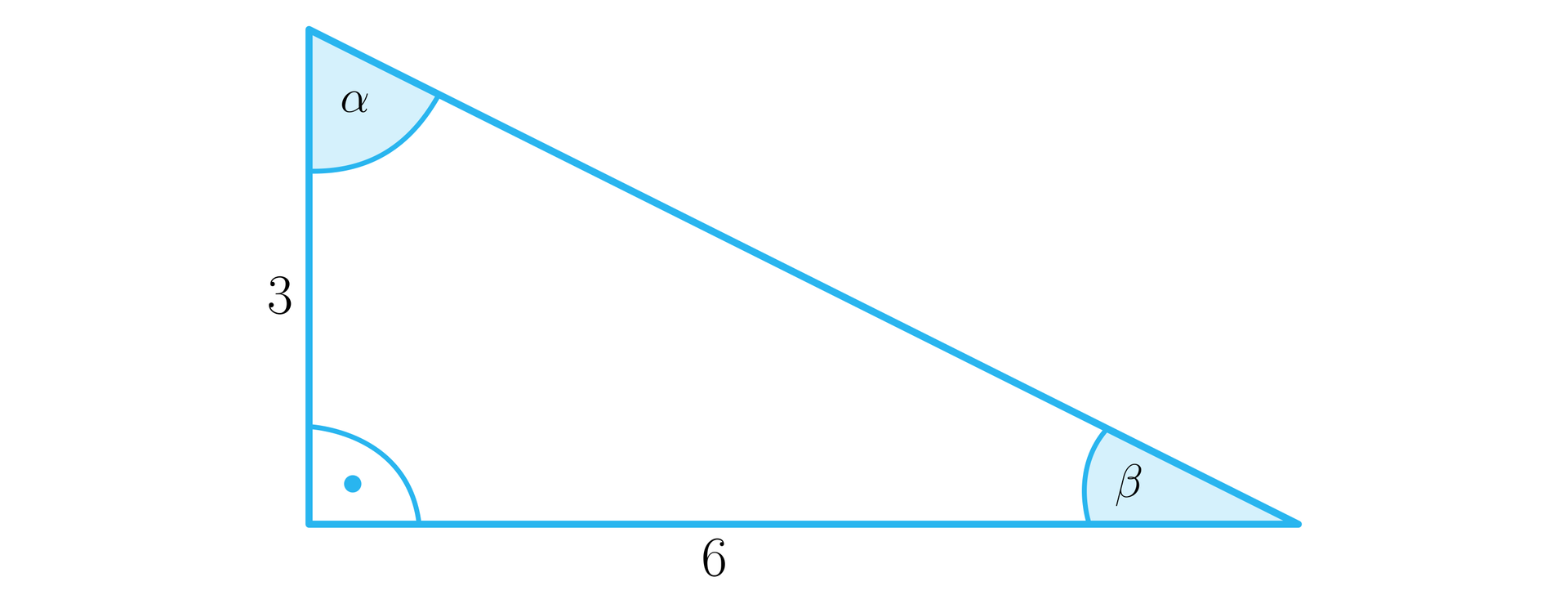
Rozwiązanie:

Oznaczmy długość przeciwprostokątnej jako $x$.

Z twierdzenia Pitagorasa mamy, że $3^2+6^2=x^2$.

Z równania wynika, że $x^2=45$, zatem $x=\sqrt{45}=3\sqrt{5}$ lub $x=-\sqrt{45}=-3\sqrt{5}$.

Ponieważ $x>0$, więc $x=\sqrt{45}=3\sqrt{5}$.

Z definicji funkcji cosinus otrzymujemy, że:

$\cos \alpha =\frac{3}{3\sqrt{5}}=\frac{\sqrt{5}}{5}$,

$\cos \beta =\frac{6}{3\sqrt{5}}=\frac{2\sqrt{5}}{5}$.

Wyznaczymy wartość cosinusa mniejszego kąta ostrego w trójkącie prostokątnym, jeżeli jedna przyprostokątna trójkąta ma długość $5$, a przeciwprostokątna długość $10$.

Rozwiązanie:

Narysujmy trójkąt prostokątny i wprowadźmy oznaczenia, jak na rysunku:

R5og477hgJKnH

Rysunek przedstawia trójkąt prostokątny o podstawie $x$, pionowej przyprostokątnej o długości $5$ oraz o przeciwprostokątnej o długości $10$. Na rysunku zaznaczono również kąty wewnętrzne trójkąta. Kąt prosty między podstawą a bokiem o długości $5$, kąt $\alpha$ między przeciwprostokątną a podstawą oraz kąt $\beta$ między przyprostokątną a bokiem o długości $5$.

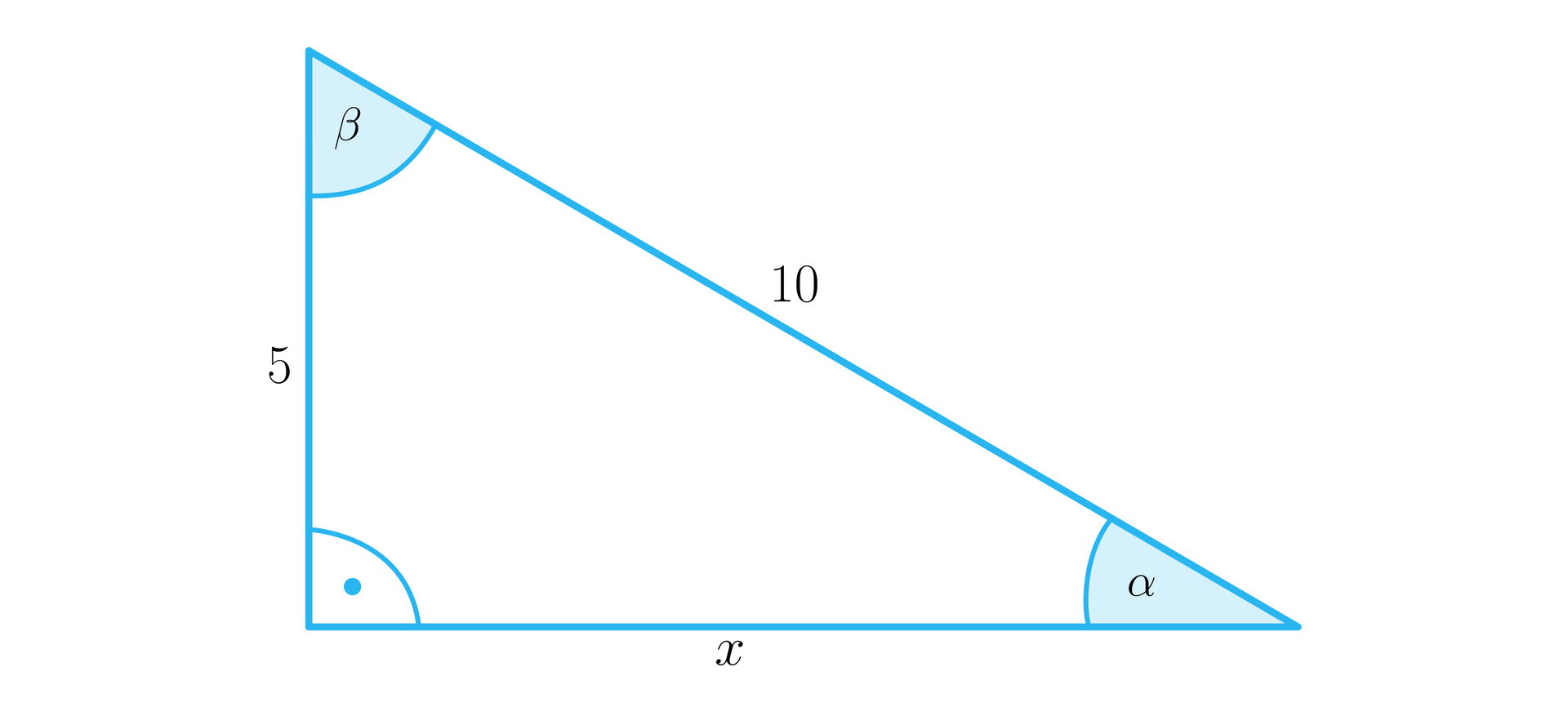
Rozwiązanie:

Niech $x$ oznacza długość drugiej przyprostokątnej. Wtedy, korzystając z twierdzenia Pitagorasa, rozwiązujemy równanie:

$x^2+5^2={10}^2$.

Zatem $x^2=75$, wobec tego

$x=5\sqrt{3}$ lub $x=-5\sqrt{3}$.

Ponieważ $x$ jest długością boku, zatem $x=5\sqrt{3}$.

W dowolnym trójkącie kąt o najmniejszej mierze leży naprzeciwko najkrótszego boku, zatem mniejszym kątem ostrym jest kąt o mierze $\alpha$.

Wobec tego

$\cos \alpha =\frac{5\sqrt{3}}{10}=\frac{\sqrt{3}}{2}$.

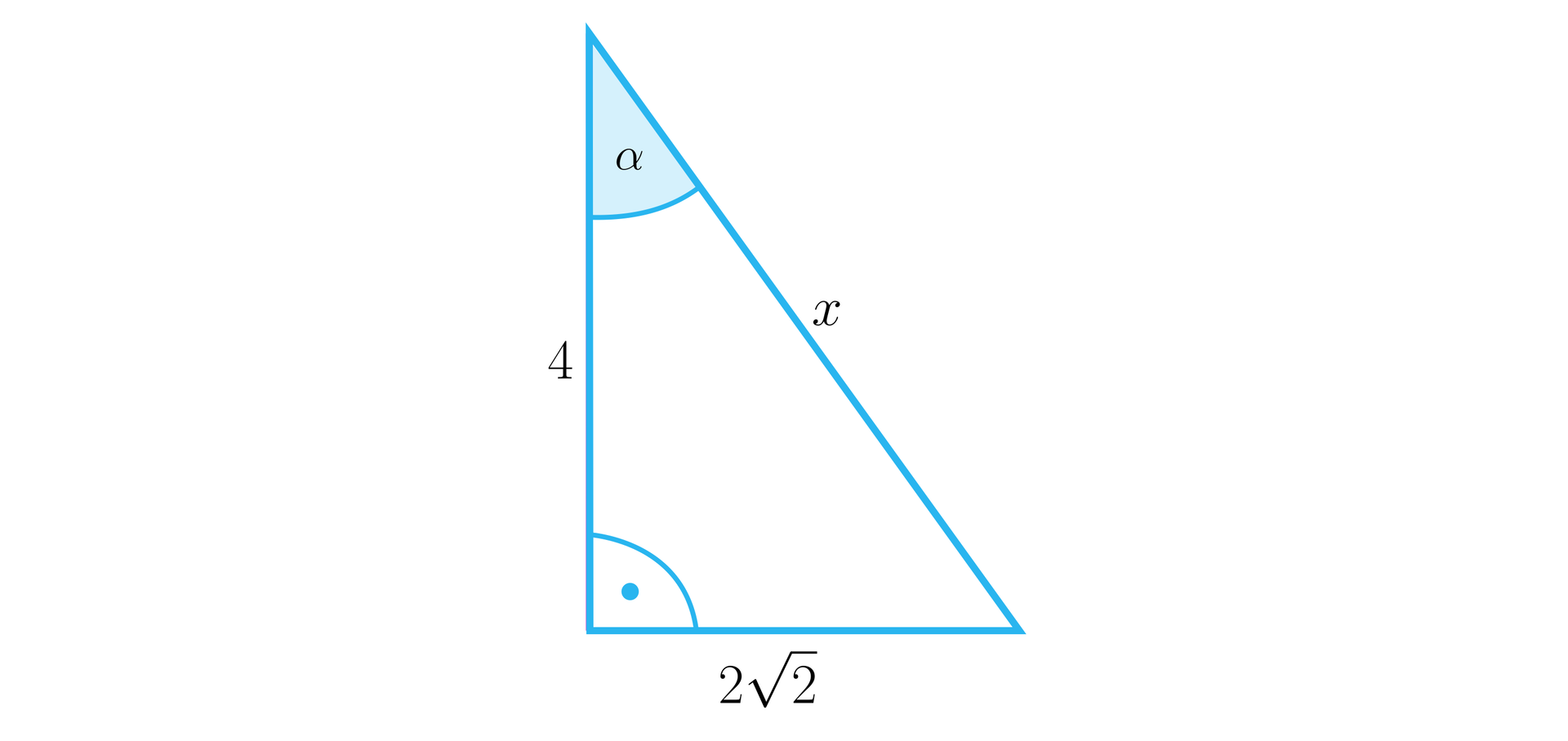
Obliczymy wartość wyrażenia $\sqrt{3-2{\cos }^2\alpha }$, jeżeli $\alpha$ jest kątem ostrym w trójkącie prostokątnym, leżącym przy dłuższej przyprostokątnej, wiedząc że krótsza przyprostokątna trójkąta ma długość $3\sqrt{3}$, a przeciwprostokątna ma długość $2\sqrt{15}$.

Rozwiązanie:

Narysujmy trójkąt prostokątny i wprowadźmy oznaczenia, jak na rysunku:

R1J2Il9PYnZC5

Rysunek przedstawia trójkąt prostokątny o podstawie $x$, pionowej przyprostokątnej o długości $3\sqrt{3}$ oraz o przeciwprostokątnej o długości $2\sqrt{15}$. Na rysunku zaznaczono również kąty wewnętrzne trójkąta. Kąt prosty między podstawą a bokiem o długości $3\sqrt{3}$, kąt $\alpha$ między przeciwprostokątną a podstawą oraz kąt $\beta$ między przyprostokątną a bokiem o długości $3\sqrt{3}$.

Rozwiązanie:

Niech $x$ oznacza długość dłuższej przyprostokątnej.

Wówczas, korzystając z twierdzenia Pitagorasa, zapisujemy i rozwiązujemy równanie:

$x^2+{\left(3\sqrt{3}\right)}^2={\left(2\sqrt{15}\right)}^2$.

Zatem $x^2=33$, czyli $x=\sqrt{33}$.

Dłuższa przyprostokątna ma długość $\sqrt{33}$, zatem kąt ostry leżący przy tym boku ma miarę $\alpha$.

Wobec tego:

$\cos \alpha =\frac{\sqrt{33}}{2\sqrt{15}}=\frac{\sqrt{495}}{30}$.

Wartość wyrażenia $\sqrt{3-2{\cos }^2\alpha }$ wynosi $\sqrt{3-2·{\left(\frac{\sqrt{495}}{30}\right)}^2}=\sqrt{3-2·\frac{495}{900}}=\sqrt{\frac{171}{90}}=\frac{\sqrt{190}}{10}$.

Wyznaczymy długości przyprostokątnych w trójkącie prostokątnym o przeciwprostokątnej długości $12$, jeżeli wiadomo, że cosinus jednego kąta ostrego jest trzy razy większy od cosinusa drugiego kąta ostrego.

RPVx3I3OAOB8b

Rysunek przedstawia trójkąt prostokątny o podstawie $a$, która jest jednocześnie bokiem $CB$, o pionowej przyprostokątnej $b$, która jest bokiem $AC$ oraz o przeciwprostokątnej $c$, która jest bokiem $AB$. Na rysunku zaznaczono również kąty wewnętrzne trójkąta. Przy wierzchołku $C$ oznaczono kąt prosty, przy wierzchołku $B$ oznaczono kąt $\beta$, a przy wierzchołku $A$ oznaczono kąt $\alpha$.

Z warunków zadania wynika, że $\cos \alpha =3\cos \beta$ oraz $c=12$.

Z trójkąta prostokątnego z rysunku mamy, że $\cos \alpha =\frac{b}{c}$ oraz $\cos \beta =\frac{a}{c}$.

Po podstawieniu do zależności $\cos \alpha =3\cos \beta$ mamy, że:

$\frac{b}{c}=3·\frac{a}{c}$, czyli $b=3a$.

Z twierdzenia Pitagorasa mamy, że $c^2=a^2+{\left(3a\right)}^2$, więc $c=\sqrt{10}a$.

Otrzymujemy równanie $12=\sqrt{10}a$, zatem $a=\frac{6\sqrt{10}}{5}$.

Zatem przyprostokątne mają długości:

$a=\frac{6\sqrt{10}}{5}$,

$b=3·\frac{6\sqrt{10}}{5}=\frac{18\sqrt{10}}{5}$.

W trójkącie równoramiennym podstawa ma długość $4\sqrt{2}$, a wysokość opuszczona na tę podstawę ma długość $4$. Obliczymy cosinus kąta pomiędzy wysokością tego trójkąta a ramieniem.

Rozwiązanie:

Narysujmy trójkąt równoramienny i wprowadźmy oznaczenia, jak na rysunku:

RLmnXSJFu5dQz

Rysunek przedstawia trójkąt równoramienny o podstawie o długości $4\sqrt{2}$ i ramieniu $x$. Z górnego wierzchołka upuszczono na podstawę wysokość o długości $4$ i oznaczono kąt prosty między wysokością a podstawą. Między wysokością a ramieniem $x$ zaznaczono kąt $\alpha$.

Do wyznaczenia wartości $\cos \alpha$ rozpatrujemy trójkąt prostokątny:

R1TpfR2pxLfAT

Rysunek przedstawia trójkąt prostokątny o podstawie o długości $2\sqrt{2}$ i przeciwprostokątnej $x$. Pionowa przyprostokątna ma długość $4$. W trójkącie oznaczono dwa kąty wewnętrzne. Kąt prosty między przyprostokątnymi o długościach $4$ oraz $2\sqrt{2}$ oraz kąt $\alpha$ między pionowym bokiem o długości $4$ a przeciwprostokątną.

Jeżeli przez $x$ oznaczymy długość przeciwprostokątnej tego trójkąta, to korzystając z twierdzenia Pitagorasa rozwiązujemy równanie:

${\left(2\sqrt{2}\right)}^2+4^2=x^2$.

Zatem $x^2=24$, czyli $x=2\sqrt{6}$.

Wobec tego

$\cos \alpha =\frac{4}{2\sqrt{6}}=\frac{2}{\sqrt{6}}=\frac{\sqrt{6}}{3}$.

Dany jest prostokąt o bokach długości $4$ i $8$. Wyznaczymy cosinusy kątów, jakie tworzy przekątna tego prostokąta z jego bokami.

Rozwiązanie:

Narysujmy prostokąt i wprowadźmy oznaczenia, jak na rysunku:

RRmtxuAhOjJvP

Rysunek przedstawia prostokąt, w którym poprowadzono przekątną, dzięki czemu utworzono trójkąt prostokątny o podstawie o długości $8$, przeciwprostokątnej $x$ i pionowej przyprostokątnej o długości $4$. W trójkącie oznaczono kąty wewnętrzne. Kąt prosty między przyprostokątnymi o długościach $4$ oraz $8$, kąt $\alpha$ między podstawą a przeciwprostokątną oraz kąt $\beta$ między przeciwprostokątną a bokiem o długości $4$ .

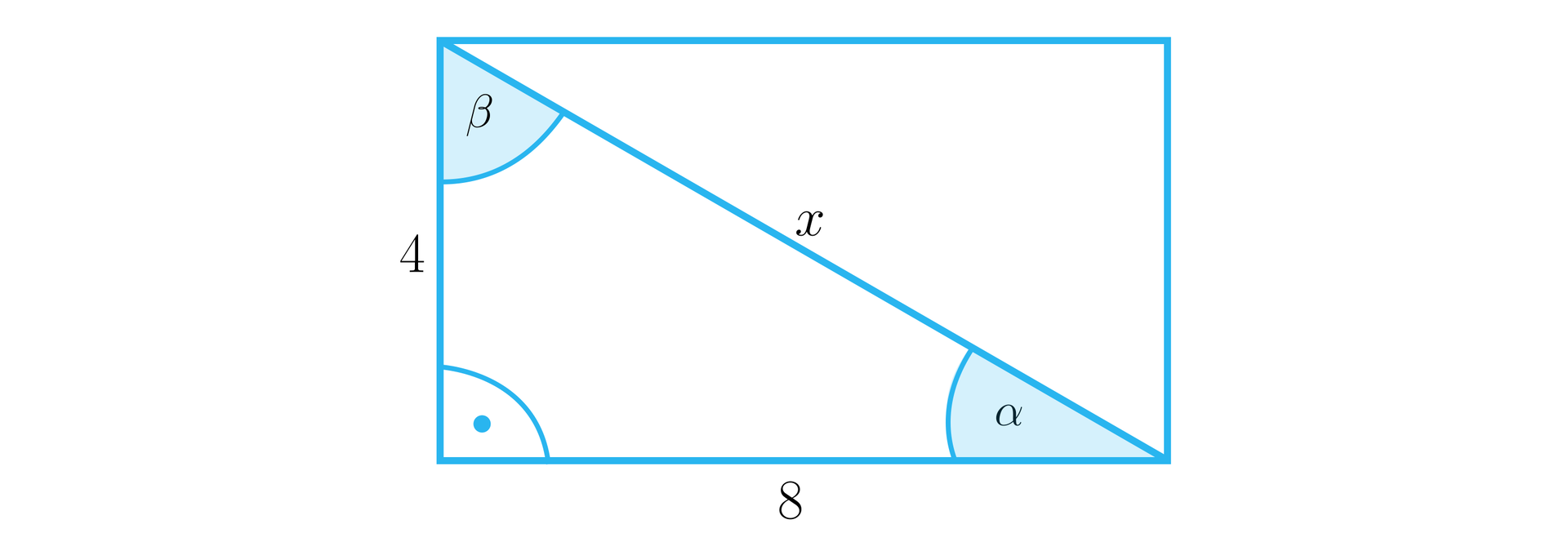
Zauważmy, że przekątna prostokąta dzieli go na dwa przystające trójkąty prostokątne.

Jeżeli długość przekątnej prostokąta oznaczymy jako $x$, to korzystając z twierdzenia Pitagora rozwiązujemy równanie:

$4^2+8^2=x^2$,

zatem

$x^2=80$

$x=4\sqrt{5}$.

Wobec tego:

$\cos \alpha =\frac{8}{4\sqrt{5}}=\frac{2\sqrt{5}}{5}$,

$\cos \beta =\frac{4}{4\sqrt{5}}=\frac{\sqrt{5}}{5}$.

iloraz długości przyprostokątnej leżącej przy kącie do długości przeciwprostokątnej