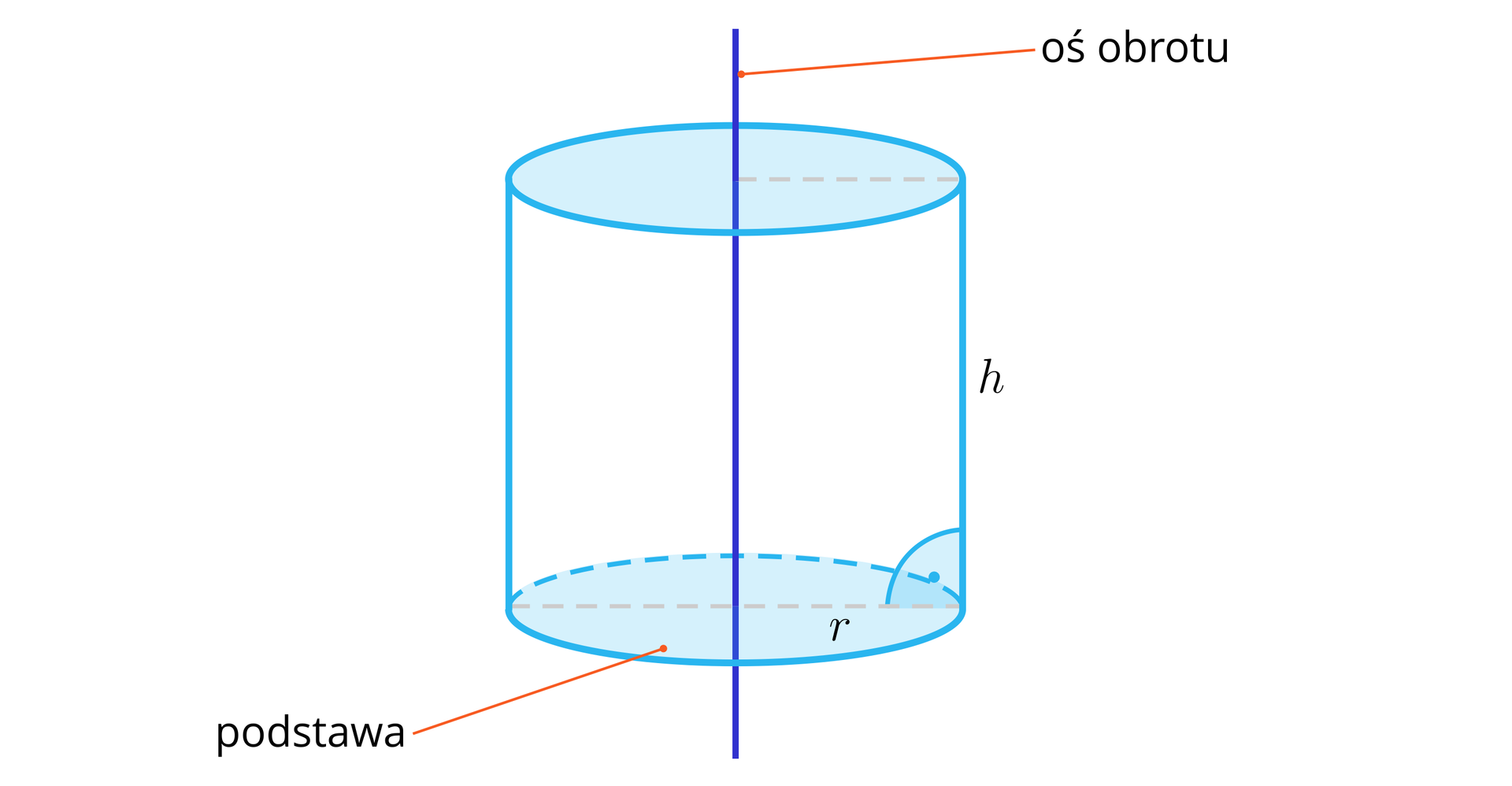
Walec jest bryłą obrotową, która powstaje przez obrót prostokąta dookoła osi zawierającej jeden z jego boków.

Niech $r$ będzie długością promienia podstawy walca, a $h$ jego wysokością.

RBJWbwDFqEnj4

Ilustracja przedstawia walec położony na podstawie o długości promienia r. Na ilustracji zaznaczona została także wysokość walca o długości h oraz jego oś obrotu przechodząca przez środek podstawy.

Obliczymy pole powierzchni całkowitej walca powstałego w wyniku obrotu prostokąta o wymiarach $12$ i $16$ wokół krótszego boku.

Rozwiązanie

Narysujmy walec i wprowadźmy odpowiednie oznaczenia.

RrMsq8Jpmy5zh

Ilustracja przedstawia walec położony na podstawie o długości promienia szesnaście i wysokości równej dwanaście. Na ilustracji utworzona została także nowa płaszczyzna wewnątrz bryły. Płaszczyzna ta jest prostokątem, pierwszy bok tej figury jest zawarty w osi obrotu o długości dwanaście, drugi natomiast w bocznej krawędzi figury. Dwa dłuższe boki są promieniami obu podstaw walca o długości szesnaście.

Jeżeli $r$ jest długością promienia podstawy walca, a $r$ długością jego wysokości, to:

$r=16$,

$h=12$.

Zatem pole powierzchni całkowitej tego walca wynosi:

$P_c=2\pi ·{16}^2+2\pi ·16·12=512\pi +384\pi =896\pi$.

Obliczymy pole powierzchnipole powierzchnipole powierzchni całkowitej walca, jeżeli obwód jego podstawy wynosi $16\pi$, a wysokość walca ma długość $6$.

Rozwiązanie

Narysujmy walec i wprowadźmy odpowiednie oznaczenia.

R1aJXLLXGNt0B

Ilustracja przedstawia walec położony na podstawie o długości promienia r. Zaznaczona została także wysokości h będąca jednocześnie prostopadła do promienia podstawy.

Z treści zadania mamy, że $h=6$. Obwód podstawy walcawalecwalca o promieniu $r$ obliczamy ze wzoru $L=2\pi r$, zatem do wyznaczenia wartości $r$ rozwiązujemy równanie:

$16\pi =2\pi ·r$, czyli $r=8$.

Wobec tego pole powierzchni całkowitej tego walca wynosi:

$P_c=2\pi r^2+2\pi rh$

$P_c=2\pi ·8^2+2\pi ·8·6=128\pi +96\pi =224\pi$.

Obliczymy długość promienia podstawy walca, gdy jego pole powierzchni całkowitej wynosi $42\pi$, a wysokość ma długość $4$.

Rozwiązanie

$P_c=42\pi$,

$h=4$.

Niech $r$ będzie długością promienia podstawy walca.

Do wyznaczenia wartości $r$ wykorzystamy wzór na pole powierzchni całkowitej walca:

$P_c=2\pi r^2+2\pi rh$.

Zatem:

$42\pi =2\pi ·r^2+2\pi ·r·4$

$42=2·r^2+2·r·4$

$r^2+4r-21=0$

$r_1=\frac{-4-10}{2}=-7<0$

$r_2=\frac{-4+10}{2}=3>0$.

Zatem promień podstawy walca jest równy $3$.

Obliczymy pole powierzchni całkowitej bryły o wymiarach, jak na rysunku.

RcggG4HZoUKLz

Ilustracja przedstawia dwa walce, pierwszy większy o średnicy podstawy równej dziesięć i wysokości o długości cztery. Drugi walec posiada średnice podstawy o długości sześć oraz wysokość o długości cztery. Oba walce są ze sobą połączone w taki sposób, że dolna podstawa mniejszego walca zawiera się w górnej podstawie większego walca. Bryła przypomina przycisk.

Rozwiązanie

Zauważmy, że bryła z rysunku składa się z dwóch walców.

Wprowadźmy następujące oznaczenia:
$r_1$ – długość promienia mniejszego walca,
$r_2$ – długość promienia większego walca,
$h_1$ – długość wysokości mniejszego walca,
$h_2$ – długość wysokości większego walca.

Z rysunku odczytujemy, że:

$r_1=3$,

$r_2=5$,

$h_1=h_2=4$.

Wobec tego pole powierzchni całkowitej tej bryły obliczymy ze wzoru:

$P_c=2\pi r_1·h_1+2\pi {r_2}^2+2\pi r_2·h_2$.

Zatem:

$P_c=2\pi ·3·4+2\pi ·5^2+2\pi ·5·4=24\pi +50\pi +40\pi =114\pi$.

W sześcian o przekątnej długości $9$ wpisano walec. Obliczymy pole powierzchni całkowitej tego walca.

Rozwiązanie

Narysujmy walec wpisany w sześcian i wprowadźmy oznaczenia, jak na rysunku.

R1HDs11WoiI9W

Ilustracja przedstawia walec o długości promienia podstawy r oraz wysokości h wpisanego w sześcian, którego krawędzie zostały oznaczone jako a. Wysokość walca h jest równa długości krawędzi sześcianu a oraz przechodzi przez środek ściany bocznej.

Zauważmy, że jeśli $a$ jest długością krawędzi sześcianu, $r$ długością promienia podstawy walca, a $h$ długością jego wysokości, to zachodzą następujące zależności:

$r=\frac{1}{2}a$ oraz $h=a$.

Ponieważ przekątna sześcianu ma długość $9$, zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$9=a\sqrt{3}$

$a=3\sqrt{3}$.

Zatem $r=\frac{1}{2}·3\sqrt{3}=\frac{3\sqrt{3}}{2}$ oraz $h=3\sqrt{3}$.

Wobec tego pole powierzchni całkowitej walca wynosi:

$P_c=2\pi \cdot {\left(\frac{3\sqrt{3}}{2}\right)}^2+2\pi \cdot \frac{3\sqrt{3}}{2}\cdot 3\sqrt{3}=\frac{27}{2}\pi +27\pi =\frac{81}{2}\pi$.

bryła obrotowa, która powstaje przez obrót prostokąta wokół prostej zawierającej jeden bok

miara przyporządkowująca danej figurze liczbę nieujemną, charakteryzująca jej rozmiar