Figury na rysunku tworzone są według pewnej reguły. Odkryj te regułę i narysuj według odkrytej reguły jeszcze kilka kolejnych figur.

	Figury
numer figury	$1$	$2$	$3$
figura	RwMHmAKIldJSR Ilustracja przedstawia kwadrat podzielony na 9 równych mniejszych kwadratów, czyli w sposób uporządkowany możemy powiedzieć, że mamy trzy wiersze i trzy kolumny składające się z trzech kwadratów każdy. Usunięto dwa mniejsze kwadraty - środkowy w pierwszym wierszu i ostatni w drugim wierszu.	R1Z87DISbXRd1 Ilustracja przedstawia figurę składającą się z dziesięciu małych kwadratów. Kwadraty te ustawione są następująco: od lewej mamy kolumnę składającą się z czterech kwadratów. Od ostatniego kwadratu na dole odchodzą w ukośnej linii trzy kolejne kwadraty oraz od tego samego kwadratu położonego najniżej z pierwszej kolumny odchodzą w linii poziomej trzy kolejne kwadraty.	R1aso5YlVSVPW Ilustracja przedstawia figurę składającą się z trzynastu małych kwadratów. Kwadraty te ustawione są następująco: od lewej mamy kolumnę składającą się z pięciu kwadratów. Od ostatniego kwadratu na dole odchodzą w ukośnej linii cztery kolejne kwadraty oraz od tego samego kwadratu położonego najniżej z pierwszej kolumny odchodzą w linii poziomej cztery kolejne kwadraty.
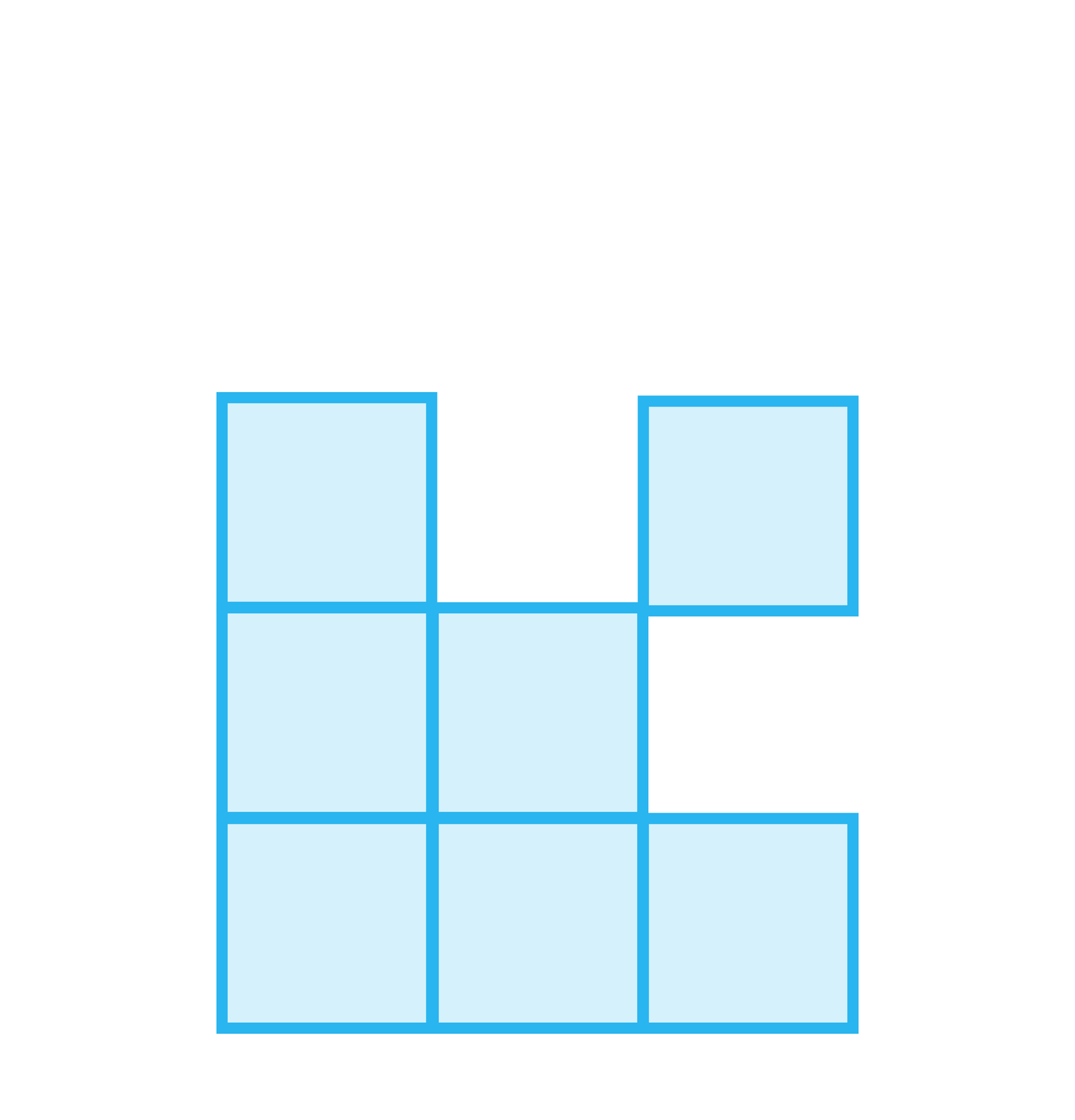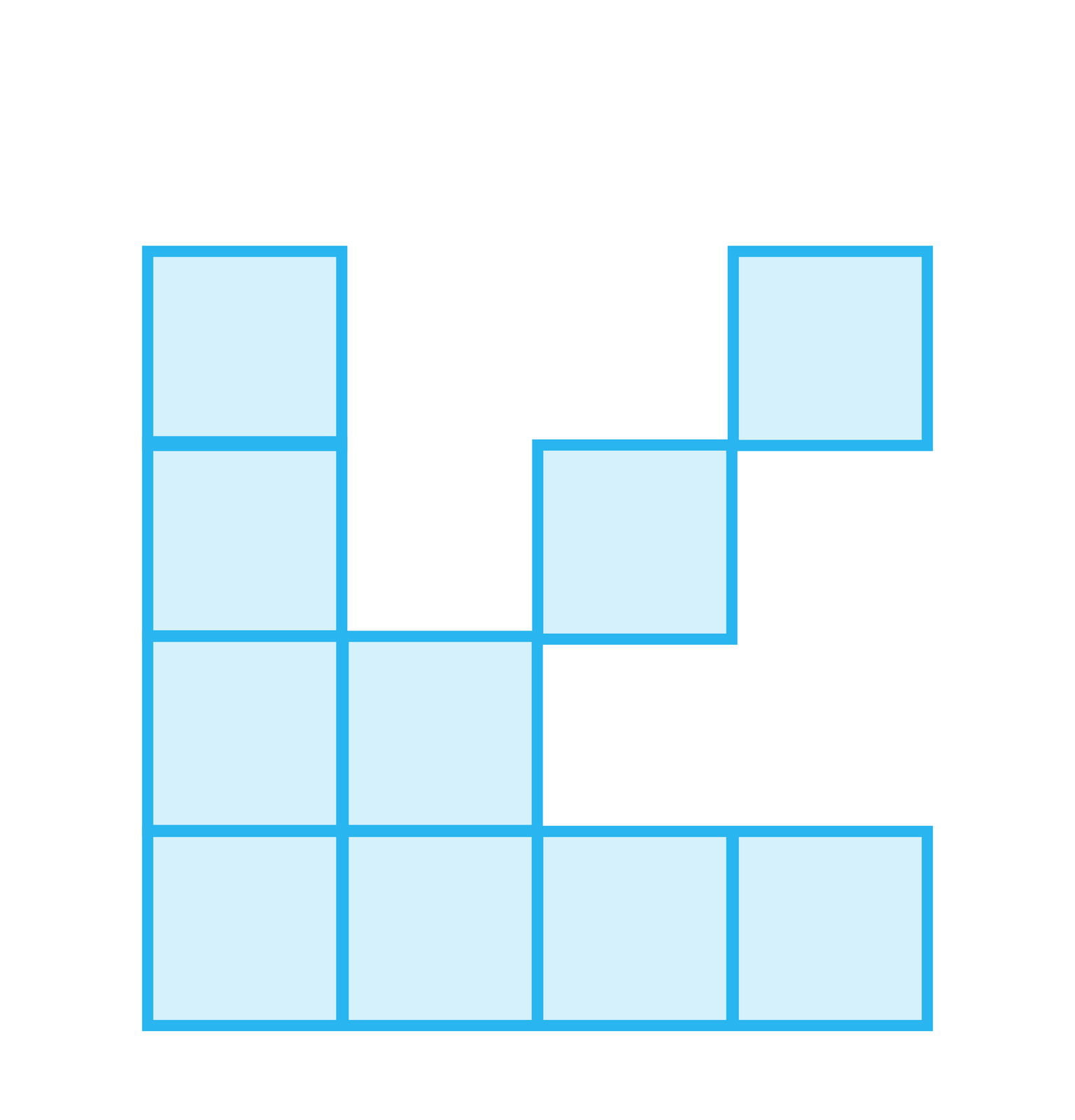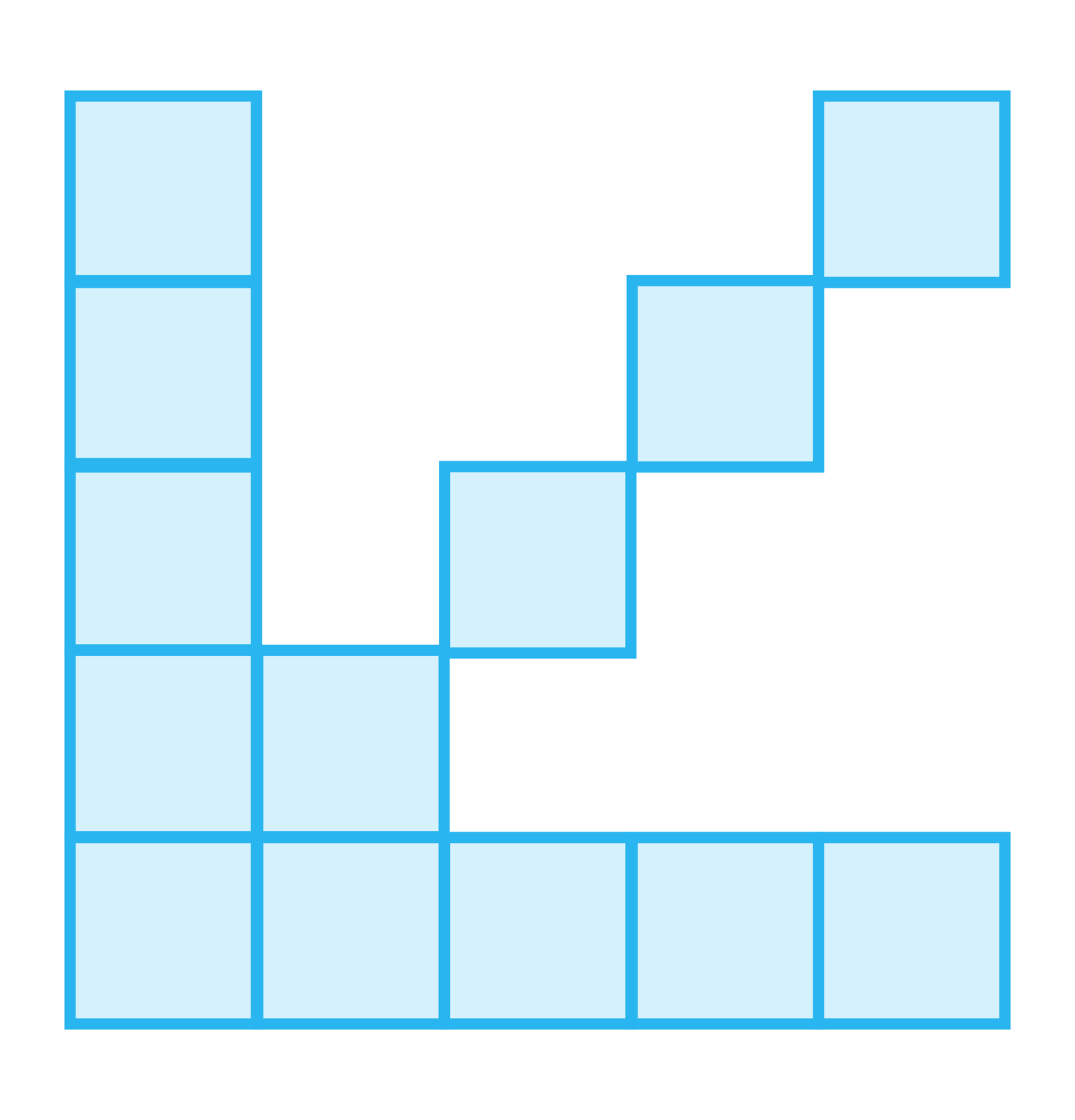liczba kwadratów, z których zbudowana jest figura	$7$	$10$	$13$

Kolejne figury $1$, $2$, $3$, $...$ składają się odpowiednio z $7$, $10$, $13$, $...$ kwadratów. Numerom figur wyrażonym przez kolejne liczby naturalne dodatnie przyporządkowane są liczby kwadratów, z których są zbudowane.

Możemy więc powiedzieć, że nadając figurom numery, ustawimy je w ciąg. Każdemu numerowi odpowiada jedna figura. Zatem utworzyliśmy w ten sposób pewną funkcję $f$ określoną na zbiorze liczb naturalnych dodatnich taką, że:

$f\left(1\right)=7$, $f\left(2\right)=10$, $f\left(3\right)=13$, $...$

Każdemu z pięciu laureatów konkursu matematycznego przypisujemy jego imię.

W ten sposób opisaliśmy funkcję określoną na podzbiorze zbioru liczb naturalnych: $\left\{1, 2, 3, 4, 5\right\}$.

Taki rodzaj funkcji to przkład  ciągu, a wartości funkcji  to  wyrazy ciągu.

Wyrazy ciągu to w tym przypadku: Aleksandra, Szymon, Wojciech, Natalia, Grażyna.

W tabelce przedstawiono prognozowane szanse opadów w miejscowości Kalino w dniach 1 – 6 października.

Tabelka opisuje funkcję $p$ określoną na podzbiorze zbioru liczb naturalnych: $\left\{1, 2, 3, 4, 5, 6\right\}$. Wiemy już, że jest to pewien ciąg.

Przyjmijmy za wyrazy ciągu, liczby określające poszczególne procenty ( dla np. 63%  przyjmijmy 63).  Zatem wyrazy ciągu to w tym przypadku:

$p\left(1\right)=63$

$p\left(2\right)=17$

$p\left(3\right)=21$

$p\left(4\right)=30$

$p\left(5\right)=9$

$p\left(6\right)=42$

Dla ciągów przyjęto trochę inne oznaczenia niż dla funkcji.

Zatem

$p\left(1\right)$ oznaczamy $p_1$ i zapisujemy $p_1=63$

$p\left(2\right)$ oznaczamy $p_2$ i zapisujemy $p_2=17$

$p\left(3\right)$ oznaczamy $p_3$ i zapisujemy $p_3=21$

$p\left(4\right)$ oznaczamy $p_4$ i zapisujemy $p_4=30$

$p\left(5\right)$ oznaczamy $p_5$ i zapisujemy $p_5=9$

$p\left(6\right)$ oznaczamy $p_6$ i zapisujemy $p_6=42$

Utworzony ciąg oznaczamy: $\left(p_n\right)$.

Zapisujemy:

$\left(p_n\right)=\left(63, 17, 21, 30, 9, 42\right)$.

Ciągiem nieskończonym nazywamy funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich.

Ciągiem skończonym nazywamy funkcję, której dziedziną jest zbiór $n$ liczb naturalnych $\left\{1, 2, 3, ..., n\right\}$.

Przyporządkowujemy każdej liczbie naturalnej dodatniej jej odwrotność.

Liczbie $1$ przyporządkowujemy $1$.

Liczbie $2$ przyporządkowujemy $\frac{1}{2}$.

Liczbie $3$ przyporządkowujemy $\frac{1}{3}$.

Liczbie $4$ przyporządkowujemy $\frac{1}{4}$.

$...$

$...$

Zbudowany w ten sposób ciąg ma postać:

$\left(1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, ...,\frac{1}{n}, ...\right)$

Pierwszy wyraz tego ciągu to $1$, a $n$–ty wyraz to $\frac{1}{n}$.

Jest to przykład ciągu nieskończonegociąg nieskończonyciągu nieskończonego. Taki ciąg ma pierwszy wyraz, ale nie ma wyrazu ostatniego.

Tworzymy ciąg $\left(a_n\right)$, którego wyrazami są liczby przeciwne do kolejnych liczb naturalnych dodatnich parzystych mniejszych od $12$.

$\left(a_n\right)=\left(-2, -4, -6, -8, -10\right)$

Jest to przykład ciągu skończonego, pięciowyrazowego.

W ciągu istotne są nie tylko jego wyrazy, ale też ich kolejność. Ciąg skończonyciąg skończonyCiąg skończony ma pierwszy wyraz (w tym przypadku jest to $\left(-2\right)$) i ostatni wyraz (w tym przypadku jest to $\left(-10\right)$).

ciągiem nieskończonym nazywamy funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich

ciągiem skończonym nazywamy funkcję, której dziedziną jest zbiór $n$ liczb naturalnych $\left\{1, 2, 3, ..., n\right\}$