RIcNQOafvYPKX

Grafika przedstawia trójkąt prostokątny o przyprostokątnych $a$ oraz $b$ i przeciwprostokątną $c$.

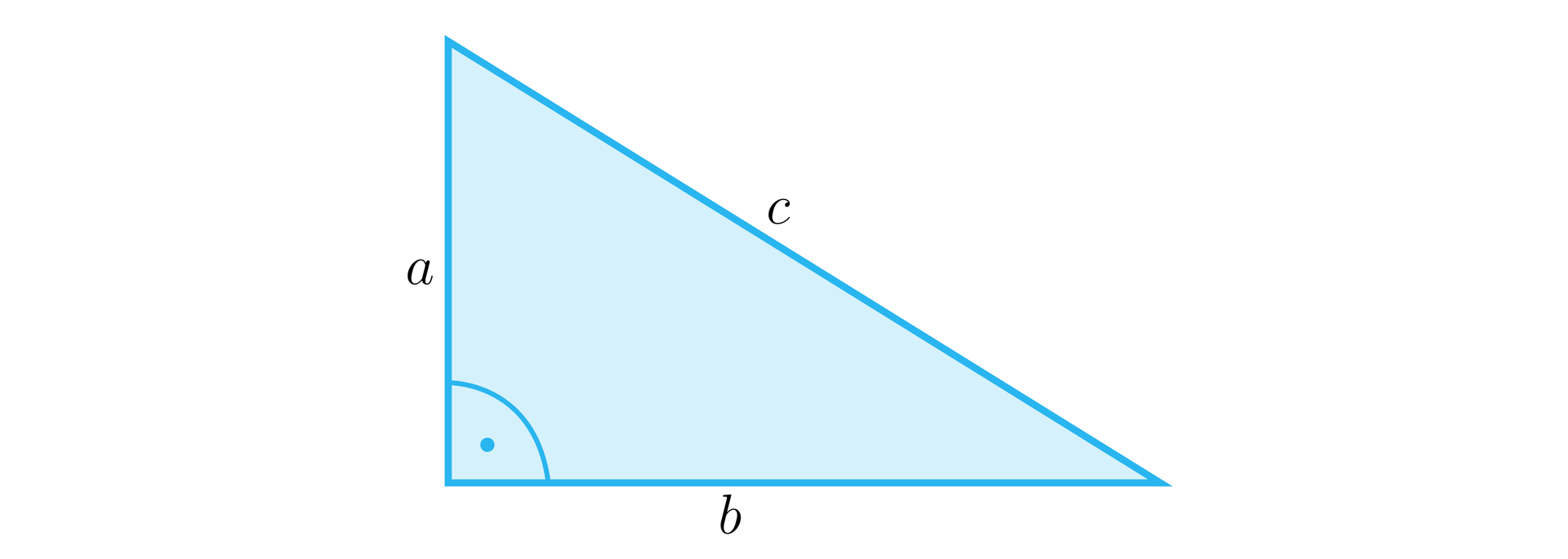
Na podstawie twierdzenia Pitagorasa dla trójkąta przedstawionego na  powyższym rysunku, możemy zapisać równanie $a^2+b^2=c^2$.

W równaniu tym pojawiają się trzy niewiadome $a$, $b$ i $c$.

W matematyce możemy również spotkać się z równaniami, w których występują dwie niewiadome. Poniżej przykłady takich równań.

$x+y=4$

$\frac{1}{2x}+\frac{1}{y}=5$

$x^2+3y^2=12$

$y=x^3-5x^2+5x-1$

Wzory funkcji zapisujemy często  w postaci równania z dwiema niewiadomymirównanie z dwiema lub trzema niewiadomymirównania z dwiema niewiadomymi.

$y=x$

$y=2x+5$

$y=\left|x\right|-2$

$y=\sqrt{x}$

RlDrDb14dLPkn

Grafika przedstawia wagę szalkową. Na lewej szalce stoją dwie butelki soku i odważnik o masie $1\mathrm{kg}$. Na prawej szalce leży arbuz oraz dwa odważniki, o masie $2\mathrm{kg}$ każdy. Szalki są w równowadze.

Przymnijmy, że $x$ – to masa soku, a $y$ – to masa arbuza.

Wtedy sytuację przedstawioną na rysunku możemy zapisać w postaci równania $2x+1=4+y$.

Takie równanie nazywamy równaniem pierwszego stopnia z dwiema niewiadomymirównanie pierwszego stopnia z dwiema niewiadomymirównaniem pierwszego stopnia z dwiema niewiadomymi.

Równanie, w którym występują dwie niewiadome i obie występują w pierwszej potędze, nazywamy równaniem pierwszego stopnia z dwiema niewiadomymi.

Równanie z niewiadomymi  $x$ i $y$ przyjmuje postać

gdzie:
$a, b, c\in \mathrm{ℝ}$ i $a^2+b^2\ne 0$.

Za pomocą równania z dwiema niewiadomymi możemy opisywać sytuacje przedstawione w zadaniach tekstowych.

a) Motorówka płynie z prądem rzeki z prędkością $20 \frac{\mathrm{km}}{\mathrm{h}}$. Zapisz odpowiednie równanie.

Wprowadzamy oznaczenia:
$x$ – prędkość prądu rzeki,
$y$ – prędkość własna motorówki.

Zapisujemy równanie.

$x+y=20$

b) Tomek ma w skarbonce $71 \mathrm{zł}$ w monetach $5 \mathrm{zł}$ i $2 \mathrm{zł}$. Zapisz odpowiednie równanie.

Wprowadzamy oznaczenia:
$x$ – liczba monet $2 \mathrm{zł}$,
$y$ – liczba monet $5 \mathrm{zł}$.

Zapisujemy równanie.

$2x+5y=71$

c) Za $3 \mathrm{kg}$ jabłek i $1,5 \mathrm{kg}$ czereśni zapłacono $15 \mathrm{zł}$. Zapisz odpowiednie równanie.

Wprowadzamy oznaczenia:
$x$ – cena $1 \mathrm{kg}$ jabłek,
$y$ – cena $1 \mathrm{kg}$ czereśni.

Zapisujemy równanie.

$3x+1,5y=15$

równanie, w którym występują dwie lub trzy niewiadome

równanie, w którym występują dwie niewiadome i obie występują w pierwszej potędze