Przeczytaj
Ciąg można określić między innymi poprzez podanie wzoru ogólnego. Można też podać jego pierwszy wyraz (lub kilku początkowych wyrazów) i regułę wyznaczania kolejnych wyrazów, w zależności od poprzednich, czyli określając definicję rekurencyjną ciągudefinicję rekurencyjną ciągu.
Mówimy, że ciąg jest zdefiniowany rekurencyjnie, jeżeli:
określony jest pewien skończony zbiór wyrazów tego ciągu (zwykle jest to pierwszy wyraz ciągu lub kilka jego pierwszych wyrazów),
pozostałe wyrazy ciągu są wyrażone za pomocą poprzednich wyrazów tego ciągu.
Znając określenie rekurencyjne ciągu, jest na ogół trudno znaleźć wzór ogólny ciągu. Znacznie łatwiej jest natomiast zapisać ciąg w sposób rekurencyjny, mając wzór ogólny ciągu.
Ciąg dla określony jest wzorem ogólnym . Określimy ten ciąg rekurencyjnie.
Rozwiązanie
Zapisujemy najpierw wzór ciągu w prostszej postaci.
Teraz obliczamy wartość pierwszego wyrazu ciągu.
Wyznaczamy wyraz .
Przekształcamy tak wyrażenie, aby wyraz zapisać w zależności od wyrazu .
Zapisujemy wzór rekurencyjny ciągu.
W historii matematyki ważną rolę odgrywa ciąg liczbowy , zwany ciągiem Jacobsthal – Lucasa, nazwany tak na cześć dwóch znamienitych dziewiętnastowiecznych matematyków – Niemca Ernsta Jacobsthala i Francuza Eduarda Lucasa.
Początkowe wyrazy tego ciągu to:
, , , , , , , , , , , , , , , , , , , , ,……
Wzór ogólny ciągu: dla .
Znajdziemy wzór rekurencyjny tego ciągu.
Rozwiązanie
Znajdujemy pierwszy wyraz ciągu, czyli w tym przypadku wyraz , oraz drugi wyraz ciągu, czyli .
Wyznaczamy wyraz .
Przekształcamy tak wyrażenie, aby wyraz zapisać w zależności od wyrazu .
Zapisujemy wzór rekurencyjny ciągu.
Teraz trudniejszy przykład, wymagający nieco zastanowienia.
Ciąg określony jest dla wzorem ogólnym . Podamy przykład wzoru rekurencyjnego tego ciągu.
Rozwiązanie
Wyznaczamy pierwszy wyraz tego ciągu.
Zapisujemy wyraz .
Przekształcamy tak wyrażenie, aby wyraz zapisać w zależności od wyrazu .
Zapisujemy wzór rekurencyjny ciągu.
Na rysunku przedstawiono wykres skończonego ciągu . Opiszemy ten ciąg wzorem rekurencyjnym.
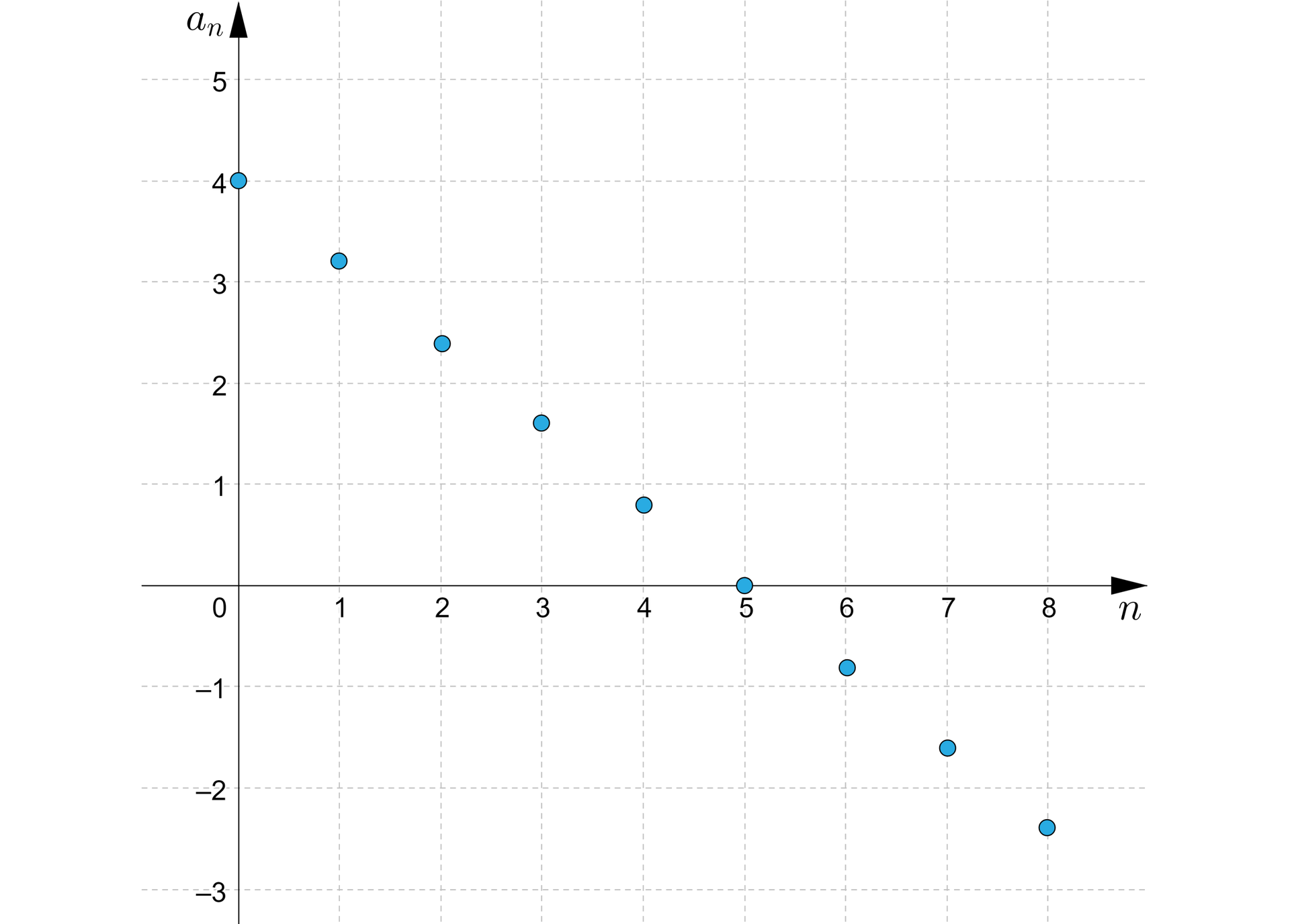
Rozwiązanie
Zauważmy, że wyrazy ciągu leżą na prostej.

Wyznaczymy najpierw równanie tej prostej.
Zapisujemy równanie prostej w postaci kierunkowej.
, gdzie , to współczynniki liczbowe.
Odczytujemy z wykresu współrzędne dwóch punktów należących do tej prostej, np. i i podstawiamy do równania prostej.
i .
Stąd
i , czyli .
Wzór ogólny ciągu:
, gdzie .
Teraz możemy przystąpić do wyznaczania wzoru rekurencyjnego. Odczytujemy z wykresu wyraz .
Obliczamy wyraz .
Obliczamy i przekształcamy.
Wzór rekurencyjny:
Podobnie jak wzór ogólny ciągu, wzór rekurencyjny można wyznaczać różnymi sposobami. W zależności od użytego sposobu, ten sam ciąg można opisać różnymi wzorami rekurencyjnymi.
Określimy dwoma sposobami wzór rekurencyjny ciągu opisanego słownie:
każdej liczbie naturalnej dodatniej przyporządkowany jest jej kwadrat.
Rozwiązanie
Wzór na -ty wyraz ciągu: .
Wyznaczamy wyraz pierwszy: oraz wyraz .
.
Ciąg określimy rekurencyjnie na podstawie różnicy:
.
Otrzymujemy wzór rekurencyjny.
Wzór rekurencyjny można też uzyskać na podstawie ilorazu.
Teraz otrzymujemy nieco inny wzór rekurencyjny.
Słownik
mówimy, że ciąg jest zdefiniowany rekurencyjnie, jeżeli:
określony jest pewien skończony zbiór wyrazów tego ciągu (zwykle jest to pierwszy wyraz ciągu lub kilka jego pierwszych wyrazów),
pozostałe wyrazy ciągu są wyrażone za pomocą poprzednich wyrazów tego ciągu