Przeczytaj

Okrąg na płaszczyźnie kartezjańskiej opisujemy za pomocą równania. Wyróżniamy dwie postacie tego równania:

równanie okręgu w postaci ogólnej $x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ , gdzie promień okręgu obliczamy ze wzoru $r = \sqrt{a^{2} + b^{2} - c}$ , zaś punkt $S = (a, b)$ jest środkiem okręgu,
równanie okręgu w postaci kanonicznej ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ , gdzie $r$ nazywamy promieniem okręgu, zaś punkt $S = (a, b)$ środkiem okręgu.

Wzajemne położenie dwóch okręgów na płaszczyźnie kartezjańskiej

Załóżmy, że mamy dane dwa okręgi na płaszczyźnie kartezjańskiej. Wprowadźmy oznaczenia:

$S_{1}, S_{2}$ - środki okręgów,

$r_{1}, r_{2}$ - promienie okręgów.

1. Okręgi styczne wewnętrznie lub zewnętrznie.

Okręgi są styczne wewnętrznie, gdy odległość między ich środkami jest równa wartości bezwzględnej różnicy ich promieni:

$|S_{1} S_{2}| = |r_{2} - r_{1}|$ .

Na rysunku przedstawiono okręgi styczne wewnętrznie o równaniach:

${(x - 3)}^{2} + {(y - 4)}^{2} = 9$ oraz ${(x - \frac{3}{2})}^{2} + {(y - 4)}^{2} = \frac{9}{4}$ , skąd otrzymujemy:

$S_{1} = (3, 4)$ oraz $r_{1} = 3$ ,

$S_{2} = (\frac{3}{2}, 4)$ oraz $r_{2} = \frac{3}{2}$ .

R1CB705DHAm9s

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do sześciu oraz z pionową osią Y od minus jeden do siedmiu. W pierwszej ćwiartce układu narysowano dwa okręgi. Duży okrąg ma środek w punkcie S1=3;4 i promień r1. Mniejszy okrąg jest narysowany wewnątrz dużego. Ma on środek w punkcie S2=32;4 oraz promień r2. Okręgi te są styczne wewnętrznie w punkcie o współrzędnych 0;4.

Okręgi są styczne zewnętrznie, gdy odległość między ich środkami jest równa sumie ich promieni:

$| S_{1} S_{2} | = r_{1} + r_{2}$ .

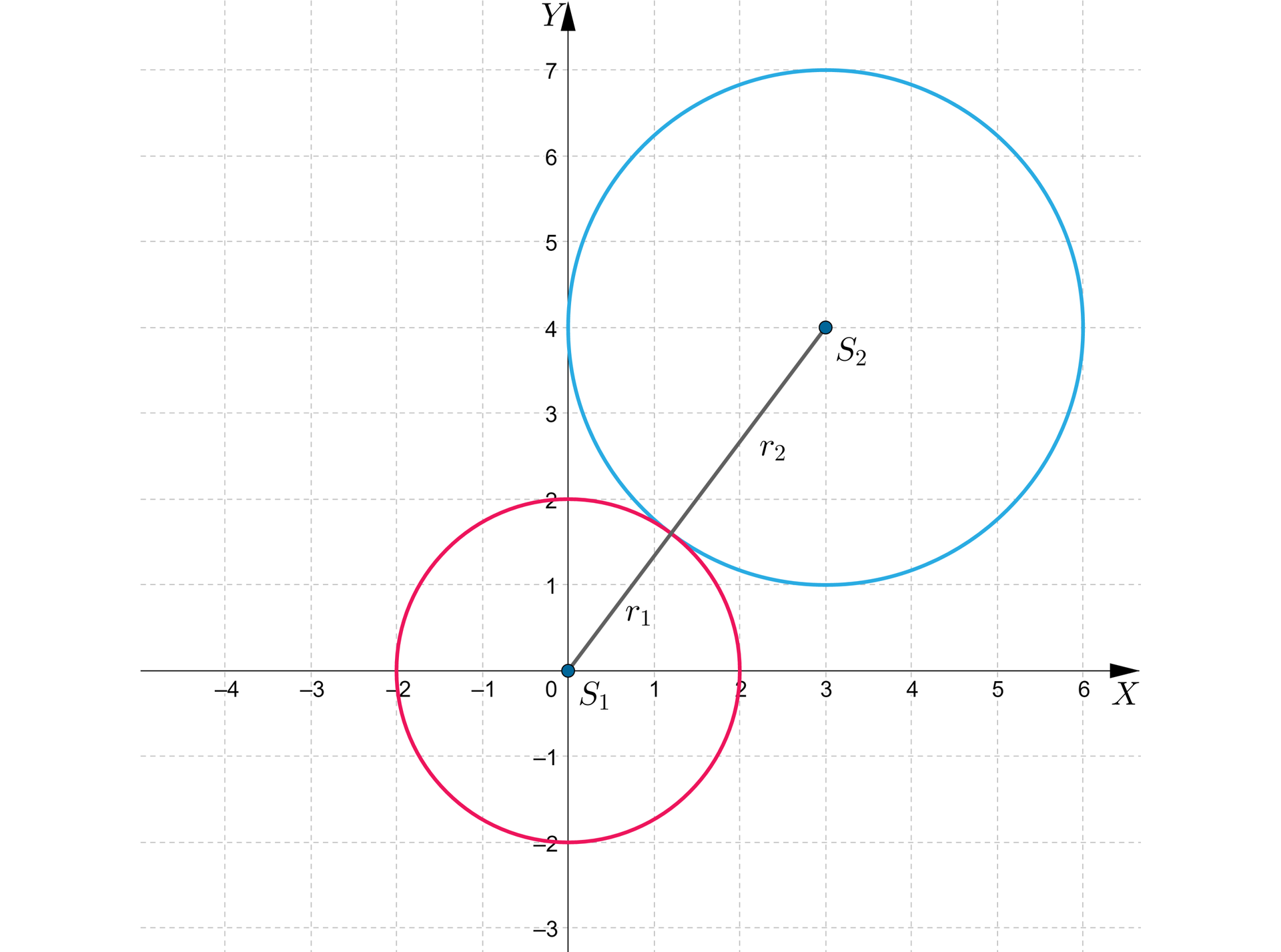
Na rysunku przedstawiono okręgi styczne zewnętrznie o równaniach:

${(x - 3)}^{2} + {(y - 4)}^{2} = 9$ oraz $x^{2} + y^{2} = 4$ , skąd otrzymujemy

$S_{1} = (0, 0)$ oraz $r_{1} = 2$ ,

$S_{2} = (3, 4)$ oraz $r_{2} = 3$ ,

Rd4gztTZLFW5J

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do sześciu oraz z pionową osią Y od minus trzech do siedmiu. Na płaszczyźnie narysowano dwa okręgi. Duży okrąg znajduje się w pierwszej ćwiartce. Jego środek ma współrzędne S2=3;4, a jego promień wynosi r2. Mniejszy okrąg przechodzi przez wszystkie ćwiartki układu, bowiem jego środek znajduje się w początku układu współrzędnych, czyli S1=0;0, a jego promień to r1. Okręgi te są styczne zewnętrznie w punkcie leżącym w pierwszej ćwiartce układu. Promienie okręgów narysowano w taki sposób, że wspólnie tworzą one odcinek S1S2.

2. Okręgi rozłączne wewnętrznie lub zewnętrznie.

Okręgi są rozłączne wewnętrznie, gdy odległość pomiędzy ich środkami jest mniejsza niż wartość bezwzględna różnicy ich promieni:

$| S_{1} S_{2} | < | r_{2} - r_{1} |$ .

Na rysunku przedstawiono okręgi rozłączne wewnętrznie o równaniach:

${(x - 3)}^{2} + {(y - 4)}^{2} = 9$ oraz ${(x - 2)}^{2} + {(y - 4)}^{2} = 2$ , skąd otrzymujemy

$S_{1} = (3, 4)$ oraz $r_{1} = 3$ ,

$S_{2} = (2, 4)$ oraz $r_{2} = \sqrt{2}$ .

R16t8UVkfMfXQ

Okręgi są rozłączne zewnętrznie, gdy odległość między ich środkami jest większa niż suma ich promieni:

$|S_{1} S_{2}| > r_{1} + r_{2}$

Na rysunku przedstawiono okręgi rozłączne zewnętrznie o równaniach:

$x^{2} + y^{2} = 4$ oraz ${(x - 3)}^{2} + {(y - 4)}^{2} = 2$ , skąd otrzymujemy

$S_{1} = (0, 0)$ oraz $r_{1} = 2$ ,

$S_{2} = (3, 4)$ oraz $r_{2} = \sqrt{2}$ .

RgS16A3yMtXfQ

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do sześciu oraz z pionową osią Y od minus trzech do sześciu. Na płaszczyźnie narysowano dwa okręgi. Mniejszy okrąg znajduje się w pierwszej ćwiartce. Jego środek ma współrzędne S2=3;4, a jego promień wynosi r2. Większy okrąg przechodzi przez wszystkie ćwiartki układu, bowiem jego środek znajduje się w początku układu współrzędnych, czyli S1=0;0, a jego promień to r1. Okręgi te są rozłączne zewnętrznie, czyli nie mają żadnych punktów wspólnych.

3. Okręgi przecinające się.

Okręgi przecinają się w dwóch punktach, gdy odległość między środkami okręgów jest większa od wartości bezwzględnej różnicy ich promieni i mniejsza od sumy ich promieni:

$|r_{1} - r_{2}| < |S_{1} S_{2}| < r_{1} + r_{2}$

Na rysunku przedstawiono okręgi przecinające się o równaniach:

${(x - 3)}^{2} + y^{2} = 4$ oraz $x^{2} + y^{2} = 9$ , skąd otrzymujemy

$S_{1} = (0, 0)$ oraz $r_{1} = 3$ ,

$S_{2} = (3, 0)$ oraz $r_{2} = 2$ .

RvKyGcItt1axh

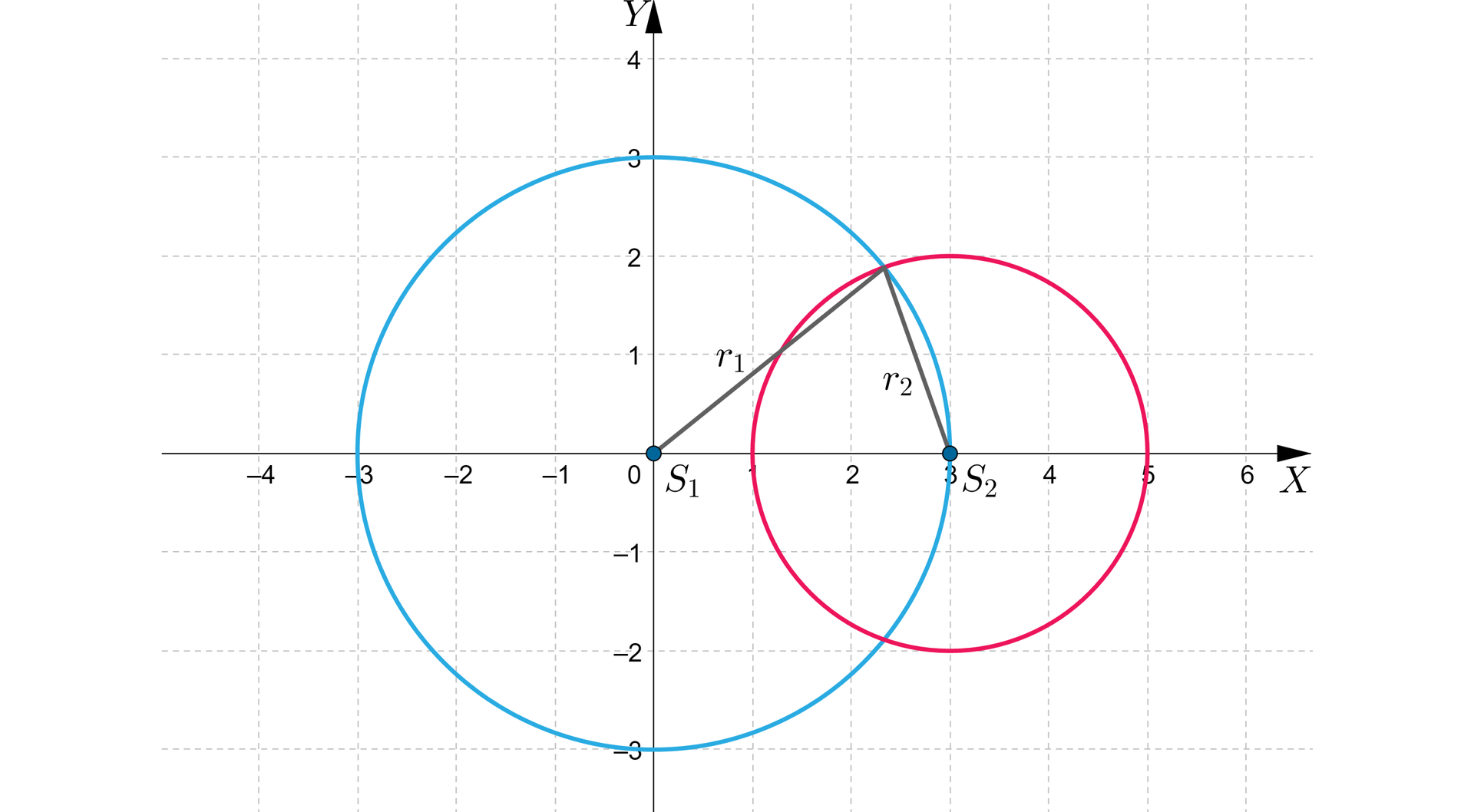
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do sześciu oraz z pionową osią Y od minus czterech do czterech. Na płaszczyźnie narysowano dwa okręgi. Mniejszy okrąg znajduje się w pierwszej i w czwartej ćwiartce. Jego środek ma współrzędne S2=0;3, a jego promień wynosi r2. Większy okrąg przechodzi przez wszystkie ćwiartki układu, bowiem jego środek znajduje się w początku układu współrzędnych, czyli S1=0;0, a jego promień to r1. Okręgi te przecinają się, co oznacza, że mają dwa punkty wspólne. Promienie okręgów narysowano w taki sposób, że przebiegają od środków swoich okręgów do jednego z punktów wspólnych, który znajduje się w pierwszej ćwiartce. Drugi punkt wspólny znajduje się w czwartej ćwiartce.

Z opisanych wyżej możliwości wzajemnego położenia dwóch okręgów na płaszczyźnie kartezjańskiej wynika pewna własność.

Liczba punktów wspólnych dwóch okręgów.

Własność: Liczba punktów wspólnych dwóch okręgów.

Dwa okręgi na płaszczyźnie kartezjańskiej mają:

$0$ punktów wspólnych, gdy są rozłączne wewnętrznie lub zewnętrznie,
$1$ punkt wspólny, gdy są styczne wewnętrznie lub zewnętrznie,
$2$ punkty wspólne, gdy się przecinają,
nieskończenie wiele punktów wspólnych, gdy się pokrywają.

Ciekawostka

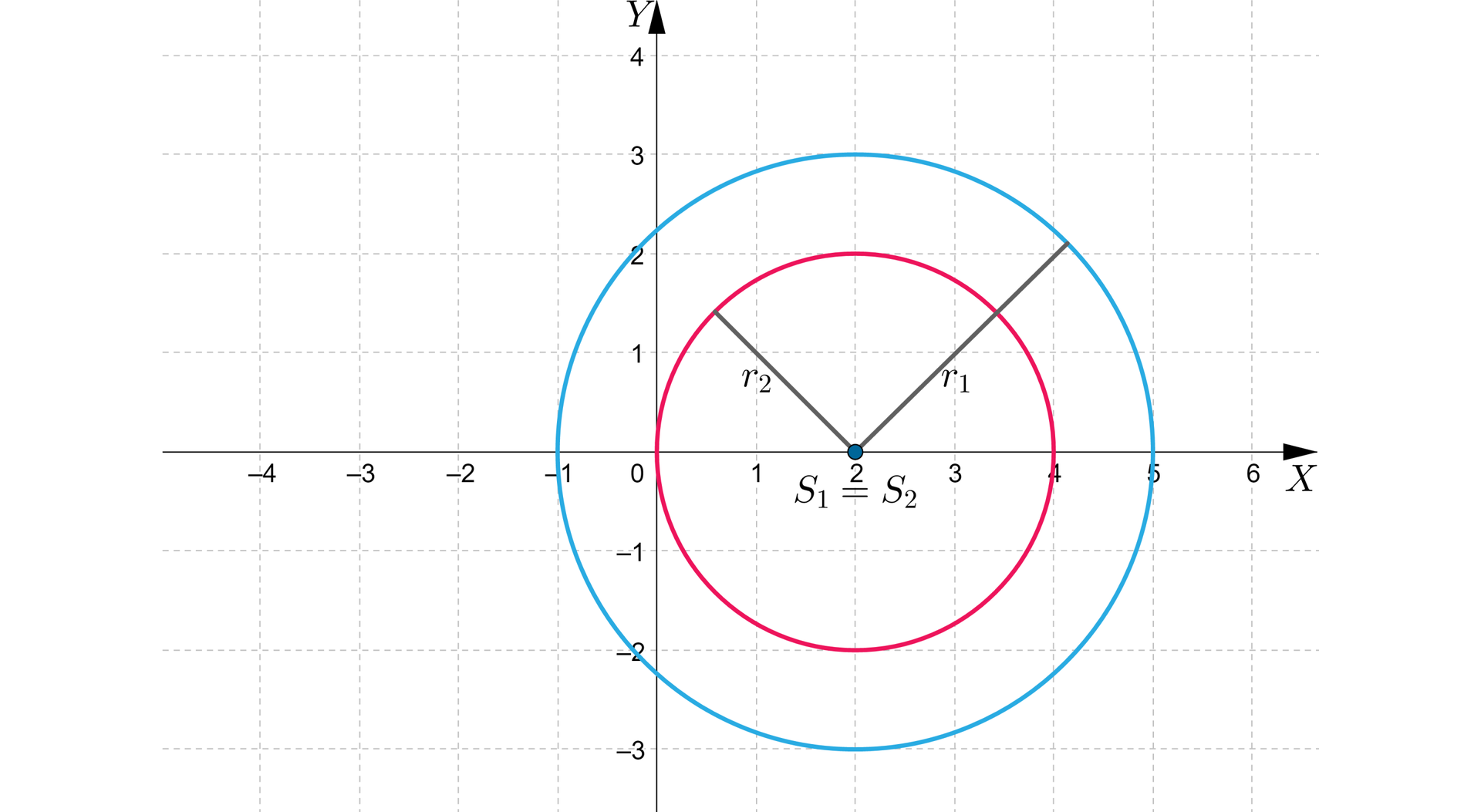
Okręgi o wspólnym środku nazywamy okręgami współśrodkowymi. Zaliczamy je do grupy okręgów rozłącznych.

Na rysunku przedstawiono okręgi o równaniach:

${(x - 2)}^{2} + y^{2} = 9$ oraz ${(x - 2)}^{2} + y^{2} = 4$ , skąd otrzymujemy

$S_{1} = S_{2} = (2, 0)$ , $r_{1} = 2$ i $r_{2} = 3$ .

RMO2rPUd2Kx62

Do analizy wzajemnego położenia okręgów na płaszczyźnie kartezjańskiej wykorzystamy wzór na odległość dwóch punktów o współrzędnych $A = (x_{1}, y_{1})$ i $B = (x_{2}, y_{2})$ .

Wówczas: $|A B| = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ .

Przykład 1

Zbadamy wzajemne położenie okręgów zadanych równaniami w postaci kanonicznejrównaniami w postaci kanonicznej: ${(x + 2)}^{2} + y^{2} = 4$ i ${(x + 1)}^{2} + {(y - 4)}^{2} = 5$ .

Rozwiązanie:

Ustalmy środki i promienie okręgów. Mamy:

$S_{1} = (- 2, 0)$ oraz $r_{1} = 2$ ,

$S_{2} = (- 1, 4)$ oraz $r_{2} = \sqrt{5}$ .

Obliczmy odległość pomiędzy środkami tych okręgów:

$|S_{1} S_{2}| = \sqrt{{(- 1 + 2)}^{2} + {(4 - 0)}^{2}} = \sqrt{17}$ .

Wyznaczmy sumę oraz różnicę promieni:

$r_{1} + r_{2} = 2 + \sqrt{5}$ oraz $r_{2} - r_{1} = \sqrt{5} - 2$ .

Ponieważ zachodzi warunek $| r_{2} - r_{1} | < | S_{1} S_{2} | < r_{1} + r_{2}$ , zatem okręgi przecinają się w dwóch punktach.

Przykład 2

Zbadamy wzajemne położenie okręgów zadanych równaniami: $x^{2} - 2 x + y^{2} + 2 y - 2 = 0$ oraz $x^{2} + 4 x + y^{2} - 4 y + 7 = 0$ .

Rozwiązanie:

Równanie pierwszego okręgu możemy zapisać w postaci ${(x - 1)}^{2} + {(y + 1)}^{2} = 4$ , a drugiego okręgu w postaci ${(x + 2)}^{2} + {(y - 2)}^{2} = 1$ .

Środki i promienie tych okręgów wynoszą odpowiednio:

$S_{1} = (1, - 1)$ oraz $r_{1} = 2$ ,

$S_{2} = (- 2, 2)$ oraz $r_{2} = 1$ .

Obliczmy odległość pomiedzy środkami tych okręgów:

$|S_{1} S_{2}| = \sqrt{{(- 2 - 1)}^{2} + {(2 + 1)}^{2}} = 3 \sqrt{2}$ .

Zauważmy, że $r_{1} + r_{2} = 2 + 1 = 3$ .

Ponieważ zachodzi warunek $| S_{1} S_{2} | > r_{1} + r_{2}$ , zatem okręgi są rozłączne zewnętrznie.

Jeżeli mamy dane równanie okręgu w postaci ogólnejrównanie okręgu w postaci ogólnejrównanie okręgu w postaci ogólnej, wówczas możemy wyznaczyć jego środek i promień, korzystając ze wzorów.

Przykład 3

Zbadamy wzajemne położenie okręgów zadanych równaniami: $x^{2} + {(y + 1)}^{2} = 4$ oraz $x^{2} + 4 x + y^{2} - 2 y - 20 = 0$ .

Rozwiązanie:

Środek oraz promień pierwszego okręgu wynoszą:

$S_{1} = (0, - 1)$ i $r_{1} = 2$ .

Do wyznaczenia środka i promienia drugiego okręgu wykorzystamy wzór na równanie okręgu w postaci ogólnej $x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ oraz wzór na promień $r = \sqrt{a^{2} + b^{2} - c}$ .

Otrzymujemy:

$- 2 a = 4$ oraz $- 2 b = - 2$ , co daje $a = - 2$ i $b = 1$

Środek okręgu ma zatem współrzędne $S_{2} = (- 2, 1)$ .

Promień okręgu obliczymy po podstawieniu do wzoru:

$r_{2} = \sqrt{{(- 2)}^{2} + 1^{2} + 20} = \sqrt{25} = 5$

Obliczmy odległość pomiędzy środkami tych okręgów:

$|S_{1} S_{2}| = \sqrt{{(- 2 - 0)}^{2} + {(1 + 1)}^{2}} = 2 \sqrt{2}$

Zauważmy, że $|r_{2} - r_{1}| = 5 - 2 = 3$ .

Ponieważ $|S_{1} S_{2}| < |r_{2} - r_{1}|$ , zatem okręgi są rozłączne wewnętrznie.

Mając dane równanie okręgu z parametrem, możemy wyznaczyć jego wartość, jeżeli wiemy, czy okręgi są styczne, przecinające się lub rozłączne.

Przykład 4

Wyznaczymy, dla jakiej wartości parametru $m$ okręgi o równaniach ${(x - 2)}^{2} + y^{2} = 9$ i $x^{2} + {(y - 2 \sqrt{3})}^{2} = m^{2} - 1$ są styczne zewnętrznie.

Z podanych równań możemy odczytać środki oraz promienie okręgów.

Zatem:

$S_{1} = (2, 0)$ oraz $r_{1} = 3$

$S_{2} = (0, 2 \sqrt{3})$ oraz $r_{2} = \sqrt{m^{2} - 1}$ .

Z warunku, że promień okręgu jest zawsze większy od $0$ otrzymujemy nierówność:

$m^{2} - 1 > 0$ , zatem $m \in (- \infty, - 1) \cup (1, \infty)$ .

Jeżeli okręgi są styczne zewnętrznie, to prawdziwy jest warunek:

$|S_{1} S_{2}| = r_{1} + r_{2}$

Obliczmy odległość pomiędzy środkami tych okręgów:

$|S_{1} S_{2}| = \sqrt{{(0 - 2)}^{2} + {(2 \sqrt{3} - 0)}^{2}} = 4$

Do wyznaczenia wartości parametru $m$ rozwiązujemy równanie:

$4 = \sqrt{m^{2} - 1} + 3$ , czyli $m^{2} = 2$ .

Rozwiązaniami równania są liczby $\sqrt{2}$ lub $- \sqrt{2}$ .

Okręgi są styczne zewnętrznie, gdy $m = \sqrt{2}$ lub $m = - \sqrt{2}$ .

W celu wyznaczenia punktów wspólnych dwóch okręgów rozwiązujemy układ równań kwadratowych.

Przykład 5

Wyznaczymy punkty wspólne okręgów określonych równaniami ${(x - 1)}^{2} + y^{2} = 9$ oraz $x^{2} + {(y + 1)}^{2} = 5$ .

Rozwiązanie:

W celu wyznaczenia punktów wspólnych tych okręgów rozwiążemy układ równań:

$\{\begin{cases} {(x - 1)}^{2} + y^{2} = 9 \\ x^{2} + {(y + 1)}^{2} = 5 \end{cases}$

Układ ten jest równoważny układowi równań:

$\{\begin{cases} x^{2} - 2 x + 1 + y^{2} = 9 \\ x^{2} + y^{2} + 2 y + 1 = 5 \end{cases}$

Jeżeli równania odejmiemy stronami, to otrzymujemy równanie $2 x + 2 y = - 4$ , czyli $y = - x - 2$ .

Po podstawieniu tego wyrażenia do pierwszego równania otrzymujemy równanie $x^{2} - 2 x + 1 + {(- x - 2)}^{2} = 9$ , które przekształcamy do postaci $x^{2} + x - 2 = 0$ .

Rozwiązaniami tego równania są liczby $x_{1} = - 2$ lub $x_{2} = 1$ .

Zatem okręgi mają dwa punkty wspólne, których drugie współrzędne wynoszą odpowiednio $y_{1} = 0$ oraz $y_{2} = - 3$ .

Okręgi przecinają się w punktach o współrzędnych $(- 2, 0)$ oraz $(1, - 3)$ .

Słownik

równanie okręgu w postaci ogólnej

$x^{2} + y^{2} - 2 a x - 2 b y + c = 0$ , gdzie promień okręgu obliczamy ze wzoru $r = \sqrt{a^{2} + b^{2} - c}$ i $a, b, c \in R$ oraz $S = (a, b)$ - środek okręgu

równanie okręgu w postaci kanonicznej

${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ , gdzie $r$ - promień okręgu, $S = (a, b)$ - środek okręgu

Wprowadzenie

Aplet

Wzajemne położenie dwóch okręgów na płaszczyźnie kartezjańskiej

Słownik