Przeczytaj

COVID–19 to ostra choroba zakaźna układu oddechowego wywołana zakażeniem wirusem SARS‑CoV-2. Główną droga rozprzestrzeniania się wirusa SARS jest przenoszenie się z człowieka na człowieka w postaci kropelkowej.

Pewna osoba nie wiedziała, że jest zarażona wirusem SARS i rozmawiając z dwoma przyjaciółmi kichnęła (nie zakrywając ust), zaraziła te osoby. Załóżmy, że każda z tych osób nim dowiedziała się, że jest chora i następnego dnia również zaraziła dwie osoby. Zakładając, że ten model będzie się powtarzał i każda chora osoba zarazi dwie inne, możemy przebieg rozprzestrzeniania się wirusa zobrazować na wykresie.

R138vMwucFA3P

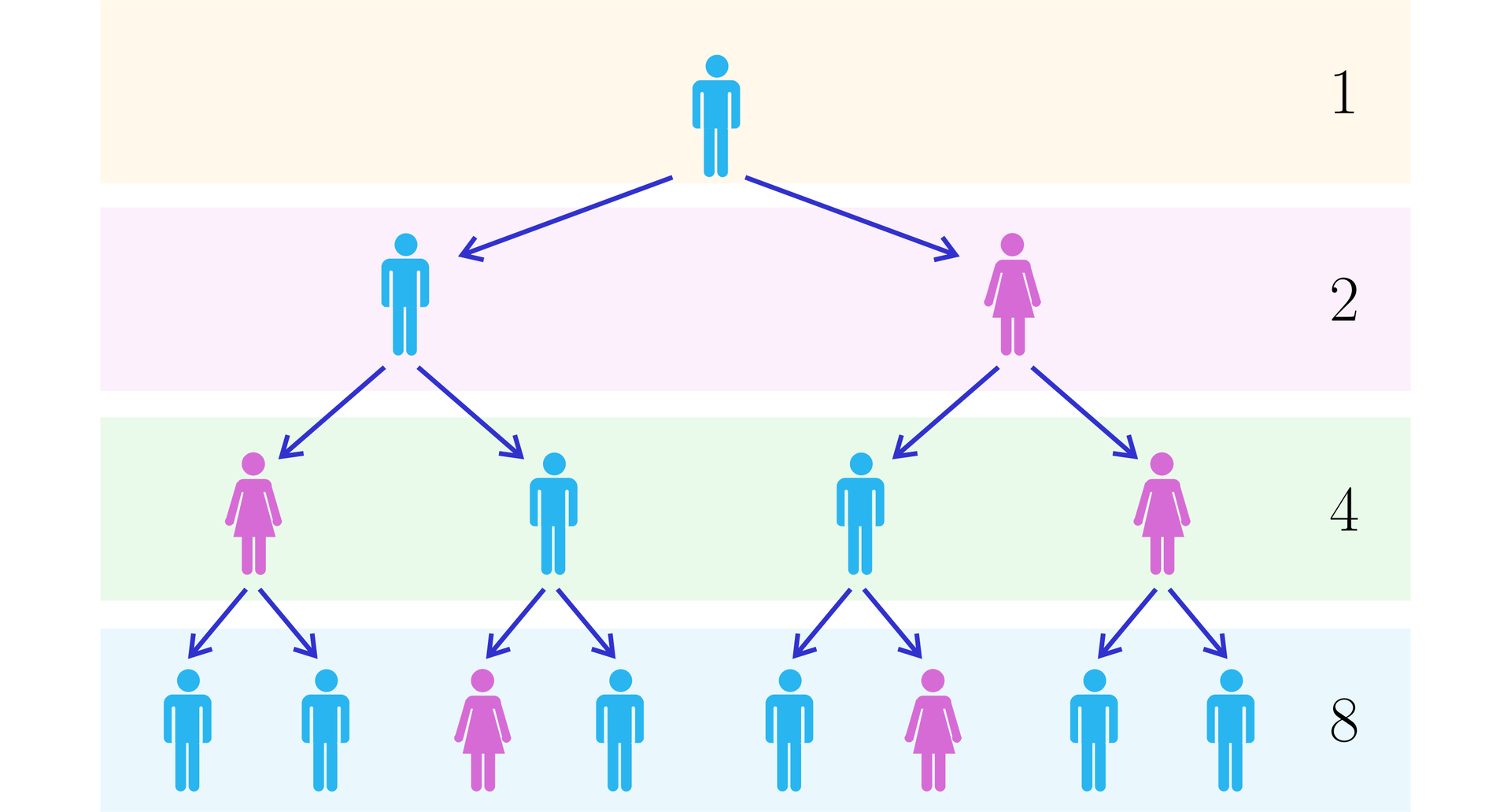
Schemat przedstawia drzewko zakażeń. Na szczycie jest jedna postać, od której mamy dwa rozgałęzienia do dwóch kolejnych postaci. Od każdej z nich mamy kolejne dwa i od tych postaci kolejne. Kolejne piętra drzewka są opisane liczbami zakażeń na danym poziomie, czyli: 1, 2, 4, 8

Liczby opisujące ilość zakażanych osób w kolejnych dniach możemy zapisać następująco:

1, 2, 4, 8, 16, . . .

Zauważ, że liczby te tworzą pewien ciąg, w którym kolejne wyrazy powstają z poprzednich poprzez pomnożenie przez $2$ . Jest to przykład ciągu (postępu) zwanego geometrycznym. Na podstawie powyższego schematu powiemy, że wirus SARS rozprzestrzenia się w postępie geometrycznym.

Zapiszmy teraz kilka kolejnych naturalnych potęg liczby $3$ .

3^{0}, 3^{1}, 3^{2}, 3^{3}, 3^{4}, 3^{5}, . . .

W tym przypadku kolejne wyrazy utworzonego ciągu (oprócz pierwszego) powstają poprzez pomnożenie wyrazu poprzedniego przez $3$ . Jest to również przykład ciągu geometrycznego.

Ciągi geometryczne mogą być ciągami nieskończonymi bądź skończonymi. Ale aby stwierdzić czy dany ciąg jest geometryczny, ten ciąg musi mieć co najmniej trzy wyrazy.

Ciąg geometryczny

Definicja: Ciąg geometryczny

Ciągiem geometrycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez pomnożenie wyrazu poprzedniego przez liczbę $q$ , zwaną ilorazem ciągu.

Przykład 1

Ciąg $(1, 5, 10)$ nie jest ciągiem geometrycznym, bo drugi wyraz powstaje z pierwszego poprzez pomnożenie przez $5$ , ale trzeci wyraz powstaje z drugiego poprzez pomnożenie przez $2$ .

Ciąg geometrycznyciąg geometrycznyCiąg geometryczny zwykle określany jest poprzez pierwszy wyraz ciągu i iloraz ciągu.

Przykład 2

Przykłady ciągów geometrycznych nieskończonych
Kolejne początkowe wyrazy ciągu	Pierwszy wyraz	Iloraz ciągu
$1, 2, 4, 8, 16, 32, 64, . . .$	$1$	$2$
$10, 50, 250, 1250, 6250, . . .$	$10$	$5$
$- 64, - 16, - 4, - 1, - \frac{1}{4}, - \frac{1}{16}, . . .$	$- 64$	$\frac{1}{4}$
$- 81, - 54, - 36, - 24, - 16, - \frac{32}{3}, . . .$	$- 81$	$\frac{2}{3}$
$\sqrt{2}, 2, 2 \sqrt{2}, 4, 4 \sqrt{2}, 8, 8 \sqrt{2}, . . .$	$\sqrt{2}$	$\sqrt{2}$
$0, 0, 0, 0, 0, 0, . . .$	$0$	Dowolna liczba rzeczywista

W powyższych przykładach ilorazem ciągu była liczba dodatnia (za wyjątkiem ciągu o wyrazach równych $0$ , którego ilorazem może być dowolna liczba rzeczywista). Ale iloraz może być też liczbą ujemną. Wówczas uzyskany ciąg (o wyrazach niezerowych), jest ciągiem naprzemiennym, to znaczy wystepują w nim na przemian wyrazy dodatnie i ujemne.

Przykład 3

Przykłady ciągów naprzemiennych skończonych
Kolejne początkowe wyrazy ciągu	Pierwszy wyraz	Iloraz ciągu
$1, - 1, 1, - 1, 1, - 1$	$1$	$- 1$
$- 5, 25, - 125, 625, - 3125$	$- 5$	$- 5$
$\frac{1}{3}, - \frac{1}{6}, \frac{1}{12}, - \frac{1}{24}, \frac{1}{48}$	$\frac{1}{3}$	$- \frac{1}{2}$

Ciekawym rodzajem ciągu geometrycznego jest ciąg stały. To znaczy taki, którego iloraz jest równy $1$ .

Przykład 4

Przykłady ciągów stałych
Kolejne początkowe wyrazy ciągu	Pierwszy wyraz	Iloraz ciągu
$- 1, - 1, - 1, - 1, - 1, - 1, . . .$	$- 1$	$1$
$5, 5, 5, 5, 5, . . .$	$5$	$1$
$\frac{1}{3}, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}, . . .$	$\frac{1}{3}$	$1$

Z określenia ciągu geometrycznego wynika, że iloraz uzyskany poprzez podzielenie wyrazu następnego przez poprzedni, jest dla danego ciągu liczbą stałą. Więc jeśli mamy pierwszy wyraz i iloraz ciągu, to możemy wyznaczyć kilka początkowych wyrazów tego ciągu.

Ważne!

Jeżeli $(a_{n})$ jest ciągiem geometrycznym o ilorazie $q$ , to dla dowolnej liczby naturalnej $n > 0$ prawdziwa jest równość:

a_{n + 1} = a_{n} \cdot q

Przykład 5

Wyznaczymy wyrazy pięcioelementowego ciągu geometrycznego $(a_{n})$ wiedząc, że jego pierwszy wyraz jest równy $120$ , a iloraz jest równy $0, 5$ .

$a_{1} = 120$

$a_{2} = 120 \cdot 0, 5 = 60$

$a_{3} = 60 \cdot 0, 5 = 30$

$a_{4} = 30 \cdot 0, 5 = 15$

$a_{5} = 15 \cdot 0, 5 = 7, 5$

Odpowiedź:

Szukany ciąg ma postać: $(120; 60; 30; 15; 7, 5)$ .

Znając co najmniej dwa kolejne wyrazy ciągu geometrycznego (niekoniecznie początkowe), można wyznaczyć łatwo iloraz tego ciągu.

Ważne!

Jeżeli $(a_{n})$ jest ciągiem geometrycznym o wyrazach niezerowych, to dla dowolnej liczby naturalnej $n > 0$ prawdziwa jest równość:

\frac{a_{n + 1}}{a_{n}} = q

gdzie:
$q$ – jest ilorazem tego ciągu.

Przykład 6

Wyznaczymy iloraz każdego z podanych ciągów geometrycznych.

$7, 21, 63, 189, . . .$ , $q = \frac{63}{21} = 3$

$- 1, - 2, - 4, - 8, - 16, . . .$ , $q = \frac{- 2}{- 1} = 2$

$. . ., 2 \sqrt{3}, 6, 6 \sqrt{3}, 18, . . .$ , $q = \frac{6 \sqrt{3}}{6} = \sqrt{3}$

Przykład 7

Wiadomo, że trzeci wyraz ciągu geometrycznego $(a_{n})$ jest równy $90$ , a czwarty $270$ obliczymy pierwszy wyraz tego ciągu.

Mamy dane dwa kolejne wyrazy ciągu, zatem możemy obliczyć iloraz tego ciagu.

$a_{3} = 90$

$a_{4} = 270$

$q = \frac{a_{4}}{a_{3}}$

$q = \frac{270}{90} = 3$

Mając trzeci wyraz i iloraz ciągu, można obliczyć drugi wyraz.

$a_{2} = \frac{a_{3}}{q}$

$a_{2} = \frac{90}{3} = 30$

W podobny sposób obliczamy pierwszy wyraz.

$a_{1} = \frac{a_{2}}{q}$

$a_{1} = \frac{30}{3} = 10$

Odpowiedź:

Pierwszy wyraz ciągu $(a_{n})$ jest równy $10$ .

Przykład 8

W ciągu geometrycznym $(b_{n})$ suma dwóch pierwszych wyrazów jest równa $108$ , a różnica wyrazu drugiego i pierwszego jest równa $(- 54)$ . Znajdziemy iloraz tego ciągu.

Oznaczmy:
$b_{1}$ – pierwszy wyraz ciągu,
$b_{2}$ – drugi wyraz ciągu,
$q$ – iloraz ciągu.

Zapisujemy układ równań wynikający z treści zadania.

$\{\begin{cases} b_{1} + b_{2} = 108 \\ b_{2} - b_{1} = - 54 \end{cases}$

Dodajemy stronami równania układu i wyznaczamy $b_{2}$ .

$2 b_{2} = 54$

$b_{2} = 27$

Wyznaczoną liczbę podstwiamy do pierwszego równania i wyznaczamy $b_{1}$ .

$b_{1} = 108 - 27 = 81$

Mamy dwa kolejne wyrazy ciągu – możemy wyznaczyć iloraz ciągu.

$q = \frac{b_{2}}{b_{1}}$

$q = \frac{27}{81} = \frac{1}{3}$

Odpowiedź:

Iloraz ciągu jest równy $\frac{1}{3}$ .

Nie zawsze znamy kilka kolejnych wyrazów ciągu geometrycznego. Ciąg może być też określony wzorem i wtedy potrzebne wielkości możemy wyznaczyć, korzystając ze wzoru.

Przykład 9

Ciąg geometryczny $(a_{n})$ określony jest wzorem $a_{n} = 4 \cdot 5^{n}$ . Znajdziemy iloraz tego ciągu.

Wyznaczamy dwa pierwsze wyrazy ciągu.

$a_{1} = 4 \cdot 5^{1} = 20$

$a_{2} = 4 \cdot 5^{2} = 100$

Obliczamy iloraz ciągu.

$q = \frac{a_{2}}{a_{1}}$

$q = \frac{100}{20} = 5$

Odpowiedź:

Iloraz ciągu jest równy $5$ .

Nie zawsze łatwo jest ustalić, czy ciąg określony za pomocą wyrazów jest ciągiem geometrycznym, czy nie. Na przykład gdybyśmy wzięli pod uwagę tylko pięć początkowych wyrazów ciągu $1, 2, 4, 8, 16, 17, 18, 19, . . .$ , to wydawałoby się, że jest to ciąg geometrycznyciąg geometrycznyciąg geometryczny o ilorazie $2$ . Dlatego znacznie łatwiej jest o sprawdzenie czy ciąg jest geometryczny, mając dany jego wzór.

Ważne!

Ciąg $(a_{n})$ o wyrazach różnych od zera, jest ciągiem geometrycznym, jeżeli dla dowolnej liczny naturalnej $n > 0$ iloraz $\frac{a_{n + 1}}{a_{n}}$ jest stały.

Przykład 10

Sprawdzimy, czy ciąg określony wzorem $a_{n} = 3 \cdot 2^{n}$ jest geometryczny.

Badamy iloraz $\frac{a_{n + 1}}{a_{n}}$ .

$\frac{a_{n + 1}}{a_{n}} = \frac{3 \cdot 2^{n + 1}}{3 \cdot 2^{n}} = \frac{2^{n} \cdot 2}{2^{n}} = 2$

Zauważmy, że wszystkie wyrazy rozpatrywanego ciągu są różne od zera. Stąd i z dowolności liczby $n$ wynika, że ciąg jest geometryczny (wyznaczony iloraz jest stałą liczbą).

Słownik

ciąg geometryczny

ciągiem geometrycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez pomnożenie wyrazu poprzedniego przez liczbę $q$ , zwaną ilorazem ciągu

Wprowadzenie

Film edukacyjny

Słownik