Przeczytaj
Przekrojem bryłyPrzekrojem bryły nazywamy figurę, która jest częścią wspólną bryły i płaszczyzny, która ją przecina.
Przekrojem osiowym bryły obrotowej nazywamy przekrój, który przechodzi przez oś obrotu.
Przekrojem osiowym kuli jest koło wielkie – koło, którego promień jest równy promieniowi kuli. Przekroje zaznaczone w kuli poniżej są przekrojami osiowymi kuli.

Obliczymy pole przekroju zawierającego środek kuli o polu powierzchni .
Rozwiązanie:
Ponieważ jest to przekrój zawierający środek kuli, to jest to koło wielkie. Zauważmy, że pole całkowite kuli wyraża się wzorem , a pole koła wielkiego . To oznacza, że pole koła wielkiego jest czterokrotnie mniejsze od pola całkowitego kuli. A zatem .
Wniosek
Pole przekroju osiowego kuli jest czterokrotnie mniejsze od pola powierzchni kuli.
Pole przekroju osiowegoprzekroju osiowego kuli wynosi . Obliczymy objętość tej kuli.
Rozwiązanie:
Obliczmy promień kuli. Korzystając z pola przekroju osiowego mamy , a stąd .
Obliczamy objętość kuli: .
Jeżeli przetniemy kulę o promieniu płaszczyzną znajdującą się w pewnej odległości (różnej od ) od środka, to otrzymany przekrój również jest kołem. Koło to jest mniejsze od koła wielkiego kuli, a jego odległość od środka spełnia nierówność .

Trójkąt, którego bokami są: – promień kuli, – promień przekroju, – odległość przekroju od środka jest trójkątem prostokątnym tzn.
Obliczymy pole przekroju osiowego kuli o promieniu , którego odległość od środka wynosi .
Rozwiązanie:

Obliczamy promień przekroju z twierdzenia Pitagorasa: . A zatem . Stąd . A zatem pole przekroju wynosi .
Kulę o promieniu przecięto dwiema płaszczyznami równoległymi, tak, że jeden z przekrojów ma promień dwukrotnie dłuższy od drugiego. Obliczymy odległość między tymi przekrojami, jeżeli jeden z nich znajduje się w odległości od środka.
Rozwiązanie:
Obliczamy długość promienia pierwszego z przekrojów z twierdzenia Pitagorasa:

. A zatem .
Ponieważ długość promienia przekroju wynosi , to drugi przekrój musi być mniejszy. Mamy więc . Obliczamy odległość tego przekroju od środkaodległość tego przekroju od środka z twierdzenia Pitagorasa: . Czyli .
Mamy dwie możliwości położenia tego przekroju:

A zatem odległość pomiędzy tymi przekrojami wynosi lub .
Dla zainteresowanych
Przekrój kuli dzieli ją na dwie części, które nazywamy odcinkami kuli.
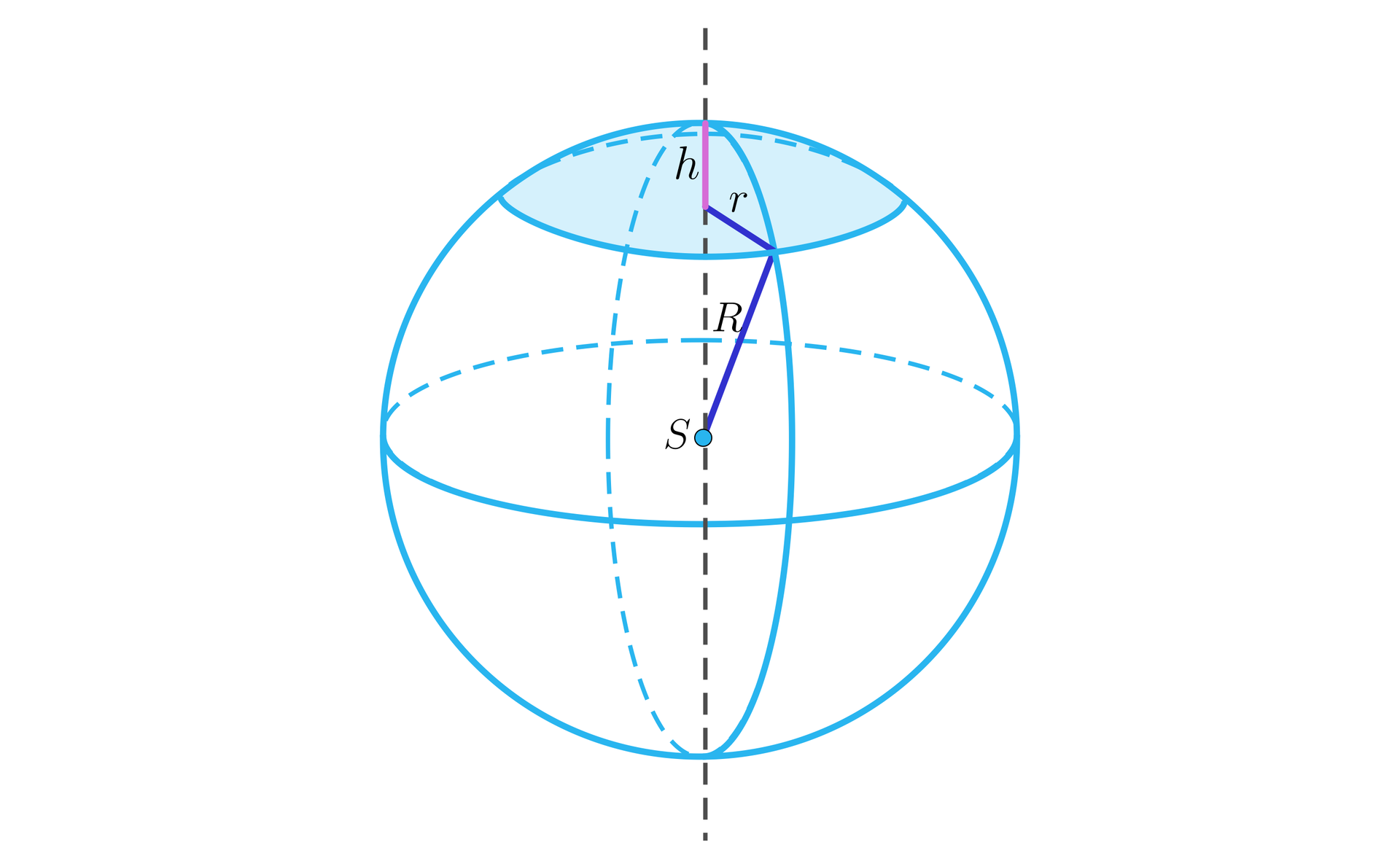
Objętość odcinka kuli policzymy ze wzoru:
Pole powierzchni odcinka kuli policzymy ze wzoru
Oblicz objętość i pole powierzchni mniejszego odcinka kuli powstałego przez przekrój kuli o promieniu oddalonym o od środka.
Rozwiązanie:

Mamy, że . Obliczamy promień przekroju z twierdzenia Pitagorasa: . A stąd .
Mamy więc oraz .
Słownik
część wspólna bryły i płaszczyzny, która ją przecina
przekrój zawierający oś obrotu bryły obrotowej
długość najkrótszego odcinka łączącego środek kuli i przekrój