O pewnej prostej konsekwencji twierdzenia sinusów, która jest potężnym narzędziem w planimetrii

Kolejne zmiany opisu wymagań, jakie szkoła stawia przed absolwentem liceum czy technikum, a które podane są w podstawie programowej, wprowadzają do praktyki lub też eliminują z niej pewne zagadnienia. Dotyczy to m. in. elementów logiki, teorii zbiorów, konstrukcji geometrycznych, ale także pewnego szczególnego twierdzenia z planimetrii, dobrze znanego pod nazwą twierdzenia o dwusiecznej. Jego dowód można przeprowadzić na wiele elementarnych sposobów, ale tutaj pokażemy, że jest ono prostą konsekwencją twierdzenia sinusówsinus kąta w trójkącie prostokątnymsinusów.

o dwusiecznej kąta wewnętrznego w trójkącie

Twierdzenie: o dwusiecznej kąta wewnętrznego w trójkącie

Punkt $D$ jest punktem wspólnym boku $AB$ trójkąta $ABC$ i dwusiecznej kąta wewnętrznego $ACB$, jak na rysunku.

R1XFPxj7Px2yB

Ilustracja przedstawia trójkąt A B C. Z górnego wierzchołka C poprowadzono półprostą, która przecina podstawę A B w punkcie D. Półprosta podzieliła kąt przy wierzchołku C na kąt alfa i drugi kąt. Kąt alfa to kąt D C B.

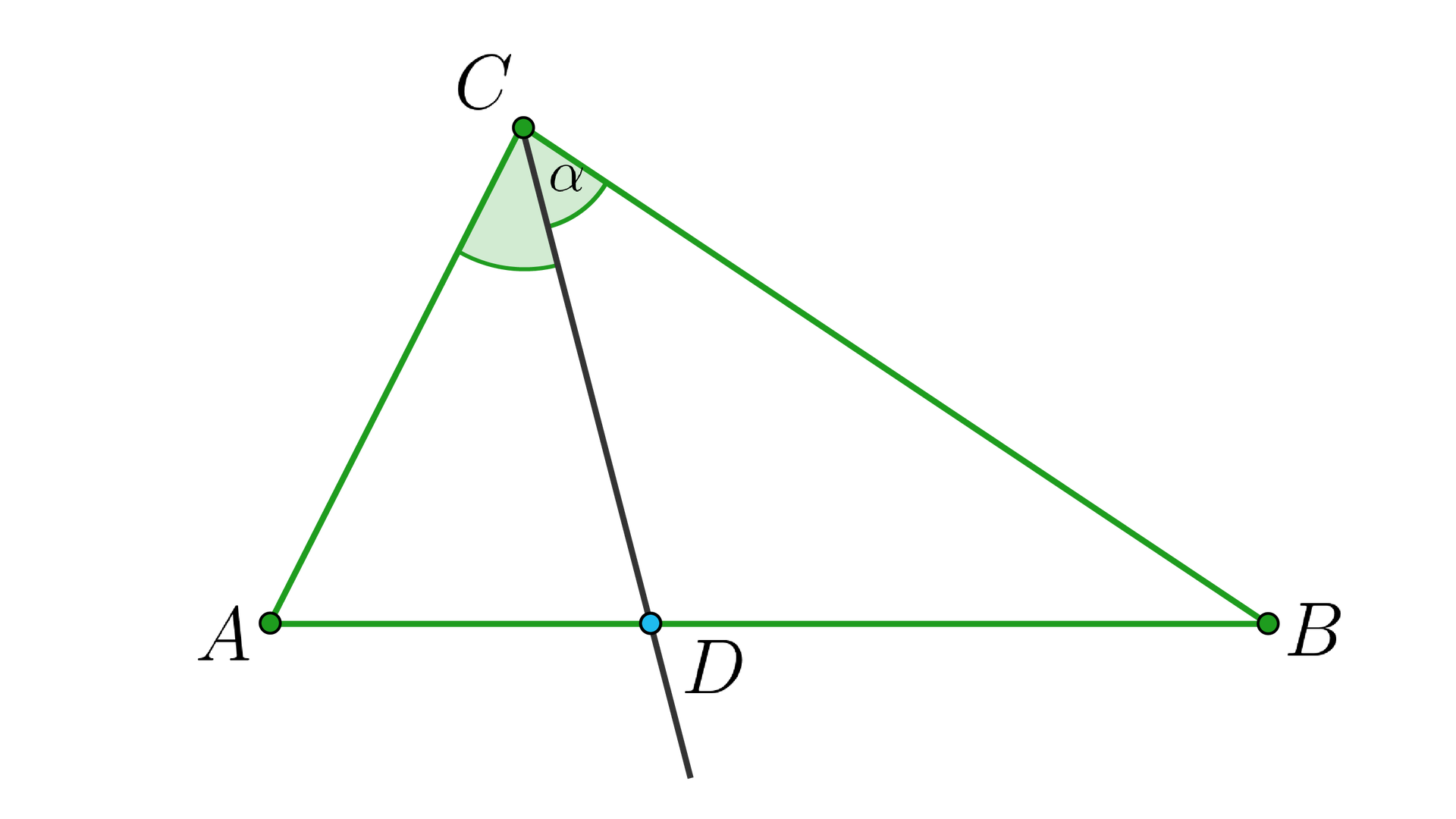
Wtedy $\frac{\left|AD\right|}{\left|AC\right|}=\frac{\left|BD\right|}{\left|BC\right|}$.

Dowód

Zauważmy, że $\left|\sphericalangle BDC\right|=180°-\left|\sphericalangle ADC\right|$, ale $\sin \left(180°-\sphericalangle ADC\right)=\sin \left(\sphericalangle ADC\right)$, zatem $\sin \left(\sphericalangle BDC\right)=\sin \left(\sphericalangle ADC\right)$. Korzystając z twierdzenia sinusów dla trójkąta $ADC$, mamy: $\frac{\left|AD\right|}{\sin \alpha }=\frac{\left|AC\right|}{\sin \left(\sphericalangle ADC\right)}$. Stąd $\sin \left(\sphericalangle ADC\right)=\frac{\left|AC\right|·\sin \alpha }{\left|AD\right|}$.

Analogicznie, korzystając z twierdzenia sinusów dla trójkąta $BDC$ mamy: $\frac{\left|BD\right|}{\sin \alpha }=\frac{\left|BC\right|}{\sin \left(\sphericalangle BDC\right)}$. Stąd $\sin \left(\sphericalangle BDC\right)=\frac{\left|BC\right|·\sin \alpha }{\left|BD\right|}$. Ale $\sin \left(\sphericalangle BDC\right)=\sin \left(\sphericalangle ADC\right)$, zatem $\frac{\left|BC\right|·\sin \alpha }{\left|BD\right|}=\frac{\left|AC\right|·\sin \alpha }{\left|AD\right|}$. Stąd $\frac{\left|AD\right|}{\left|AC\right|}=\frac{\left|BD\right|}{\left|BC\right|}$.

Co należało udowodnić.

Niekiedy, przywołując twierdzenie o dwusiecznej, mówimy krótko, że dwusieczna dzieli przeciwległy bok trójkąta na odcinki proporcjonalne do długości pozostałych boków, przyległych do tych odcinków.

O trygonometrii w trójkącie „niezupełnie prostokątnym”. Czy twierdzenie sinusów jest generatorem nowych twierdzeń, a może tylko automatem do ich dowodzenia?

Model przedstawiony na poniższym rysunku,  jest świetną ilustracją pozwalającą zapisywać zależności między funkcjami trygonometrycznymi kątów dowolnego trójkąta, a także stanowi bazę do dowodzenia wzorów na sumy i różnice funkcji trygonometrycznych, o czym będzie mowa przy okazji trygonometrii. Oczywiście trójkąt może być dowolny („niezupełnie prostokątny”), ale zauważ, że wszystkie zależności są wyprowadzane w trójkątach prostokątnych wyznaczonych przez spodki wysokościspodek wysokości poprowadzonej z wybranego wierzchołka trójkątaspodki wysokości i ortocentrum trójkątaortocentrum trójkątaortocentrum trójkąta.

Rozważmy odcinki w trójkącie wpisanym w okrąg o średnicy $1$. Długości wybranych spośród tych odcinków są podane na rysunku.  

RgYhdM8YejEgz

Ilustracja przedstawia trójkąt A B C. Z górnego wierzchołka C poprowadzono odcinek C S, przy czym koniec S znajduje się na podstawie A B. Z wierzchołka B poprowadzono odcinek B R, gdzie punkt R znajduje się na boku A C. Z wierzchołka A poprowadzono odcinek A Q, gdzie punkt Q znajduje się na boku B C. Odcinki A Q, B R oraz C S przecinają się wewnątrz trójkąta w punkcie O. Przy wierzchołkach oznaczono kąty: przy wierzchołku A kąt alfa, przy B kąt beta, przy C kąt gamma. Na rysunku zapisano następujące zależności: $\left|AB\right|=\sin \gamma$, $\left|AC\right|=\sin \beta$, $\left|BC\right|=\sin \alpha$, $\left|BO\right|=\cos \beta$, $\left|OS\right|=\cos \alpha ·\cos \beta$ oraz $\left|BS\right|=\sin \alpha ·\cos \beta$.

Pokażemy, że rzeczywiście długość odcinka $BC$ jest w przyjętym modelu równa $\sin \alpha$. Rzeczywiście, z twierdzenia sinusów wynika, że $\frac{\left|BC\right|}{\sin \alpha }=2R$. Ale średnica okręgu jest równa $1$, stąd $\frac{\left|BC\right|}{\sin \alpha }=1$. Po wymnożeniu ostatniej równości przez $\sin \alpha$ otrzymujemy, że $\left|BC\right|=\sin \alpha$.

Ostatni wynik oraz zastosowanie definicji funkcji cosinus oraz tangens w trójkącie $BCS$ pozwala wyznaczyć długość odcinków $BS$ oraz $CS$. Mamy $\cos \beta =\frac{\left|BS\right|}{\left|BC\right|}$, stąd $\left|BS\right|=\left|BC\right|·\cos \beta =\sin \alpha ·\cos \beta$. Z kolei $\mathrm{tg}\beta =\frac{\left|CS\right|}{\left|BS\right|}$, stąd $\left|CS\right|=\left|BS\right|·\mathrm{tg}\beta =\sin \alpha ·\cos \beta ·\mathrm{tg}\beta =\sin \alpha ·\sin \beta$.

Wyznaczenie długości odcinka $OS$ wymaga zauważenia równości odpowiednich kątów. Kąt $ACS$ ma miarę $90°-\alpha$, co oznacza, że kąt $COR$ ma miarę $\alpha$. Tak więc kąt $BOS$, jako kąt wierzchołkowy ma tę samą miarę. Możemy więc zapisać, że $\mathrm{tg}\alpha =\frac{\left|BS\right|}{\left|OS\right|}$. Ale $\left|BS\right|=\sin \alpha ·\cos \beta$, zatem $\left|OS\right|=\frac{\sin \alpha ·\cos \beta }{\mathrm{tg}\alpha }=\cos \alpha ·\cos \beta$. Nietrudno zauważyć, że przyjmujemy bez zastrzeżeń fakt, że kąt $\alpha$ nie jest kątem prostym i jego tangens istnieje.

Wyznaczenie długości pozostałych odcinków, które widać na rysunku, jak również tych, które nie zostały zapisane, można, a nawet warto potraktować jako ciekawe ćwiczenie.

A teraz czas na zapisanie przykładowych zależności trygonometrycznych, dla których swoistym generatorem jest powyższy, przedstawiony na rysunku, model.

Zauważmy, że bezpośrednio z nierówności trójkąta, mówiącej o tym, że suma długości dwóch boków trójkąta  jest większa od długości trzeciego boku wynika np., że:

• $\sin \alpha +\sin \beta >\sin \gamma$,

• $\cos \beta +\cos \alpha ·\cos \beta >\sin \alpha ·\sin \beta$.

Bez dodatkowej inwencji można zapisać kolejne tożsamości, korzystając tylko z oznaczeń na rysunku, a jeśli zechcielibyśmy zastosować twierdzenie Pitagorasa, to tych zależności mielibyśmy „odkryć” znacznie więcej.

Na koniec trzeba wspomnieć, że także w przypadku trójkąta rozwartokątnego wpisanego w okrąg o średnicy $1$ długości boków wyrażają się przez sinusy odpowiednich kątów.

Słownik