Ciągiem arytmetycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez dodanie do wyrazu poprzedniego liczby $r$, zwanej różnicą ciągu.

Obliczymy sinusy kątów ostrych trójkąta prostokątnego, którego długości boków tworzą ciąg arytmetyczny.

RJwqDtaoWXxMu

Ilustracja przedstawia trójkąt prostokątny ABC o podstawie a będącej jednocześnie odcinkiem CB przyprostokątnej a dodać r będącej odcinkiem AC oraz przeciwprostokątnej a dodać 2r będącej odcinkiem AB. Przy wierzchołku C oznaczono kąt prosty.

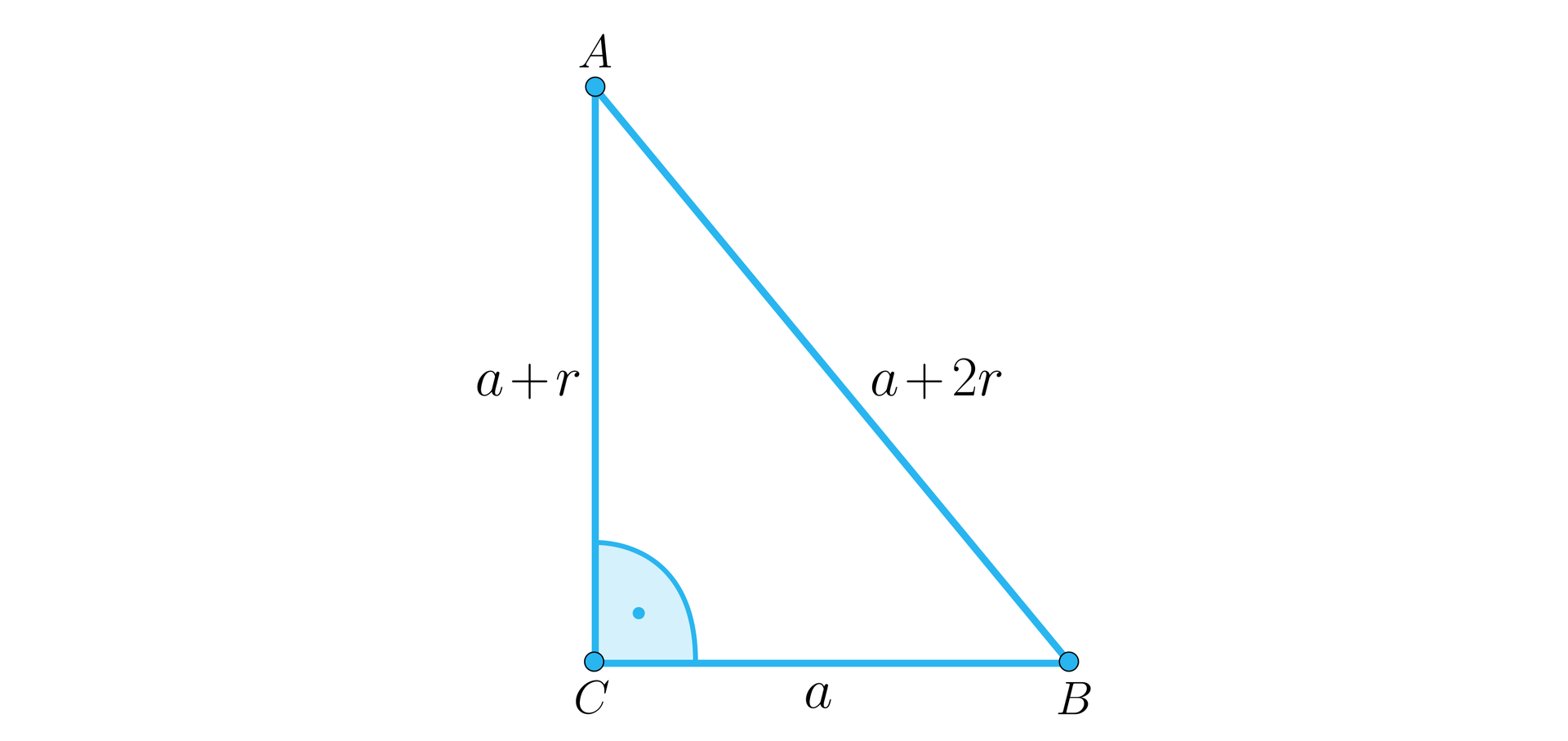
Niech trójkąt $ABC$ będzie rozważanym trójkątem, kąty $CAB$ i $CBA$ niech będą ostre, a kąt $CAB$ – kątem o najmniejszej mierze.

Oznaczmy:
$\alpha$ – miara kąta $CAB$,
$\beta$ – miara kąta $CBA$.

Najmniejszy bok trójkąta, który leży naprzeciw najmniejszego kąta, niech ma długość $a$, gdzie $a>0$.

Natomiast różnica ciągu arytmetycznego, który tworzą długości boków trójkąta, niech będzie równa $r$, gdzie $r>0$.

Wtedy druga przyprostokątna ma długość $a+r$, natomiast przeciwprostokątna ma długość $a+2r$.

Z twierdzenia Pitagorasa wynika, że

$a^2+{\left(a+r\right)}^2={\left(a+2r\right)}^2$

Z otrzymanej równości wyznaczamy $a$.

$a^2+a^2+2ar+r^2=a^2+4ar+4r^2$

$a^2-3ar+ar-3r^2=0$

$a\left(a-3r\right)+r\left(a-3r\right)=0$

$\left(a+r\right)\left(a-3r\right)=0$

$a=-r$ – sprzeczność, bo $a>0$

$a=3r$

Wyznaczamy sinusy katów ostrych trójkąta $ABC$.

$\sin \beta =\frac{a+r}{a+2r}=\frac{3r+r}{3r+2r}=\frac{4r}{5r}=0,8$

$\sin \alpha =\frac{a}{a+2r}=\frac{3r}{3r+2r}=\frac{3r}{5r}=0,6$

Odpowiedź:

Sinusy kątów ostrych trójkąta są równe odpowiednio $0,8$ i $0,6$.

Dany jest trójkąt $ABC$ taki, że $\left|AB\right|<\left|AC\right|<\left|BC\right|$.

Wykażemy, że gdy długości boków tego trójkąta tworzą ciąg arytmetyczny, to promień koła wpisanego w ten trójkąt jest równy trzeciej części wysokości opuszczonej na bok $AC$.

R1F4TV3xGRNWl

Ilustracja przedstawia trójkąt ABC o podstawie a dodać r będącej jednocześnie odcinkiem AC oraz o bokach a będącym odcinkiem AB oraz a dodać 2r będącym odcinkiem BC. Z górnego wierzchołka B upuszczono wysokość h i oznaczono miedzy nią a podstawą kąt prosty.

Oznaczmy:
$r$ – różnica ciągu arytmetycznego,
$R$ – promień koła wpisanego w trójkąt,
$\left|AB\right|=a$,
$\left|AC\right|=a+r$,
$\left|BC\right|=a+2r$,
$h$ – wysokość trójkąta poprowadzona do boku $AC$.

Korzystamy ze wzoru na pole trójkąta o bokach danej długości i promieniu koła wpisanego w ten trójkąt oraz ze wzoru na pole trójkąta o danej podstawie i wysokości opuszczonej na tę podstawę.

$P=\frac{\left|AB\right|+\left|AC\right|+\left|BC\right|}{2}\cdot R$

$\frac{1}{2}(a+r)\cdot h=\frac{a+a+r+a+2r}{2}\cdot R$

Przekształcamy zapisaną równość, z której wyznaczamy $R$.

$\frac{1}{2}(a+r)\cdot h=\frac{a+a+r+a+2r}{2}\cdot R|\cdot 2$

$(a+r)\cdot h=(3a+3r)\cdot R$

$R=\frac{(a+r)\cdot h}{3(a+r)}$

$R=\frac{h}{3}$

Z zapisanej równości wynika, że promień koła wpisanego w trójkąt $ABC$ jest równy trzeciej części wysokości poprowadzonej do boku $AC$, co należało wykazać.

Miary kątów wielokąta wypukłego tworzą ciąg arytmetyczny o różnicy $10°$. Najmniejszy kąt tego wielokąta ma miarę $100°$. Ustalimy, ile boków ma ten wielokąt.

Suma kątów wielokąta o $n$–bokach jest równa $\left(n-2\right)·180°$, a każdy z kątów wielokąta ma miarę mniejszą od $180°$.

Z drugiej strony wiemy, że miary kątów wielokąta stanowią wyrazy ciągu arytmetycznego, stąd ich suma jest równa

$\frac{100°+100°+\left(n-1\right)·10°}{2}·n$

Porównujemy otrzymane wyrażenia.

$\left(n-2\right)·180°=\frac{100°+100°+\left(n-1\right)·10°}{2}·n$

Sprowadzamy otrzymane równanie do najprostszej postaci.

$\left(n-2\right)·360°=\left(200°+10°·n-10°\right)·n$

$360°·n-720°=10°n^2+190°·n$

$n^2-17n+72=0$

Rozwiązujemy równanie kwadratowe.

$∆=289-288=1$

$n=\frac{17-1}{2}=8$ lub $n=\frac{17+1}{2}=9$

Dla $n=8$ największy kąt wielokąta ma miarę $100°+70°=170°$.

Dla $n=9$ największy kąt wielokąta ma miarę $100°+80°=180°$ – otrzymujemy sprzeczność (bo miara kąta wielokąta wypukłego jest mniejsza od $180°$).

Odpowiedź:

Wielokąt ma $8$ boków.

Długości krawędzi prostopadłościanu wychodzące z jednego wierzchołka tworzą ciąg arytmetycznyciąg arytmetycznyciąg arytmetyczny o różnicy $2$. Wysokość prostopadłościanu jest najdłuższą krawędzią. Pole podstawy prostopadłościanu wynosi $24$. Obliczymy pole powierzchni bocznej tego prostopadłościanu.

Oznaczmy:
$a$, $a+2$ – długości krawędzi podstawy prostopadłościanu.

Podstawą prostopadłościanu jest prostokąt o polu $a\left(a+2\right)$. Zatem

$a\left(a+2\right)=24$

$a^2+2a-24=0$

Rozwiązujemy otrzymane równanie kwadratowe.

$∆=4+96=100$

$a=\frac{-2-10}{2}=-6$ – nie spełnia warunków zadania, bo $a>0$

$a=\frac{-2+10}{2}=4$

Obliczamy długości krawędzi prostopadłościanu.

$4+2=6$

$6+2=8$

Teraz możemy obliczyć pole powierzchni bocznej prostopadłościanu.

$P=2·6·8+2·4·8=160$

Odpowiedź:

Pole powierzchni bocznej prostopadłościanu jest równe $160$.

Czworokąt $ABCD$ opisany jest na okręgu. Długości trzech kolejnych boków czworokąta tworzą ciąg arytmetyczny. Udowodnimy, że przynajmniej dwa boki tego czworokąta mają tę samą długość.

RE0dAUo8lonZT

Ilustracja przedstawia czworokąt ABCD opisany na okręgu. Boki tego czworokąta są następujące: a jest jednocześnie odcinkiem AD, x jest jednocześnie odcinkiem DC, a dodać 2r jest jednocześnie odcinkiem CB, a dodać r jest jednocześnie odcinkiem BA.

Oznaczmy:
$a$ – długość najkrótszego boku czworokąta,
$r$ – różnica ciągu, który tworzą długości boków czworokąta,
$x$ – długość boku czworokąta, który nie tworzy z pozostałymi ciągu arytmetycznego.

Czworokąt jest opisany na okręgu, zatem sumy długości przeciwległych boków są równe.

$a+r+x=a+a+2r$

Zatem

$x=a+r$

Wynika stąd, że $\left|DC\right|=\left|AB\right|$, czyli dwa boki czworokąta mają tę samą długość.

Zauważmy, że gdy $r=0$, to wszystkie boki czworokąta są równe.

ciągiem arytmetycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez dodanie do wyrazu poprzedniego liczby $r$, zwanej różnicą ciągu