Przeczytaj

Już wiesz

Proste o równaniach w postaci kierunkowej $y = a_{1} x + b_{1}$ oraz $y = a_{2} x + b_{2}$ są prostopadłe, gdy zachodzi warunek: $a_{1} \cdot a_{2} = - 1$ (czyli, gdy ich współczynniki kierunkowe są przeciwne i odwrotne).

RKq1RSDfH4TVw

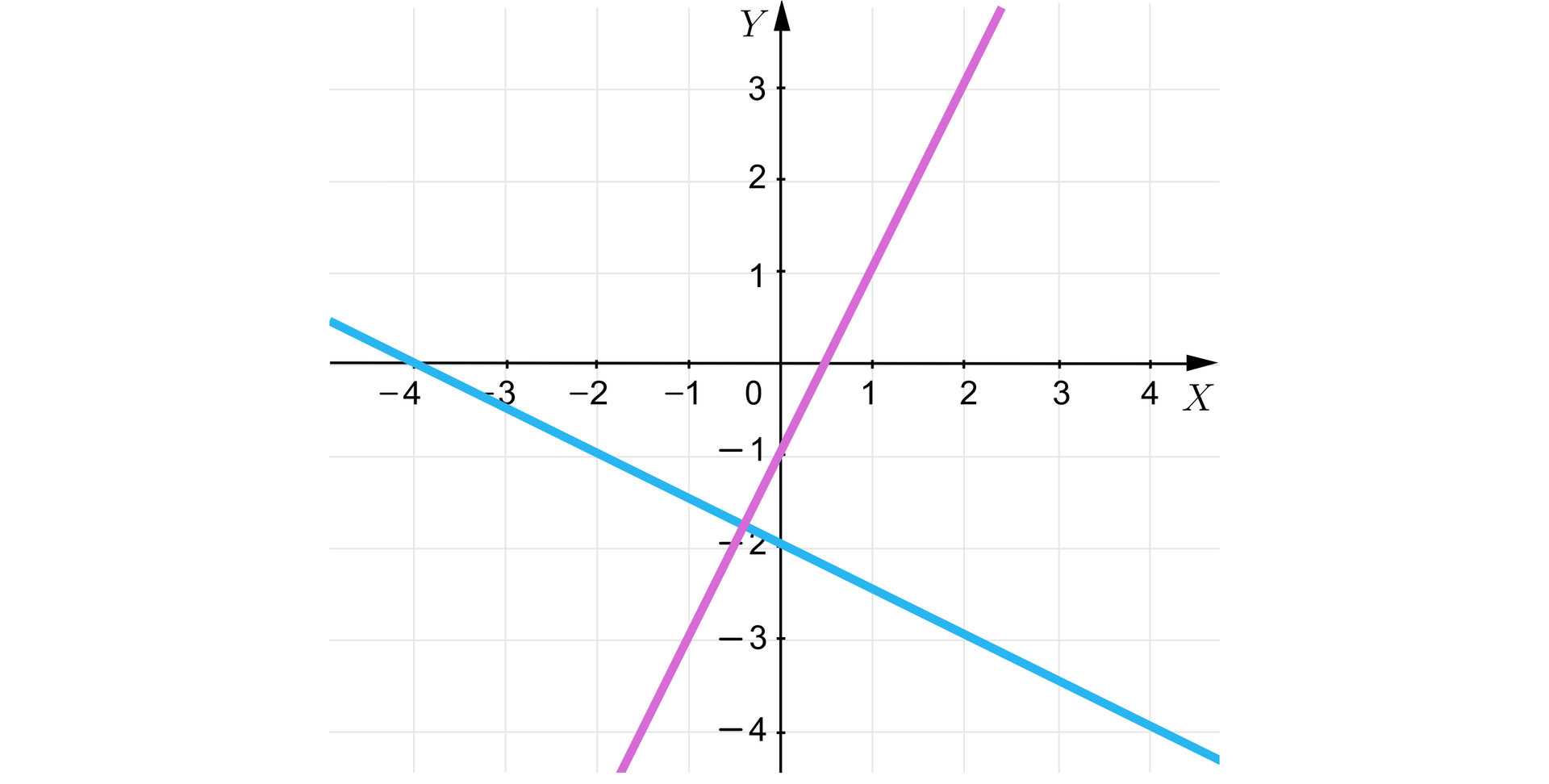
Rysunek przedstawia układ współrzędnych z poziomą osią X od minus czterech do czterech oraz z pionową osią Y od minus czterech do trzech. Na płaszczyźnie narysowano dwie prostopadłe do siebie proste.

Ważne!

Dla dowolnej prostej $y$ i dowolnego punktu $A$ istnieje dokładnie jedna prosta przechodząca przez punkt $A$ i prostopadła do prostej $y$ .

równanie ogólne prostej

Definicja: równanie ogólne prostej

Równanie $A x + B y + C = 0$ nazywamy równaniem ogólnym prostej, gdy $A$ i $B$ nie są jednocześnie równe $0$ .

warunek prostopadłości prostych

Twierdzenie: warunek prostopadłości prostych

Proste o równaniach w postaci ogólnej $A_{1} x + B_{1} y + C_{1} = 0$ oraz $A_{2} x + B_{2} y + C_{2} = 0$ są prostopadłe, gdy zachodzi warunek:

$A_{1} A_{2} + B_{1} B_{2} = 0$ .

Dowód

Przekształcimy równania ogólne dwóch prostych $A_{1} x + B_{1} y + C_{1} = 0$ oraz $A_{2} x + B_{2} y + C_{2} = 0$ do postaci kierunkowej.

Otrzymujemy następujące równania kierunkowe prostych: $y = - \frac{A_{1}}{B_{1}} x - \frac{C_{1}}{B_{1}}$ oraz $y = - \frac{A_{2}}{B_{2}} x - \frac{C_{2}}{B_{2}}$ .

Wiemy, że dwie proste zadane równaniem kierunkowym są prostopadłe, gdy ich współczynniki kierunkowe są przeciwne i odwrotne.

Zatem otrzymujemy równanie: $- \frac{A_{1}}{B_{1}} \cdot (- \frac{A_{2}}{B_{2}}) = - 1$ , co po przekształceniu daje szukany warunek $A_{1} A_{2} + B_{1} B_{2} = 0$ .

Ważne!

Proste o równaniach ogólnych $A_{1} x + C_{1} = 0$ i $B_{1} y + C_{1} = 0$ są zawsze prostopadłe, gdy $A_{1} \neq 0$ i $B_{1} \neq 0$ .

Przykład 1

Sprawdzimy, czy proste o równaniach $3 x + y - 5 = 0$ oraz $- x + 3 y + 4 = 0$ są prostopadłe.

Otrzymujemy dane: $A_{1} = 3$ , $A_{2} = - 1$ , $B_{1} = 1$ oraz $B_{2} = 3$ .

Podstawiamy do równania $A_{1} A_{2} + B_{1} B_{2} = 0$ .

Otrzymujemy, że $3 \cdot (- 1) + 1 \cdot 3 = 0$ .

Równanie jest spełnione, zatem proste o podanych równaniach są prostopadłe.

Przykład 2

Wyznaczymy, dla jakiej wartości parametru $m$ proste o równaniach $3 x + (2 - m) y + 1 = 0$ oraz $(2 + m) x - 4 y - 3 = 0$ są prostopadłe.

Otrzymujemy dane: $A_{1} = 3$ , $A_{2} = 2 + m$ , $B_{1} = 2 - m$ , $B_{2} = - 4$ .

Podstawiamy do równania $A_{1} A_{2} + B_{1} B_{2} = 0$ .

Otrzymujemy równanie: $3 (2 + m) + (2 - m) \cdot (- 4) = 0$ .

Równanie jest spełnione dla $m = \frac{2}{7}$ i dla takiej wartości parametru $m$ zadane proste są prostopadłe.

Przykład 3

Wyznaczymy, dla jakiej wartości parametru $a$ proste o równaniach $- 4 x + y - 3 = 0$ oraz $y = a x + 1$ są prostopadłe.

Przekształcimy drugie równanie do postaci ogólnej: $a x - y + 1 = 0$ .

Otrzymujemy dane: $A_{1} = - 4$ , $B_{1} = 1$ , $A_{2} = a$ , $B_{2} = - 1$ .

Podstawiając do równania $A_{1} A_{2} + B_{1} B_{2} = 0$ otrzymujemy, że $- 4 a - 1 = 0$ , zatem $a = - \frac{1}{4}$ .

Zadane proste są prostopadłe dla $a = - \frac{1}{4}$ .

Przykład 4

Wyznaczymy równanie ogólne prostej prostopadłej do prostej o równaniu $2 x - y + 5 = 0$ , przechodzącej przez punkt $A = (1, 2)$ .

Prostą w postaci ogólnej oznaczymy jako $A_{2} x + B_{2} y + C_{2} = 0$ .

Wykorzystamy warunek prostopadłościwarunek prostopadłości prostychwarunek prostopadłości $A_{1} A_{2} + B_{1} B_{2} = 0$ .

Otrzymujemy dane: $A_{1} = 2$ i $B_{1} = - 1$ .

Po podstawieniu do warunku prostopadłości otrzymujemy, że $2 A_{2} - B_{2} = 0$ .

Przekształcając to równanie otrzymujemy: $- \frac{A_{2}}{B_{2}} = - \frac{1}{2}$ .

Korzystając z dowodu twierdzenia o warunku prostopadłości prostych zauważmy, że jest to wartość współczynnika kierunkowego $a$ dla prostej $y = a x + b$ .

Zatem prosta prostopadła jest postaci $y = - \frac{1}{2} x + b$ .

Jeżeli do równania prostej prostopadłej podstawimy punkt $A = (1, 2)$ , to otrzymujemy, że $b = \frac{5}{2}$ .

Stąd szukana prosta ma postać ogólną $x + 2 y - 5 = 0$ .

Przykład 5

Wyznaczymy równanie prostej, która przecina oś $X$ w punkcie o odciętej $2$ , prostopadłej do prostej $x - 3 y + 1 = 0$ .

Prosta prostopadła ma równanie $A_{2} x + B_{2} y + C_{2} = 0$ .

Wykorzystamy warunek $A_{1} A_{2} + B_{1} B_{2} = 0$ .

Mamy, że $A_{1} = 1$ , $B_{1} = - 3$ .

Po podstawieniu do równania otrzymujemy, że $A_{2} - 3 B_{2} = 0$ , więc współczynnik kierunkowy $a = - \frac{A_{2}}{B_{2}} = - 3$ .

Szukana prosta prostopadła ma postać $y = - 3 x + b$ .

Ponieważ prosta przecina oś $X$ w punkcie o odciętej $2$ , zatem do wyznaczenia wartości $b$ rozwiązujemy równanie:

$0 = - 3 \cdot 2 + b$ , czyli $b = 6$ .

Prosta w postaci kierunkowej opisana jest za pomocą równania $y = - 3 x + 6$ , co po przekształceniu do postaci ogólnej jest równoważne równaniu prostej $3 x + y - 6 = 0$ .

Słownik

warunek prostopadłości prostych

proste $A_{1} x + B_{1} y + C_{1} = 0$ oraz $A_{2} x + B_{2} y + C_{2} = 0$ są prostopadłe, gdy $A_{1} A_{2} + B_{1} B_{2} = 0$

Wprowadzenie

Film samouczek

Słownik