Słowniczek
Liczby w mnożeniu mają swoje nazwy.
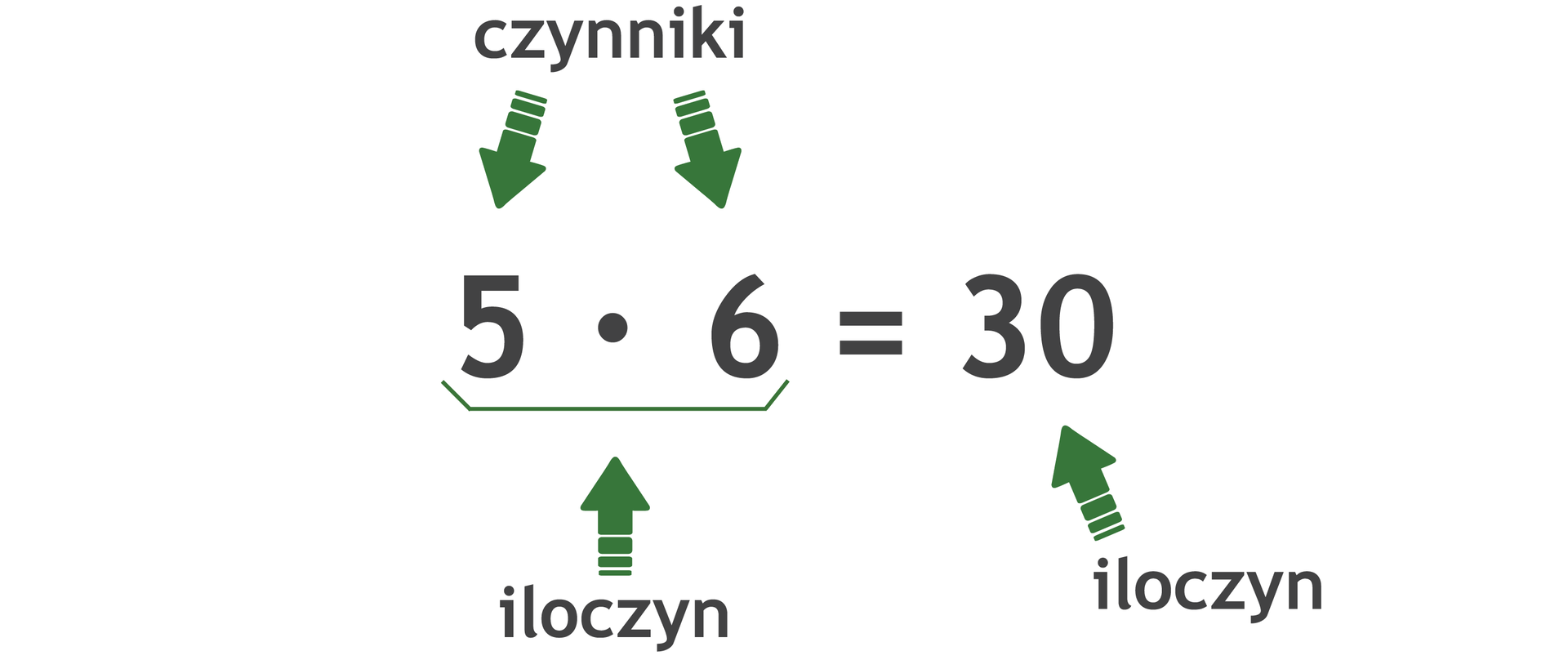
Liczby występujące w dzieleniu mają swoje nazwy.

Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.
Działania wykonujemy w następującej kolejności:
najpierw wykonujemy działania w nawiasach,
następnie mnożenie lub dzielenie,
na końcu dodawanie lub odejmowanie.
Kołem o środku w punkcie i promieniu nazywamy figurę zbudowaną ze wszystkich punktów płaszczyzny, których odległość od punktu jest mniejsza bądź równa promieniowi.

Film dostępny na portalu epodreczniki.pl
Animacja
Liczby mieszane składają się z części całkowitej i części ułamkowej.
Na przykład

Liczby naturalne to: , , , , , , , , , , , , , …, , …, , , …, , … .
Do zapisu liczb naturalnych służą cyfry: , , , , , , , , i nazywane cyframi arabskimi.
Wykonując dodawanie kilku liczb, można dowolnie łączyć po dwa sąsiadujące składniki, a suma nie ulegnie zmianie.
Mówimy, że dodawanie jest łączne.
Wykonując mnożenie kilku liczb, można dowolnie łączyć dwa sąsiadujące czynniki, a iloczyn nie ulegnie zmianie. Mówimy, że mnożenie jest łączne.
Suma długości wszystkich boków kwadratu to jego obwód.

Suma długości wszystkich boków prostokąta to jego obwód.

Liczby występujące w odejmowaniu mają swoje nazwy.

Okręgiem nazywamy figurę złożoną ze wszystkich punktów płaszczyzny równo oddalonych od ustalonego punktu, zwanego środkiem okręgu.

Film dostępny na portalu epodreczniki.pl
Animacja
Oś liczbowa to prosta, na której zaznaczamy
zwrot (strzałkę wskazującą, w którą stronę liczby się zwiększają)
liczbę
liczbę
R16n4mokZxkqa1 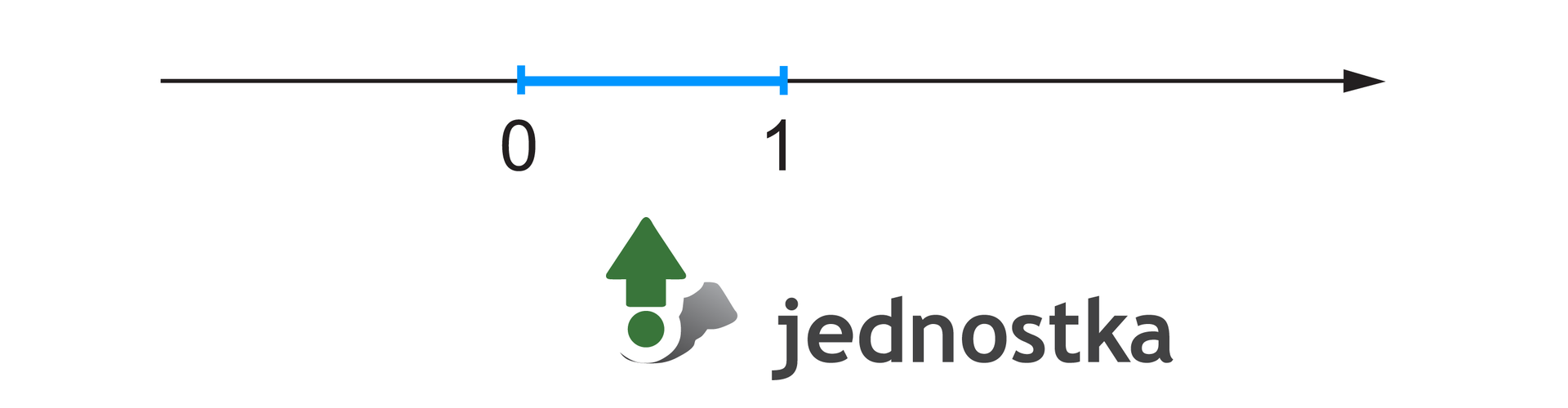 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Punkty odpowiadające liczbom i są końcami odcinka, który nazywamy jednostką osi liczbowej.
Długość odcinka jednostkowego wynosi .
Dowolny punkt leżący na prostej dzieli tę prostą na dwie części. Każdą z tych części nazywamy półprostą. Każda półprosta ma początek, ale nie ma końca. Początkiem półprostej jest punkt dzielący prostą.

Odcinek łączący środek okręgu z punktem leżącym na okręgu, nazywamy promieniem okręgu.
Oznaczamy go najczęściej małą literą r.

W dodawaniu można zmieniać kolejność składników, a suma nie ulegnie zmianie. Mówimy, że dodawanie jest przemienne.
W mnożeniu możemy zamienić kolejność czynników, a wynik nie ulegnie zmianie. Mówimy, że mnożenie jest przemienne.
Jeśli pomnożymy licznik i mianownik ułamka przez tę samą liczbę, różną od zera, to mówimy, że rozszerzyliśmy ułamek, a wartość ułamka się nie zmieni.
Liczby występujące w dodawaniu mają swoje nazwy:

Jeśli licznik i mianownik ułamka podzielimy przez tę samą liczbę, różną od zera, to wartość ułamka nie zmieni się. Mówimy, że skróciliśmy ułamek.
Na przykład
Skracając ułamek przez , otrzymujemy .
Prostopadłościan, którego wszystkie krawędzie są równe to sześcian. Każda ściana sześcianu jest kwadratem.
Ułamek, którego mianownik jest liczbą nazywamy ułamkiem dziesiętnym.
Ułamek, którego nie można skrócić nazywamy ułamkiem nieskracalnym.
Wierzchołkiem kąta nazywamy wspólny początek obu półprostych, a każdą z półprostych nazywamy ramieniem kąta.
Gdy masę danego przedmiotu podajemy z użyciem dwóch jednostek (mian), to mówimy, że zapisaliśmy masę za pomocą wyrażenia dwumianowanego, np. .



Podobnie postępujemy, gdy zaokrąglamy liczby do pełnych dziesiątek tysięcy, setek tysięcy itd.
Aby zaokrąglić liczbę z dokładnością do określonego rzędu, należy zwrócić uwagę na cyfrę z rzędu o niższego. Jeśli tą cyfrą jest lub , to zaokrąglamy w dół, jeśli jest lub to w górę.