Sprawdź się
W trójkącie , w którym , , odcinki, na jakie dwusieczna kąta wewnętrznego podzieliła bok różnią się o . Oblicz obwód tego trójkąta.
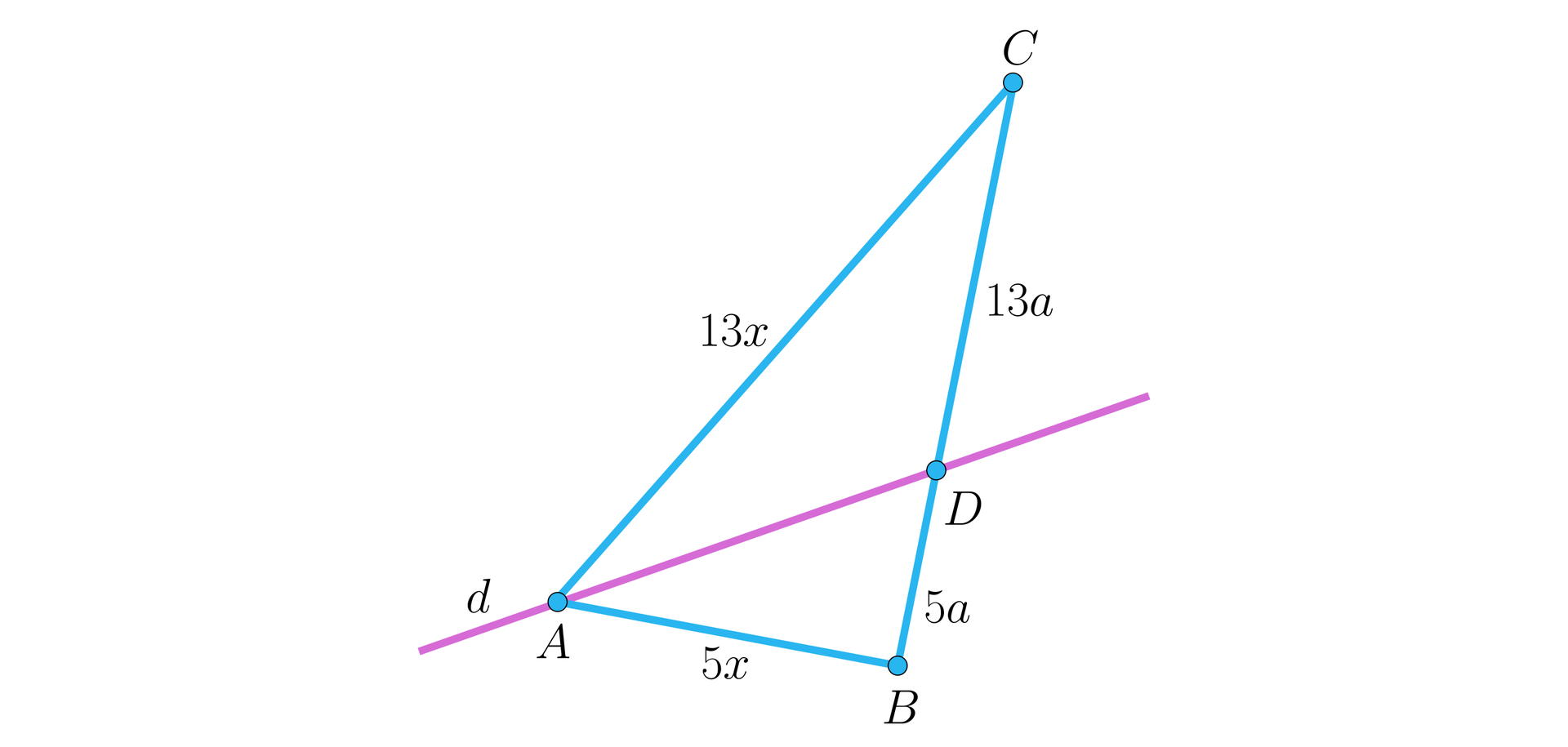
Dany jest trójkąt , w którym długości boków są liczbami całkowitymi. Dwusieczna kąta zewnętrznego przy wierzchołku przecięła prostą w punkcie , jak na rysunku. Oblicz długości boków trójkąta, jeżeli: oraz .

Dwusieczna kąta ostrego w trójkącie prostokątnym podzieliła przyprostokątną w stosunku . Wyznacz sinusy kątów ostrych tego trójkąta.
Dany jest trójkąt , w którym , , . Długości odcinków i , na jakie dwusieczna kąta podzieliła bok są odpowiednio równe: Możliwe odpowiedzi: 1. , , 2. , , 3. , , 4. ,
Zaznacz poprawną odpowiedź. Dany jest trójkąt , w którym , , . Długości odcinków i , na jakie dwusieczna kąta podzieliła bok są odpowiednio równe:
- ,
- ,
- ,
- ,
W trójkącie o obwodzie odcinki, na jakie dwusieczna kąta wewnętrznego podzieliła bok są odpowiednio równe: , . Oblicz długości boków trójkąta.
Zaznacz poprawną odpowiedź. Dany jest trójkąt , w którym dwa boki mają odpowiednio długości i . Dwusieczna kąta wewnętrznego podzieliła trzeci bok trójkąta na dwa odcinki, z których jeden ma długość równą . Trzeci bok tego trójkąta ma długość:
Dany jest trójkąt , o bokach długości , , , jak na rysunku.
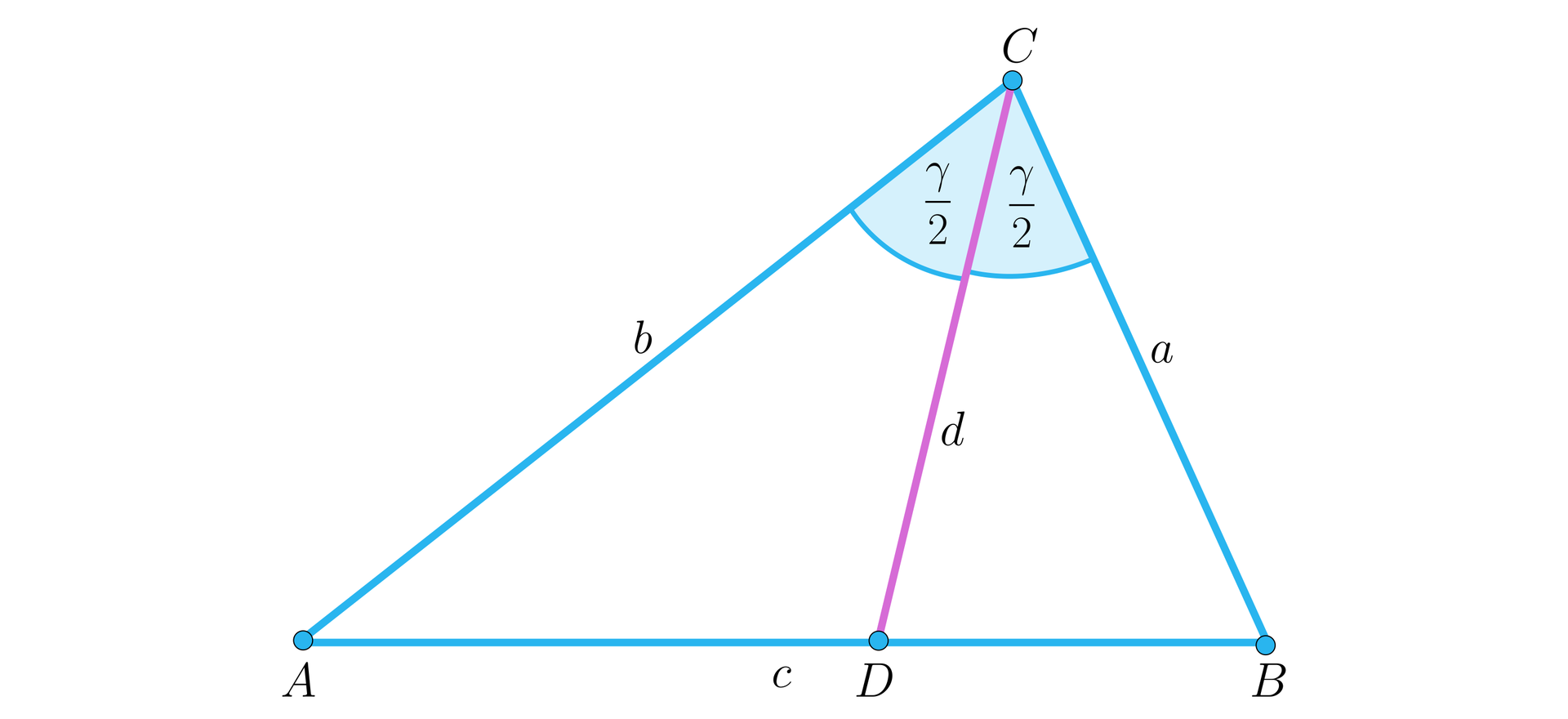
Zapoznaj się z następującycm twierdzeniem:
Długość odcinka dwusiecznej kąta wewnętrznego trójkąta jest równa
.
Dowód: Elementy do uszeregowania: 1. Najpierw dla trójkąta mamy: , zatem ., 2. Podstawiając teraz obliczoną wcześniej długość odcinka otrzymujemy: ., 3. A korzystając ze wzoru skróconego mnożenia możemy zapisać, że ., 4. Redukując wyrazy podobne i wyłączając wspólny czynnik przed nawias dostajemy: ., 5. Teraz dwukrotnie skorzystamy z twierdzenia cosinusów., 6. Zacznijmy od zastosowania twierdzenia o dwusiecznej kąta wewnętrznego. Wtedy mamy, że: ., 7. Stąd , co należało wykazać., 8. Wykorzystując wyznaczoną wartość cosinusa możemy zapisać odpowiednią równość dla trójkąta : ., 9. Stąd ., 10. Po doprowadzeniu do wspólnego mianownika otrzymujemy, że
., 11. Pozostaje przekształcić wyrażenie: .
Stąd 1. , 2. , 3. , 4. .
Teraz dwukrotnie skorzystamy z twierdzenia cosinusów.
Najpierw dla trójkąta mamy: , zatem 1. , 2. , 3. , 4. .
Wykorzystując wyznaczoną wartość cosinusa możemy zapisać odpowiednią równość dla trójkąta : .
Podstawiając teraz obliczoną wcześniej długość odcinka otrzymujemy: .
Pozostaje przekształcić wyrażenie: .
Po doprowadzeniu do wspólnego mianownika otrzymujemy, że
.
Redukując wyrazy podobne i wyłączając wspólny czynnik przed nawias dostajemy: 1. , 2. , 3. , 4. .
A korzystając ze wzoru skróconego mnożenia możemy zapisać, że .
Stąd 1. , 2. , 3. , 4. , co należało wykazać.